探求向量数量积最值问题的求解方法

魏 燕

(浙江金华第一中学)

求向量数量积的最大值与最小值是高考中的热点问题,经常与平面向量的模与夹角等知识综合考查,题型多种多样,其中与几何图形相结合的综合题比较常见.由于部分学生对各类题型缺乏科学的练习和系统的整理,遇到此类问题感觉会无从下手.为此,本文介绍了探求向量数量积最值问题的几种方法,供读者参考.

1 巧设动点

在一些题目中,已知动点是某条已知曲线上的点(这实际上是给出的一个重要条件),通过巧妙设出动点,往往可以找到问题的切入点.

如图1所示,以AB所在的直线为x轴、AB的垂直平分线为y轴建立平面直角坐标系,则A(－1,0),B(1,0),C(－1,－2),又点P在单位圆x2＋y2＝1(y≥0)上运动,所以设P(cosθ,sinθ).

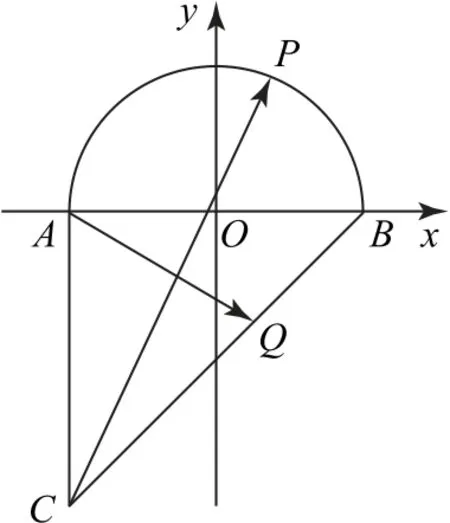
图1

图2

图3

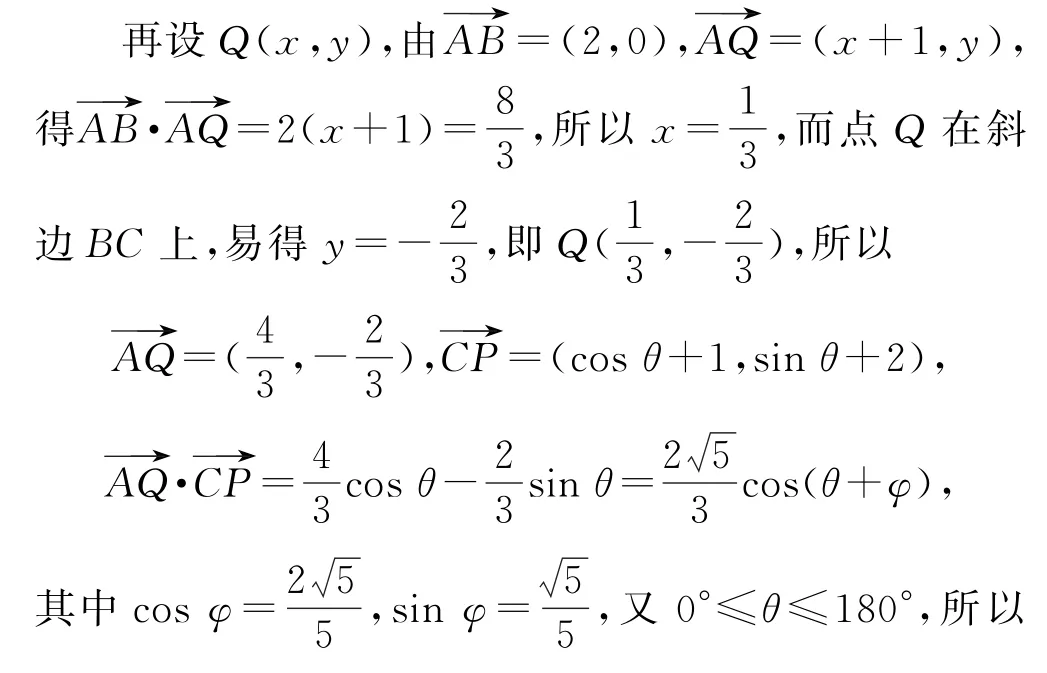
与圆有关的最值问题,一般是将圆心设为坐标原点,这样圆上的动点就可以用圆心角表示,为后面利用三角函数的有界性解题创造条件.

2 抓住范围

在解决问题的过程中,经常会遇到一些用参数表示的条件,挖掘并巧妙地利用这些参数的变化范围也是求向量数量积最值问题的常用方法.

在此解法中,利用参数λ构建了向量数量积的函数f(λ),然后由参数的范围确定了函数的值域,这样也就顺利求出向量数量积的最大值了.

3 几何分析

在探究一些几何图形中的向量问题时,要善于抓住其特点,如中点、平行、比例关系等,这往往就是解题的突破口.

4 引参助解

在求向量数量积的最值问题时,可以适时地引入参数,用参数将一些变化中的向量表示出来,然后便能运用代数的方法求解最值问题.

例4 如图4 所示,在Rt△ABC中,AB＝AC,BC＝4,O为BC的中点,以O为圆心、1 为 半 径 的 半 圆 与BC交于点D,P__为半圆上任意一点,求的最小值.

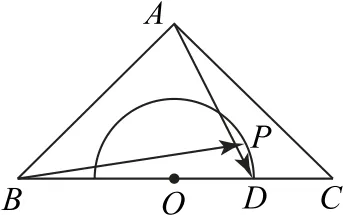
图4

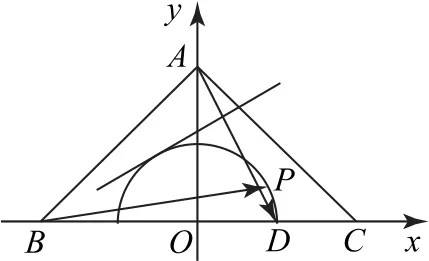
图5

在此解法中,通过引入参数t,将待求的向量数量积转化为一条直线,而需求的最值就是直线与半圆相切的特殊情况下的取值.

5 代数运算

在解决向量数量积最值问题时,有时会用到二次函数、三角函数、基本不等式等知识求解.

例5 如图6 所示,在△ABC中,D,E分别是AB,AC的中点,M是直线DE上的动点.若△ABC的面积为2,求2的最小值.

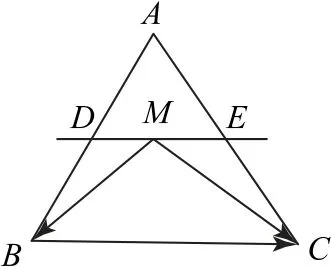
图6

因为D,E分别是AB,AC的中点,所以点M到BC的距离是点A到BC的距离的一半,又△ABC的面积为2,所以S△MBC＝1.

此解法用一个角将所求的向量数量积表示出来,这是解决问题的关键.

(完)