例谈三角函数中初相φ 的求解策略
——基于核心素养的高三复习微专题
王中学 何 虎
(安徽省合肥一六八中学)
三角函数是高中数学重要内容,也是高考的必考考点,高考主要考查学生对三角函数基本性质的掌握程度,因此备受高考命题者的青睐.但由于三角函数具备单调性、对称性、周期性、最值等多种性质,特点鲜明,部分同学对其理解与转化存在一定的困难.根据三角函数的性质求解析式中的初相φ的值或取值范围是三角函数中比较典型的一类问题,本文以近几年的高考题及模拟题为例,立足于三角函数的性质,对三角函数中初相φ的求解策略进行归纳总结.
1 与函数的对称性有关
1.1 对称轴


1.2 对称中心(或零点)
例3 (2020年新高考Ⅰ卷10,多选题)图1是函数y=sin(ωx+φ)的 部 分 图 像,则sin(ωx+φ)=( ).

图1

图2


综上,选BC.

函数f(x)=Asin(ωx+φ)(A>0,ω>0)是由函数y=Asinμ和μ=ωx+φ复合而成的,把正弦函数y=sinx的对称中心(kπ,0)以及对称轴)进行整体代换即可,形如函数y=Asinωx(A≠0,ω≠0)的函数为奇函数,关于(0,0)对称;形如y=Acosωx(A≠0,ω≠0)的函数为偶函数,关于y轴对称;在进行变换时,也可以用诱导公式进行变换,而符号不影响函数的奇偶性.
2 与函数值有关
例4 (2022年全国乙卷理15)记函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)的最小正周期为T,若为f(x)的零点,则ω的最小值为__________.因为f(x)=cos(ωx+φ)(ω>0,0<φ<π),所以f(x)的最小正周期为,而

方法2 因为函数f(x)的最大值为2,所以sin(x+φ)=cosx=1,解得x=2kπ(k∈Z),则

方法3 因为函数f(x)的最大值为2,而(cosx)max=1,因此只需要把sin(x+φ)转化为cosx即可.



求解时,将一些已知点(最高点、最低点或“零点”)的坐标代入解析式,再结合图形求解φ.若对φ的范围有要求,则可写出φ所满足的一般式,对其所有的取值进行验证,使其符合要求.
3 与函数的单调性有关




4 与ω 的取值有关

例10 已知函数f(x)=Asin(ωx+φ)图像的一部分如图3 所示,求函数f(x)的解析式.

图3
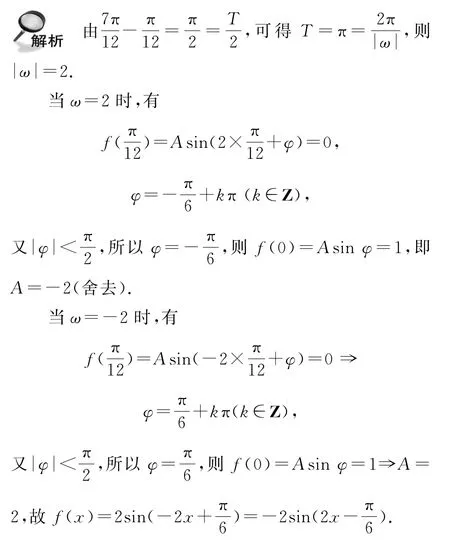

ω的取值情况会影响初相φ值的确定,由ω的取值得出初相φ的表达式,然后可根据函数的性质,如单调性、对称性、最值点、零点、函数值等最终确定初相φ的取值.
5 小结
通常三角函数中的初相φ的变化是由函数图像的左右平移产生的,函数的单调区间、对称轴、对称中心、最值点等性质会随着图像左右平移有所变化.但无论题目的背景换成什么,其本质不变,都是通过正弦函数、余弦函数、正切函数的图像和性质来解决.因此,借助三角函数的性质求解三角函数解析式中的初相φ,应在熟悉三角函数图像的基础上,通过掌握初相φ与三角函数的单调性、对称性和最值等之间的密切联系,利用转化与化归、数形结合等数学思想,把复杂问题简单化、熟悉化.三角函数具有几何和代数的双重特征,命题专家往往利用它来考查学生的分析和解决问题能力,只有抓住概念的本质,把数学思想方法贯穿于教学中,才能提高学生的思维水平,培养解题能力与数学学科素养,从而适应考试题目的创新.
(完)

