一题多解提能力 一题多变探本质——以2023年全国甲卷第16题“爪型”三角形为例

邓成兵 冉茂园

(1.四川省成都市航天中学校 2.重庆鲁能巴蜀中学)

“爪型”三角形是指在给定的一个三角形中,连接一个顶点和对边上的任意一点(除端点外)构成的图形.“爪型”三角形问题主要考查数学建模、数学运算和逻辑推理等数学核心素养.2021年高考数学试题中的解三角形题型出现了“爪型”三角形.随着高考命题的不断发展,分线由原来的中线逐步演变为角平分线、高线或一般分线(如表1).

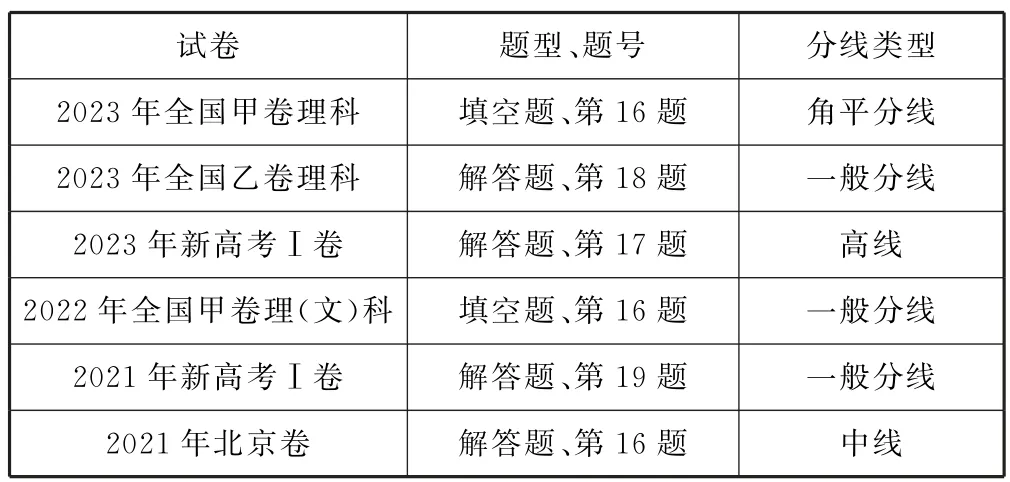
表1 2021—2023年高考数学全国卷“爪型”三角形统计

因此,笔者从“爪型”三角形的代数特征和几何特征出发,寻求比较简捷的解题方法,总结解题规律,从整体上认识和把握“爪型”三角形问题,解题时做到有的放矢.希望通过对2023年全国甲卷理科第16题的解题策略进行探究,得到一般性的结论、研究路径和方法,对大家的复习备考有所帮助.

1 试题呈现与解法探究

题目 (2023 年全国甲卷理16)在△ABC中,∠BAC＝60°,AB＝2,BC＝6,∠BAC角平分线交BC于点D,则AD＝_________.

分析 本题是典型的“爪型”三角形问题,需要灵活应用正余弦定理进行边角互化,进而求角平分线的长度,多维度考查学生的数学运算、数据分析、逻辑推理等数学核心素养,综合性较强.

1.1 题之一问,问之一解

解法1 待定系数法、正弦定理

设AD＝2m,过点D作DF⊥AC于点F,如图1所示.由正弦定理可得

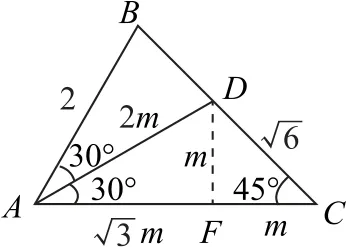
图1

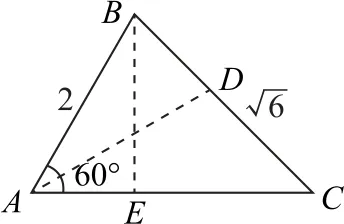
图2

故m＝1,所以AD＝2m＝2.

解法2 作高保角、正弦定理

解法3 余弦定理、等面积法

由余弦定理可得

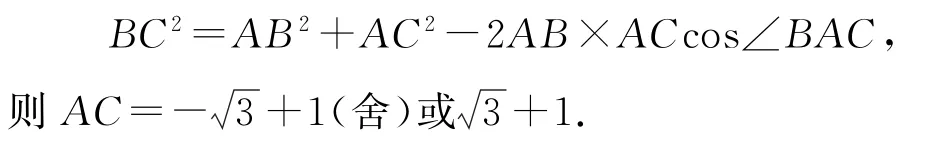
设AD＝x,由等面积法可得

所以

化简求得AD＝2.解法1利用“待定系数法、正弦定理、直角三角形”求解.解法2 利用“作高保角、余弦定理”求解.这种方法也是求解高中三角函数、立体几何问题的重要方法,但学生很难想到作BE⊥AC,这种方法对学生的思维要求比较高.解法3利用“余弦定理、等面积法”求解.这是解斜三角形的核心,学生更容易入手.另外,如果再结合几何图形进行思考,就更容易使问题获解.

在新教材、新课标和新高考(简称三新)背景下,为了让数学的解题方法思路更清晰有序,且能够高效精准地将高中数学题目涉及的知识点与自己大脑系统中已有的相关知识体系建立一个恰当有效的联系.笔者认为借助思维导图(如图3)呈现思维过程,可以让同学们更直观地理解不同解法的切入点和优缺点.著名数学家波利亚说过这样一句话:“掌握数学也就意味着要善于解题,”所以解一道经典的数学题不能只就题论题,更重要的是要揭开此题的内涵和价值.为实现这一目的,需要对它不断进行变式及归纳,通过题之一问、问之一解、解之一变、变之一通、通之一悟、悟之一类的解题策略,对经典的高考试题探索多种题型转变的一般规律,揭示其本质特征,从而帮助学生更有效地学习数学.现对上题中式①进行再探究,得到“爪型”三角形的一般性结论.

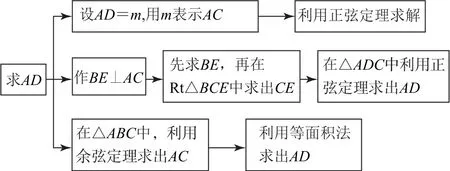
图3

1.2 解之一变、变之一通

例1 若点D为BC边上异于B,C两端点的任意一点,如图4所示,设∠BAD＝α,∠CAD＝β,AB＝c,AC＝b,所以∠BAC＝α＋β,则

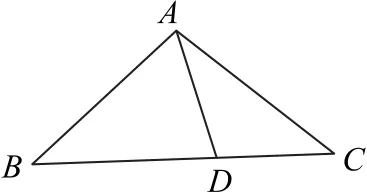
图4

在三角形中出现了边和角的正弦,有效的途径是利用三角形面积第二公式进行求解,即

因为S△ABC＝S△ABD＋S△ACD,所以

两边同时除以bc×AD,化简可得

结论1 在△ABC中,∠A的平分线与BC边相交于点D,设∠BAD＝∠CAD＝θ,则∠BAC＝2θ,代入例1的式①化简得

即已知两边及夹角可求角平分线长,把这个公式叫“爪型”三角形的角平分线公式.下面用结论1求解前面的问题.

解法4 结论应用

在△ABC中,由余弦定理得

1.3 通之一悟、悟之一类

结论2 在△ABC中,D为BC的中点,借助上述式③整理化简可得

把此式称为“爪型”三角形的中线公式,将之变形可得2019年人教A 版«必修第二册»第53 页第15 题的结论

即已知三角形三边可求中线长.

变式2 如 图5 所示,在△ABC中,∠BAC＝60°,AB＝2,AC＝＋1,D为BC靠近点B的三等分点,则AD2＝_________.

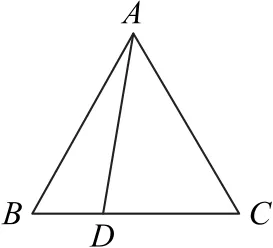
图5

则

把变式2中式①变为一般情况,我们可以获得什么样的结论呢?

如图6所示,若D为线段BC上的一动点,满足BD∶DC＝m∶n,可以获得“爪型”三角形向量的一般性结论.

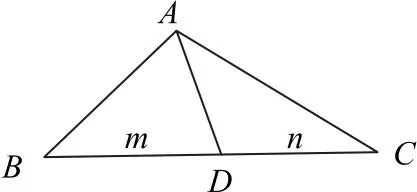
图6

结论3 在△ABC中,若D为线段BC上的一动点,满足BD∶DC＝m∶n,则

变 式 3 在 △ABC中,∠BAC＝60°,AB＝2,AC＝3＋1,AD⊥BC交BC于点D,如图7所示,则AD2＝_______.

图7

将把变式3的两边及夹角一般化,我们可以获得什么结论呢?

结论4 在△ABC中,∠BAC＝θ,AB＝c,AC＝b,BC＝a,AD⊥BC交BC为点D,如图8所示,则

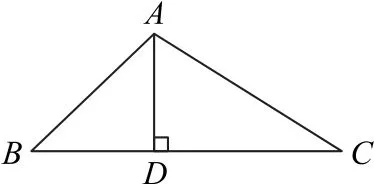
图8

即已知两边及夹角可求高线长.

在△ABC中,由余弦定理可得

,代入式①中化简可得

2 链接高考,迁移经验

笔者通过对一道高考题的解法及变式进行探究,获得了有关“爪型”三角形的中线公式、角平分线公式、高线公式及向量中“爪型”三角形结论.当然,这些结论也能用于求解对应的高考试题.

例2 如图9所示,在△ABC中,已知∠BAC＝的平分线AD与BC边相交于点D,AD＝2,则AB＋AC的最小值为_________.

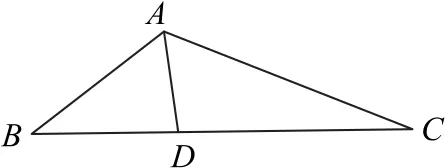
图9

由“爪型”三角形的角平分线公式可得

例3 (2023年新高考Ⅱ卷17,节选)记△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为,D为BC的中点,且AD＝1.若b2＋c2＝8,求b,c.

如图10所示,在△ABC中,由“爪型”三角形的中线长公式得

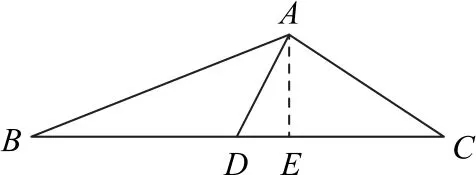
图10

即4＋a2＝2(b2＋c2)＝16,则

例4 (2021年新高考Ⅰ卷19)记△ABC的内角A,B,C的对边分别为a,b,c.已知b2＝ac,点D在边AC上,BDsin∠ABC＝asinC.

(1)证明:BD＝b;

(2)若AD＝2DC,求cos∠ABC.

(1)证明过程略.

(2)在△ABC中,平方得

由余弦定理得

联立①②得11b2＝3c2＋6a2,因为b2＝ac,所以3c2－11ac＋6a2＝0,所以c＝3a或.

在△ABC中,由余弦定理可得

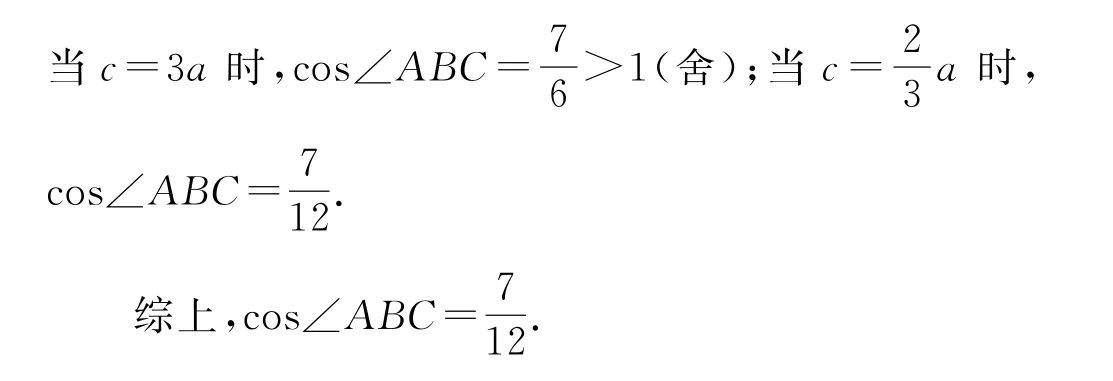
3 解题反思

本文从不同的角度对2021—2023 年数学高考“爪型”三角形进行了深入探究,归纳出“爪型”三角形的中线、角平分线、高线及“爪型”三角形向量的一般表达式并对其进行证明,运用了特殊到一般、化归与转化、函数与方程等思想.“爪型”三角形在高考试卷中难度属于中等,解这类三角形方法很多,通常可以采用“邻补角”“算两次”策略,依据正弦定理和余弦定理列方程求解,也可以采用作高、作平行线等手段利用初等几何知识求解,亦可借助向量工具,采用基底法进行求解.如果运用本文总结的“爪型”三角形的四条性质求解,不但可以简化运算,还可以提高做题的效率及正确率.此外,通过一题多解到一题多变的训练,可以拓宽和深化解题思路,提高解题技巧和分析问题、解决问题能力,激发学生探究数学问题的热情.

从以上的分析可以看出,此题目蕴含着多么丰富和深刻的数学思想方法,教师要对教材上经典的例题、习题和高考真题进行认真的探究,做到一题多解、一题多变,才能深入挖掘其内在的规律、探究到更一般的结论,从而由最初的授人以鱼(基于课本教知识)过渡到授之以渔(基于知识教方法),最后实现悟其渔识(基于方法教思想)的转变.

(完)