初中数学动态几何问题常用解题方法探究

刘丽丽

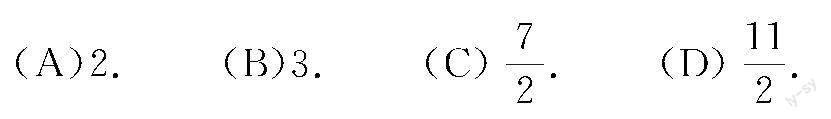
【摘要】动态几何问题作为中考的重点题型，也是学生失分的重灾区.本文结合实际情况，针对性地提出解答动态几何问题常用的几种方法，借助函数性质、图形性质、图形关系及数形结合，并结合例题进行练习，以帮助学生快速掌握并在实际答题中灵活运用.

【关键词】动态几何；初中数学；解题方法

动态问题是初中阶段几何知识的重要题型之一，在中考中经常出现，这类问题通常比较复杂，不仅考查学生的计算能力，还需要学生拥有较强的抽象思维.虽然在授课过程中教师会将其作为一类重点题型进行讲解，但是在实际的调查中发现，学生对于动态问题依旧心存畏惧，诸多学生在面对动态几何问题时直接选择放弃，一些学生面对问题没有思路，无从下手，导致这类问题严重影响了学生的数学成绩，因此，本文将系统性地总结解答动态几何问题常用的方法，为学生提供参考.

1 借助函数性质求

在动态几何问题中，最值问题是最为常见的，在面对这类问题时，学生便可以尝试采用函数法来解题，结合函数的性质得到最终答案.借助函数解题的关键在于能够正确找到题目中各种量之间的关系，设出参数，而后根据关系列出对应的一次函数、二次函数及反比例函数，进而借助其性质得到答案.在借助函数解答问题时，需要注意自变量的取值范围，否则计算容易出现错误.

例1 如图1，矩形ABCD，AB=10cm，AD=6cm，E，F為动点，分别沿AD，DC方向以1cm/s，2cm/s的速度进行运动，当运动ts后S△DEF+S△ABE存在最大值，则t为（  ）

解析 根据题意可以得到DF=2AE，根据已知条件，设出AE长度后，便可以得到两个三角形面积与AE之间的关系，整理则成了关于AE的二次函数最值问题.需要注意的是因为AE在AD上运动，所以0

设AE长为x，

2 借助图形性质

借助图形的基本性质解答动态问题也是常用的一种方法，在解答问题时，可以灵活运用等边三角形、正方形、菱形、圆等诸多基础图形的性质，来解答动态问题.但是运用这种方法解题时，需要学生拥有较强的图形思维及抽象思维，同时要熟练掌握各种图形的诸多性质，结合题目中图象运动过程中的定量与变量，从而解答问题.

例2 如图2，直角坐标系中，A（12，0），B（0，9），过点O且与AB相切的圆交x，y轴于P，Q，则PQ最短为（  ）

解析 仔细阅读题目可以发现，无论圆处于什么位置，始终与AB相切，且∠QOP=90°，结合圆的性质可得当PQ经过圆心，即为圆的直径时取的最小值，则本题便可快速解答.

3 借助图形关系

在解答动态几何问题时，通常可以通过角度、线段之间的关系，借助三角形相似、全等、线段平行等诸多知识，来解答问题.有时需要学生根据题意，作出相应的辅助线，帮助解题，而这也是学生所面临的最大困难，因此学生需要熟练掌握图象的基本性质，通过题意快速作出有利于解题的辅助线，进而解答问题.

例3 如图3，直角坐标系中，A（3，4），C（x，0），且－2

解析 根据题目，需要确定tanα的值，而要想确定其最大值，则需要将其转化到三角形中，此时可以进一步将其转化为求解BG的最大值，而要求BG最大值，则需要借助相似三角形进行求解.

过A作x轴，AH⊥x=－2的垂线，垂足分别为F，H，

因为y轴平行于直线x=－2，

又因为AH=3+2=5，

因为BC⊥AC，

则∠BCO+∠CBG=90°，

∠BCO+∠ACF=90°，

所以∠CBG=∠ACF，

所以△BGC∽△CFA.

设BG=y，

则CF=3－x，CG=x+2，

4 结语

综上所述，只要能够系统性地分析、总结初中动态几何问题，可以发现，借助以上几种策略能够解决大多数的问题.因此，在实际的学习中，学生应当多加练习，熟练掌握每一种解题方法，根据题意，快速选择与之相对应的解题策略，如此，在考试中遇到相关题目便会迎刃而解.