二次函数动点问题常见题型解法探究

张伟

【摘要】二次函数是初中阶段学生数学知识体系中的重要构成，以其为基础的相关题型也丰富多变，其中动点问题既是考试的重点内容，也是学生失分的重灾区.本文总结二次函数动点问题中常见的面积问题、线段问题、三角形问题及相似图形问题相关解题策略，供学生参考，以提高学生的解题效率.

【关键词】动点问题；二次函数；解题

在对学生二次函数知识的考查中，往往会融合其他知识，以达到对学生综合能力考查的目的.而在诸多题型中，动点问题无疑是重要的一类，同时也是学生较为惧怕的一类.动点问题不仅考查学生对二次函数、图形知识的掌握及计算能力，还考查了学生的抽象思维等学科素养.二次函数动点问题是因函数图象上移动的点所引发的，题型也是复杂多变，因此学生对这一问题的掌握并不理想，在考试中错误率较高.因此，本文系统性地总结了二次函数动点问题的常见题型及解题策略，以促进学生对知识的掌握.

1 面积问题

面积问题是二次函数动点知识考查中最为常见的一个题型，是对学生二次函数及图形知识的综合考查，同时也要注意动点的取值范围，而后根据相关条件建立关系便可进一步解答.在解答面积问题时，学生需具备较强的空间思维能力及计算能力，把握动点的运动对图象的影响，如此便可快速解答问题.

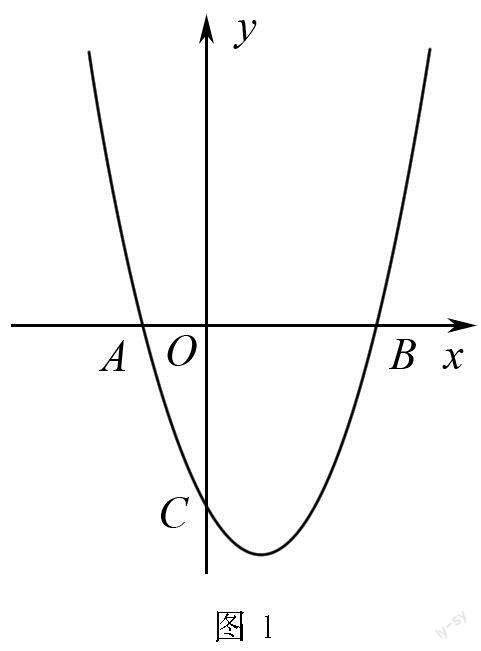
例1 如图1，抛物线y=x2+bx+c与x轴交于点A（－1，0），B（3，0），与y轴交于点C，

（1）求抛物线解析式；

（2）若D为抛物线一点，且S△ABD=2S△ABC，求D坐标.

解 （1）将点A（－1，0），B（3，0）坐标代入y=x2+bx+c，

可解得b=－2，c=－3，

则抛物线的解析式为y=x2－2x－3.

（2）因為△ABD与△ABC拥有共同的边AB，

故要想S△ABD=2S△ABC，仅需其AB边上的高比值为2，

因为D在抛物线上，

所以设其为D（m，m2－2m－3），

因为y=x2－2x－3，将x=0代入，

可得C点坐标为（0，－3），

即m2－2m－3=6，

求出m便可得D点坐标.

2 线段问题

二次函数中动点线段问题总体可以分为两类，即一个动点和两个动点.无论哪一类问题，题目中都大概率会涉及到二次函数以外的其他函数，故在解答这类问题时，学生要灵活运用函数相关的知识，将线段长短问题转化为一个二次函数的表达式，而后结合题目中的信息进行解答.

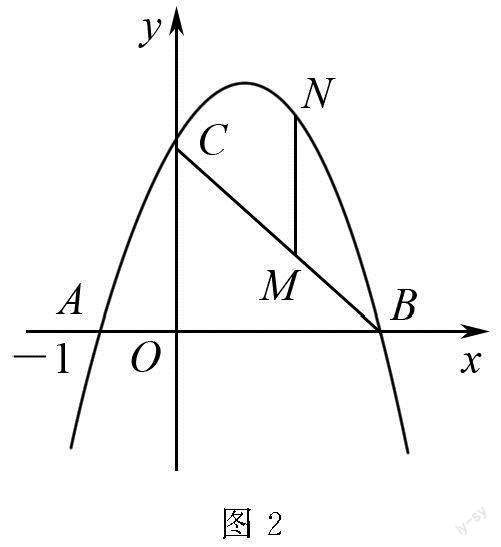
例2 如图2，点N为抛物线y=－x2+2x+3上一动点，且在线段BC上方，BC上有一动点M，若MN∥y轴，则MN的最值为多少？

解析 因为抛物线y=－x2+2x+3，

可得B（3，0），C（0，3），

则线段BC的解析式为y=－x+3，

因M在线段BC上，

则设其坐标为（m，－m+3），

因N为y=－x2+2x+3上动点，

则设其坐标为（m，－m2+2m+3），

当MN∥y轴时，MN的长度则为二者纵坐标的差，

设MN的长度为函数LMN，

则LMN=（－m2+2m+3）－（－m+3）=－m2+3m，

整理可得LMN=－（m－1.5）2+2.25，

可知函数LMN为开口向下的二次函数，故MN最大值为2.25，无最小值.

3 三角形问题

在解答二次函数中动点引起的三角形问题时，重点并不在于函数，而是需要学生掌握三角形相关的各种知识，以此结合二次函数进行分析，联立求解，便可得到答案.

例3 如图3，二次函数交坐标轴于A（－1，0），B（4，0），C（0，－4）三点，P为直线BC下方抛物线上一动点.

（1）求二次函数解析式；

（2）是否存在点P，使△POC是以OC为底的等腰三角形，求其坐标.

解 （1）设函数解析式为y=ax2+bx+c，

将A（－1，0），B（4，0），C（0，－4）三点代入，

可解得a=1，b=－3，c=－4，

故函数解析式为y=x2－3x－4.

（2）因△POC是以OC为底的等腰三角形，则P点应位于OC的垂直平分线上，

因为OC=4，故点P的纵坐标为-2，

因为点P在抛物线上，则可将y=－2代入到解析式中，

则有x2－3x－4=－2，同时，因其在直线BC下方，故应舍去小于0的根，

4 结语

综上所述，本文系统性地总结了二次函数动点问题中常见的面积问题、线段问题、三角形问题及相似图形问题，并对其进行了实际的讲解.总体来说，学生要想解答这类问题，首先要对二次函数、一次函数、三角形、多边形等基础知识有一个完整的认识，在此基础之上熟练掌握各种题型的解题原理、过程，如此便可快速解答相关问题.

参考文献：

[1]李惠平.二次函数动点问题的教学设计[J].数理天地（初中版），2022（03）：77-78.

[2]胡雅雯.二次函数中动点图形的面积最值问题探究[J].中学数学，2022（22）：36-38.

[3]王伟.二次函数面积有关题型分析[J].数理化学习（初中版），2021（12）：15-16.

[4]王珍.探讨初中数学二次函数动点问题的教学策略[J].中学数学，2021（20）：64-65.