高中数学章节复习课的教学设计——以“解三角形”为例

⦿ 安徽省界首中学 关广严

数学复习课教学的开展,可使学生的基础知识得到进一步巩固,同时也可有效完善学生的知识结构.就高中数学实际课堂教学模式来看,往往存在诸多不足,如维持学生学习热情难度高,学生学习缺少主动性,未足够重视学生数学思维以及思想方法的培养;等等.可见,强化章节复习课教学活动的设计十分重要,可进一步提升高中数学章节复习课教学效率.

1 夯实学生基本知识技能

复习课的主要目标是为了夯实学生基础知识、基本技能的掌握情况,同时促进学生问题解决能力的进一步提升.复习课对学生理论知识的学习具有积极促进作用,同时也可强化学生对基础知识的理解,帮助学生进行系统、全面的知识回顾以及整理,实现系统化知识网络的构建.在此基础上,教师还需进行思想方法的渗透,不断给予学生启发,帮助学生更好地掌握数学的本质特征,不断夯实基本数学技能,灵活应用基础知识以及思想方法解决问题.

以“解三角形”章节知识为例,夯实学生基本知识、基本技能的关键就是正弦定理、余弦定理以及三角形面积等的综合应用.具体设计如下.

1.1 第一课时

课前测评:已知△ABC为钝角三角形,其中AB=2,AC=5,BC=x,求x的取值范围.

学习过程:

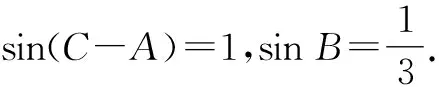
(1)求sinA的值;

(1)求tanC的值;

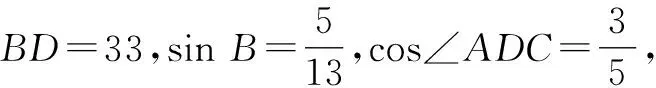
1.2 第二课时

课前测评:已知a,b,c为△ABC的内角A,B,C的对边,且acosC+ccosA=2bcosB,求角B的大小.

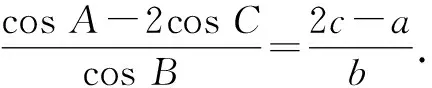
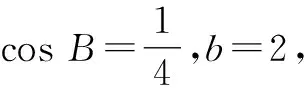
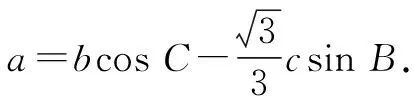
(1)求角B的大小;

(2)若D为边AC的中点,AB=2,BC=1,求△ABC面积的最大值.

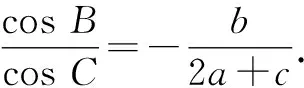
(1)求角B的大小;

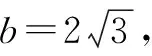
2 进一步完善学生数学认知结构

数学学科具有较强的抽象性、逻辑性以及严谨性.在高中数学章节复习课中,可引导学生围绕知识展开复习整理,从而形成结构化知识体系,促进学生整体结构化认知的进一步锻炼与提高.在实际发展学生学习能力的过程中,离不开科学、合理的复习课程的设计,同时也需要教师为学生提供积极且有效的引导.教师需要遵循教学原则选择教学策略,合理开展复习课教学设计工作,从而在最大程度上完善学生的数学认知结构.

回归解三角形问题的本质,借助平面向量的综合应用来分析与处理对应的解三角形问题,可以进一步完善学生的数学认知结构.具体设计如下.

(2)若b2+c2=8,求b,c.

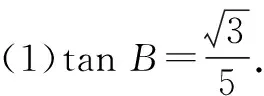
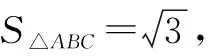
结合D为BC的中点,可求出b=c=2.

3 提高学生综合思维能力

在开展数学知识章节系统复习的过程中,首先需要帮助学生打破知识点之间的割裂认识情况,探寻各个知识点之间的结构联系;其次应探寻结构联系所形成的知识板块,围绕知识点展开综合延伸,从而促进知识网状结构的形成;最后应贯通知识块与知识网之间的联系,从整体角度进行知识的思考与应用.章节系统复习过程中应遵照循序渐进的原则,可在各个阶段内逐步提升学生整体性综合思维能力.

在实际解三角形问题中,往往离不开相应的三角函数知识,涉及解三角形与三角恒等变换的综合应用问题就显得尤为重要.具体设计如下.

3.1 第一课时

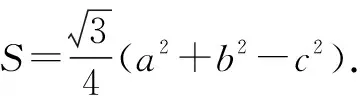
(1)求sinB;

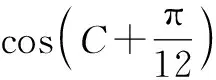
(1)求f(x)的表达式;

(2)在△ABC中,当f(C)=1,且2sin 2B=cosB+cos(A-C),求sinA的值.

3.2 第二课时

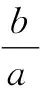
学习过程:在△ABC中,已知(a+b+c)(b+c-a)=bc,求角A的大小.

当堂检测:在△ABC中,角A,B,C分别与边a,b,c相对应,且满足csinA=acosC.

(1)求角C的大小;

课后作业:△ABC中,角A,B,C对应边a,b,c,且2asinA=(2a+c)sinB+(2c+b)sinC.

(1)求角A的大小;

(2)求sinB+sinC的最大值.

4 提升学生数学核心素养

《普通高中数学课程标准》指出,学生在完成高中数学课程学习后,进一步提升自身数学素养能够更好地满足个人未来发展的需要,同时也符合社会发展的需求.由此可见,在高中数学复习课堂教学内容设计的过程中,应注重学生数学素养的培养,不断激发学生的学习兴趣,将学生学习的主体性充分发挥出来,使学生在复习过程中能够更好地感受、体会数学的魅力.同时,帮助学生养成积极探索、独立思考的良好学习习惯,对知识的迁移以及应用产生有效的促进作用,最终推动学生知识技能、价值观以等多方面的发展,促进学生数学核心素养的进一步提升.

借助解三角形问题与平面几何知识之间的密切联系,可以有效设置解三角形问题与三角形中的角平分线、中线等相关知识的综合应用问题.具体设计如下.

例1 在△ABC中,点D在边BC上,AD平分∠BAC,当AB=3,AC=1,∠BAC=60°时,求AD的长.

例2 在△ABC中,点D位于BC上,且∠BAC被AD平分,S△ABD=2S△ADC.

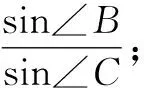
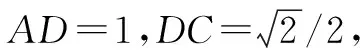
积极开展高中数学章节复习课教学活动具有重要的现实意义,需要教师深入探究教学活动的设计,为复习课教学活动的有效性提供积极保障,并于课后总结分析学生整体做题情况,及时采取相应调整措施.