求简单多面体外接球的两妙招
⦿ 陕西省西安市田家炳中学 田向红
简单多面体外接球问题是高考中的重点和难点问题,近年来在高考考查中呈上升的趋势,涉及到的题型主要是求多面体外接球的表面积、体积以及球心到指定截面的距离等问题.
1 考情分析,明析方向
通过表1对2016-2023年全国卷高考试题进行分析,发现关于棱锥(台)的外接球问题基本上每年都会出现,题型集中在选择题、填空题.试题有一定的综合性,高考命题的角度主要有:求三棱锥(台)外接球的体积、表面积以及球心到某个截面的距离等问题.解决此类问题的实质是通过化归与转化思想,最终转化为求外接球半径R.这类题能有效培养学生的空间想象能力、逻辑推理能力和数学思维品质,更好地加强学生直观想象、数学建模、数学运算等数学核心素养的落实.
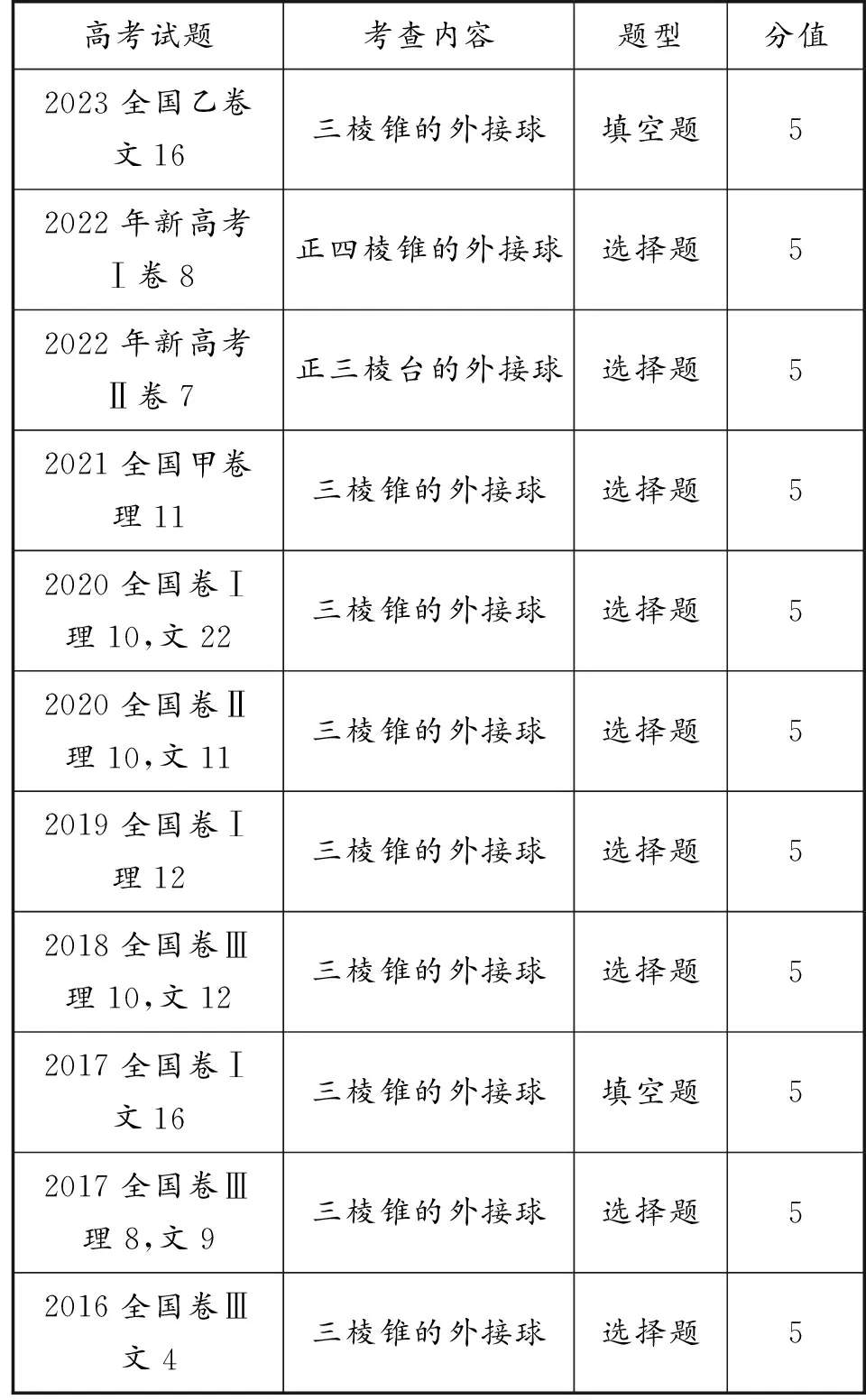
表1 考情分析
2 妙招展示,解类旁通
下面给出求简单多面体外接球的两个妙招.
妙招一:找支架
所谓找支架,就是把所给几何体补形为一些比较容易求出外接球半径的几何体.该方法也叫补形法,适用的几何体主要有正方体、正四面体、长方体、墙角型三棱锥(三条侧棱两两互相垂直).求解此类题的要点是,正方体和长方体的体对角线为其外接球的直径.
引例已知长、宽、高分别为3,4,5的长方体ABCD-A1B1C1D1的顶点都在同一球面上,求该球的表面积.
解析:如图1,设该长方体的体对角线长为l,外接球的半径为R,则l=2R,则l2=32+42+52=50=4R2.
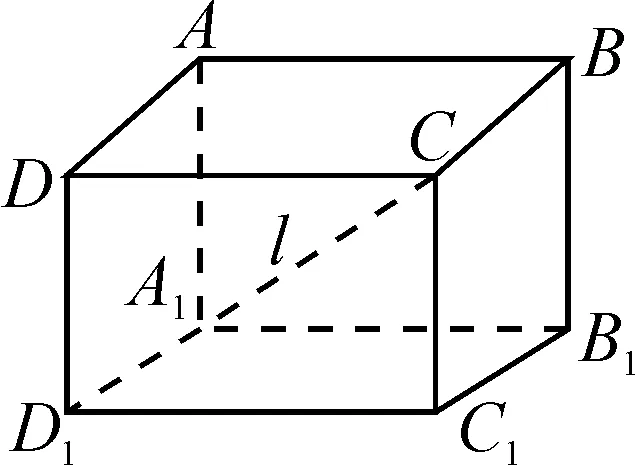
图1
故球的表面积S球=4πR2=50π.
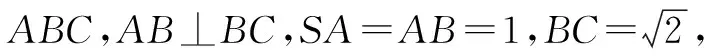
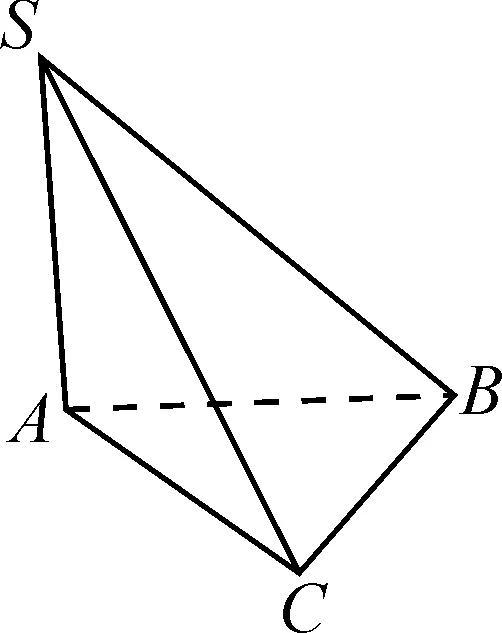
图2
点评:该题既考查了多面体外接球半径的求法,又很好地渗透了数学文化知识,可谓一举两得.
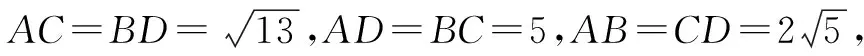
解析:由于给出的三棱锥满足对棱相等,因此可将该三棱锥补形成为长方体,则只需要计算长方体的体对角线长即可.
如图3所示,设该长方体的长、宽、高依次为a,b,c,其外接球的半径为R,则
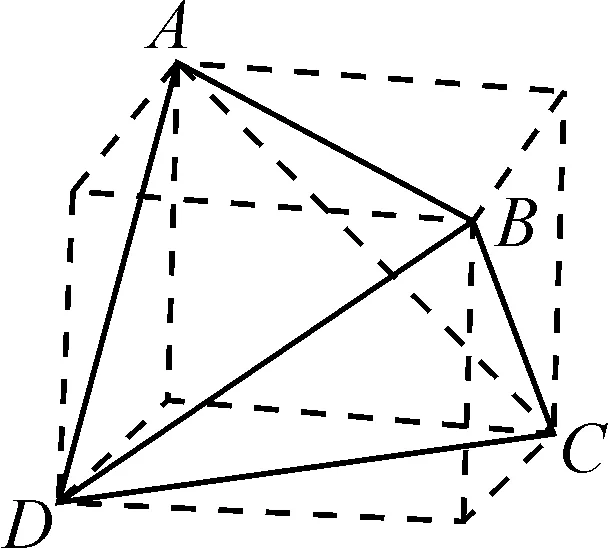
图3
整理,得a2+b2+c2=29.
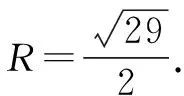
点评:这道题如果放到新课中学习,相信会难倒一大片学生,但放到高三复习备考,学生有了一定的知识积淀,很多学生会联想到补形法,问题便可迎刃而解.
妙招二:交轨法
交轨法:简单多面体外接球的球心是过各截面外接圆圆心,并且与各截面垂直的直线的交点.使用交轨法,先定截面圆圆心,再定球心,利用球的半径、截面圆的半径及球心到截面圆圆心的距离,构造直角三角形求解.
特别要注意的是:
(1)对于直棱柱或侧棱垂直于底面的锥体,找出底面多边形外接圆的圆心O1,其球心O在过点O1垂直于底面的直线上,且OO1的长度为侧棱长的一半.
(2)若棱锥的顶点构成共斜边的直角三角形,则斜边的中点就是球心.
例3直三棱柱ABC-A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°,求此球的表面积.
解析:如图4,设△A1B1C1的外接圆半径为r,圆心O1直三棱柱ABC-A1B1C1的外接球半径为R,球心为O.
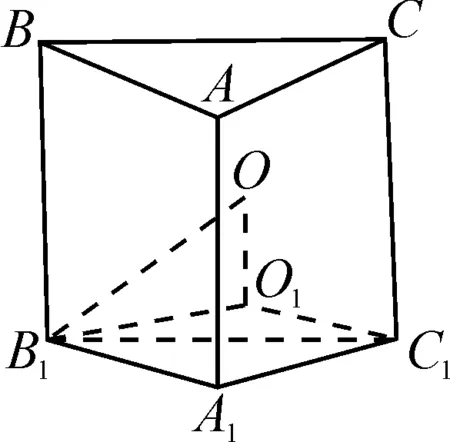
图4
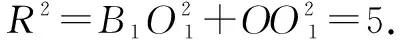
故外接球的表面积S球=4πR2=20π.
点评:此题用交轨法确定球心,思路流畅,运算简洁,很好地渗透了直观想象、数学运算等核心素养.
例4(2023年全国乙卷文16)已知点S,A,B,C均在半径为2的球面上,△ABC是边长为3的等边三角形,SA⊥平面ABC,则SA=______.

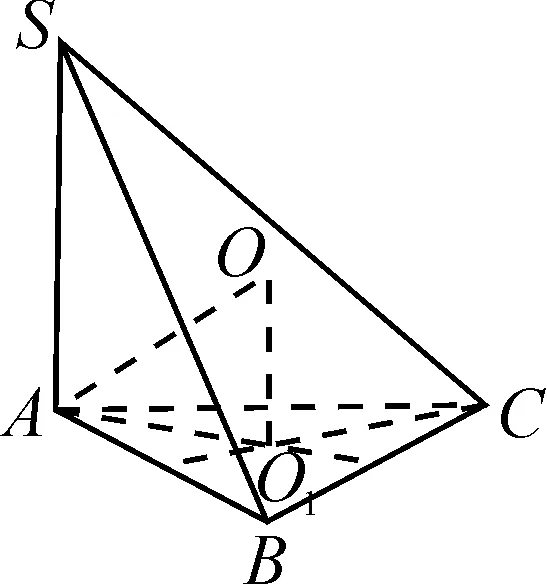
图5
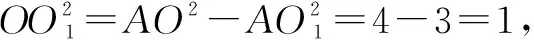
点评:解决此题的核心是明确OO1⊥圆O1,因为球心是过各截面外接圆圆心,并且与各截面垂直的直线的交点[1].
3 变式拓展,融会贯通
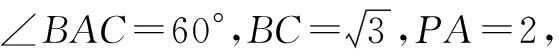
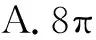
4 总结提升,精准备考
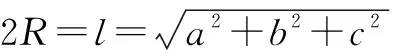
对于截面是一般三角形的问题,先利用正弦定理
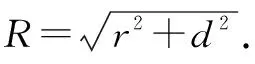
对于简单多面体的外接球问题,只要掌握上述两个妙招,有关外接球的问题便可迎刃而解.

