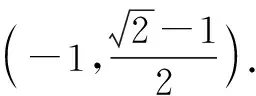合理构建函数,巧解数学问题
⦿ 江苏省海安高级中学 张 梅
在教师教学与学生学习过程中,合理构建函数,可以更好地了解与认识、处理与解决相关问题,是数学学习与数学解题中比较常用的一种基本技巧与方法.而函数作为高中数学的一条主线,是对现实问题的一种具体数学抽象,利用函数模型加以合理处理,特别在一些代数式、方程、不等式、解三角形等其他知识中,或合理改进,或无中生有,构造相应的函数模型,用函数的语言(包括概念、图象与基本性质等)来表达相关的数学问题,从而使得问题得以巧妙解决.
1 破解代数式问题
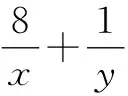
分析:将条件关系式看作关于x的方程,利用求根公式用含y的关系式来表示x,再代入所求的代数关系式,通过构造函数f(y),利用导数法确定所求代数关系式的最小值.
解析:由x+4y=x2y3,整理可得
y3x2-x-4y=0.
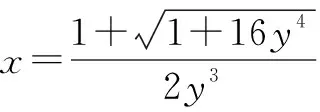


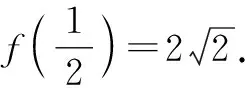
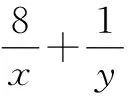
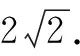
点评:借助合理数学建模,利用方程的巧妙转化与相关根的求解,结合代数式的变形,自然联想到通过构建相应的函数解决问题.导数法是破解一些代数关系式最值问题常用的技巧方法,关键是通过合理变形,将代数关系式转化为只含一个参数的函数关系式.
2 破解方程问题
例2(2023届广东省深圳市六校高三第一次联考数学试卷·8)已知x1是lnx+x=5的根,x2是ln (4-x)-x=1的根,则( ).
A.x1+x2=4 B.x1+x2∈(5,6)
C.x1+x2∈(4,5) D.x1+x2=5
分析:结合对应方程的根,通过“元”的认识,进行整体化思维,合理转化方程,巧妙同构函数.利用导数法确定函数的单调性,结合两函数值的相等关系,进而建立函数值所对应的自变量之间的关系,最后得以确定两方程的根的和式的值.
解析:由ln (4-x)-x=1,可得
ln (4-x)+4-x=5.
根据题意,可得lnx1+x1-5=0,ln (4-x2)+4-x2-5=0.
构造函数f(x)=lnx+x-5,x>0,则有f(x1)=0,f(4-x2)=0,从而f(x1)=f(4-x2).
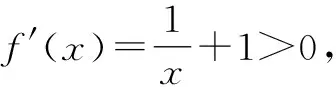
所以有x1=4-x2,即x1+x2=4.
故选择答案:A.
点评:借助整体化思维以及方程的转化与对应函数的同构,利用导数及其应用来分析并确定函数的单调性,利用两函数值相等的条件进行性质的应用,从而得以方程化处理问题.借助方程的转化与函数的同构,通过函数单调性的确定,从“数”的视角来合理构建,巧妙破解.
3 破解不等式问题
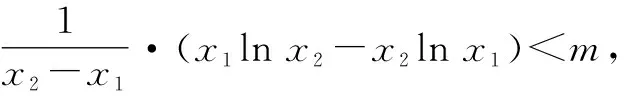
分析:不失一般性确定变量的大小关系,进而根据原不等式进行恒等变形与转化,合理构建函数,结合函数值的大小关系来确定该函数的单调性,通过求导处理,结合导函数所对应的不等式恒成立来转化,结合不等式的性质以及对应函数的单调性来确定参数的取值范围问题.
解析:不妨设1≤x1

即x1(lnx2+m) 因为函数y=1-lnx在区间[1,e]上单调递减,所以1-lnx的最大值为1-ln 1=1. 所以m≥1. 故填答案:[1,+∞). 点评:借助不等式的巧妙转化与变形,通过合理构建,结合同构函数法进行处理是破解此类问题中比较常见的技巧方法.破解的关键就是合理恒等变形与转化对应的不等式或函数式,进而合理构建,利用函数的基本性质(单调性)来合理转化,进而得以巧妙求解. 分析:由已知结合余弦定理建立不等式b2>a2+c2,又结合三角形的性质知a+c>b,放缩处理建立对应的不等式,通过换元处理构建单变量函数,从不等号两边分别利用构建函数并结合求导处理,通过函数的单调性与极值来确定对应的取值范围,进而得以确定其对应的取值范围问题. 解析:由题意可知cosB<0,结合余弦定理,有 b2=a2+c2-2accosB>a2+c2. 又由三角形的性质,知a+c>b,则当c≥a时, 点评:涉及解三角形最值问题的常见技巧策略是利用不等式和消元构建函数求解,多元变量可以逐个消元,也可以利用齐次消元,还可以利用某些不等关系消元.构建函数,利用求导处理,是破解此类问题是比较有效的基本手段与方法之一. 构建函数既是一种方法,更是一种意识.合理根据数学思维方式,结合函数的概念、图象与基本性质等,建立起与相关问题相吻合的函数模型,合理改进,巧妙创新.在数学解题过程中不断学习、深入、适应、模仿、套用、改进并创新,从而更加深入地借助函数来解决一些相关问题,不断加深对相应数学概念的掌握、数学知识的理解以及数学模型的应用,举一反三,融会贯通,进而提高数学能力,培养数学核心素养.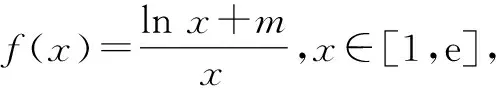

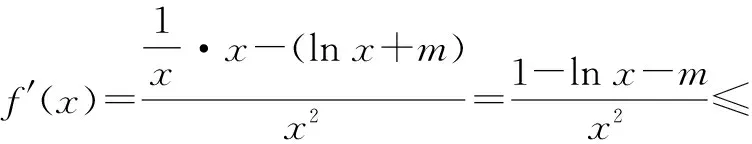
4 破解其他问题