例谈建构思维的培养措施

⦿ 江苏省宿迁中学 孙彩红

学习不仅是知识的学习,更重要的是学习方法的获得.这就要求学生摈弃死记硬背的学习方式,在现有的学习条件下实现自我发现与知识的构建.因此,真正有意义的学习是在以学生为中心的基础上,鼓励学生主动发现、探索与建构新知的过程.建构主义作为认知心理学派中的一个分支,是当前教育改革的理论基础之一.它对培养学生的学习能力与创新能力具有重要作用.

从建构主义观的层面来看,学习的目的不仅在于理解知识,更在于对新知的观察、分析、检验与批判等[1].学生建构新知需经历同化与顺应两个阶段.因此,我们可将学生原有的认知结构作为新知形成的起点,让学生将新知内化到原有认知中,协同建构出新的认知结构.

高中数学建构教学是以建构主义理论为基础,将教学内容、方法、过程等看成一个整体,以建构思维的培养与运用为核心,践行知识与能力互相转化的过程[2].为了有效培养学生的建构思维,促进学生综合能力的发展,笔者以不等式问题的探究为例,谈一些自己的看法.

1 模式积累,促进外源建构思维的形成

所谓外源建构是指学生通过具有一定意义的学习后,建构标准的知识与技能,其结果符合双基的外在评判标准.评判学生有没有从真正意义上掌握知识与技能,可从以下两个标准来衡量:①能否将新知纳入原有的认知结构中,与原有的认知体系建立联系,让知识变得系统、整体化;②能否将新知进行具体化,且灵活地运用于生活实践.

在不等式的教学中,模式识别是最重要的解题思想.学习中,学生获得的经验、知识等经过认知结构的加工,会形成新的结构与类型,便于大脑长久保存,这种模式与类型我们统称为模式.学习中,学生会因教学内容与方法的区别建构各种不同类型的模式,并将这些模式以简单编码的形式存储在记忆中.

解题时,学生输入问题,则会初步联想之前解决过的类似问题,辨认该问题属于哪类模式,在这种索引的引导下,从原有的记忆中提取适合解决此问题的模式,实现解题.因此,模式积累尤为重要.学生在解题训练中通过问题特征的识别,将模式不断地建构到大脑中,完成内化与积累的过程.利用不等式的模式积累,促进外源建构思维的形成是高中数学教学中促进学生建构思维生长的常用方法.

(1)基本不等式链

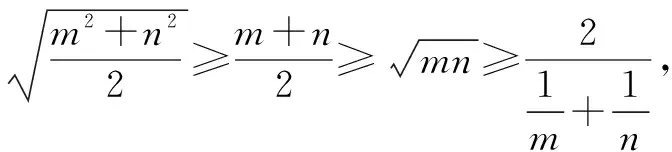
(2)用基本不等式求最值

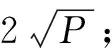
遇到利用均值不等式求最值的问题时,有三点需要注意:①函数式中的每一项都是正数;②函数式中含有变量的项的和或积是定值;③等号成立的条件不可缺失.

(3)三元或n元基本不等式

n个正数a1,a2,a3,……,an的算术平均数不小于a1,a2,a3,……,an的几何平均数,即

当且仅当a1=a2=……=an时,等号成立.

除以上几种模式以外,还有绝对值不等式、二维形式的Cauchy不等式等模式.这些模式体现了思维定势对学习正迁移的积极作用.学生将这些模式纳入自己的认知结构中,在遇到问题时能快速找出大脑中储存的模式,缩短解题时间,保证正确率.

做好模式识别与积累,需注意下列几点:①将模式的类型与范例,打包成一个整体进行记忆;②基本模式可直接作为解题依据,解题时不需要再次回归到原始推理过程中去;③要突破思维定势,善于变通.模式只能说是相对稳定的,但特殊问题需特殊对待,遇到非常规性的问题时,应创新出更高阶的模式.

2 模式直观,促进辩证建构思维的形成

辩证建构思维是指通过一系列教学活动的开展,学生对已有命题的再发现,其核心是学生的再发现和原有的命题或概念呈辩证统一的关系.教学中,常以一题多解等方式对学生进行思维训练,帮助学生实现再发现,且让这种再发现贯穿于整个教学过程中.

不等式的证明缺乏直观事物作为解题的支撑,模式直观则能弥补这个缺失.模式直观就是将一些抽象的,缺乏图形支撑的代数问题转化成学生所熟悉的,且被大众所接受的思维模式,以此为背景进行创新.

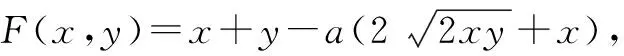
此题可从以下两种直观模式角度来理解.

(1)分离参量

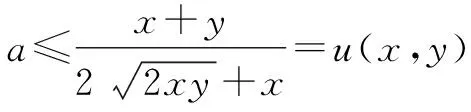
(2)基本不等式

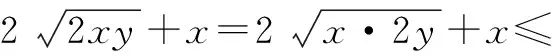
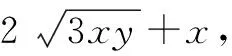
为此,笔者带领学生进行了模式的创新,分别从“待定系数”和“集中变量”的角度去思考与分析问题.学生在待定系数的模式中亲历矛盾的普遍性和特殊性,并根据其内在的联系获得“再发现”,辩证建构思维在认知冲突中逐渐形成.

数学本就具有对称美、相似美、奇异美等,而这些美感因素是学生获得直觉思维的源泉,学生在对数学美的挖掘与审视中促进思维的“再发现”.因此,在解题中追求简洁、直观是实现解题能力提升的基本保障.

3 模式质疑,促进内源建构思维的形成

内源建构思维主要是指学生在实验、分析或推理(合情或逻辑)中,实现概念或命题的再发现.每个学生都有独特的个性特征,在对知识的概括、总结与提炼中,其思维活动与形成的数学思想方法均存在着一定的差异性.为此,新课标一再强调要张扬学生的个性,让学生在有意义的学习中,获得扎实的数学能力.而外源建构思维与辨证建构思维又有着千丝万缕的内部联系.因此,学生个性的发展与能力的提升需内源建构思维的支撑.

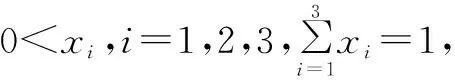
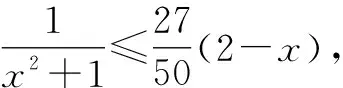
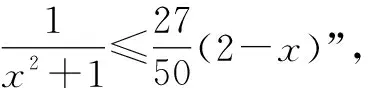
学源于思,而思又来自于疑.质疑是推动思维进步的基本条件,也是学习者产生探索欲的标志.学生在认知冲突中,不断提出质疑,解决质疑,从而获得新的结论.鉴于此,教学中,教师应不断设置能引起学生认知冲突的悬念,以激活学生的探索欲,让学生在质疑与探究中充分发挥自己的个性特性,形成良好的个性认识[3].

建构思维的培养能将学生引入更为宽阔的领域,体验学习带来的乐趣,达到优化并整合学生原有认知结构的效果.而模式的积累、直观与创新对建构思维的形成与发展具有举足轻重的作用.因此,教师应在教学的每一个环节有意识地培养学生的建构思维,鼓励学生勤积累、敢质疑、勇创新,使得建构思维成为激励学生主动探索与发现的动力.