利用构造法解决极值点偏移问题
——以2022年高考全国甲卷理科数学第21题为例
刘 灏
(华南师范大学数学科学学院,广东 广州 510631)

1 数学问题分析
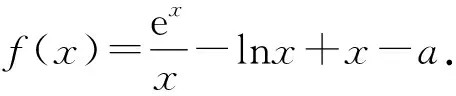
(1)若f(x)≥0,求a的取值范围.
(2)证明:若f(x)有两个零点x1,x2,则x1x2<1.
分析函数定义域(0,+∞),第(2)问中暗含f(x1)=f(x2)=0.通过第(1)问的计算得到极值点恒为x=1,那么第(2)问即等价于“求证x1x2 所以当x∈(0,1)时,f′(x)<0;当x∈(1,+∞)时,f′(x)>0,所以f(x)在(0,1)上单调递减,在[1,+∞)上单调递增. 所以f(x)min=f(1)=e+1-a. 若f(x)≥0,则e+1-a≥0,解得a≤e+1. 所以a的取值范围为(-∞,e+1] 设h(t)=et+t-a,则h′(t)=et+1>0. 所以h(t)min=h(1)=e+1-a. 若f(x)≥0,则e+1-a≥0, 解得a≤e+1. 所以a的取值范围为(-∞,e+1]. 又f(x1)=f(x2), 此处我们对不等式进行拆分, 所以p1(x)在(1,+∞)单调递增. 所以当x∈(1,+∞)时,p1(x)>p1(1)=0. 综上,当x∈(1,+∞)时,p1(x)>0,p2(x)<0,所以p1(x)-2p2(x)>0. 第一种方法是直接法,将f(x)≥0在定义域(0,+∞)上恒成立的问题直接转化为f(x)min≥0,运用导数求出函数f(x)的单调区间,进而求出函数的最小值,最后求出参数范围. 第二种方法是运用整体思维,即指数、对数函数的代换,使函数f(x)通过换元处理为复合函数f(g(x)),利用复合函数的单调性求f(x)的最小值,适当地减轻了计算量. 极值点偏移问题是近年高考压轴题的常客,同时新高考比之前全国卷试题更复杂,情境更综合,这可能也是许多学生在新高考下不能顺利得分的一个原因,但这也是新高考的一种趋势.正如新课标指出“基于数学核心素养的教学评价,不仅要关注学生对知识技能的掌握程度,还要更多地关注学生的思维过程[2].” 此类题型涉及化归、换元、分类讨论等数学思想、同时考查导数和不等式的基础知识,难度逐级递增环环相扣. 希望学生能熟练掌握极值点偏移问题中的构造函数法,学习其数学思想,领略数学魅力,也希望各位数学教育工作者能提出更多更精妙的极值点偏移问题,教学相长,共同进步!1.1 第(1)问解析
1.2 第(2)问解析

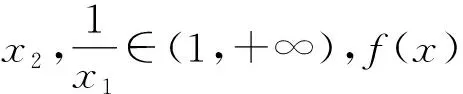






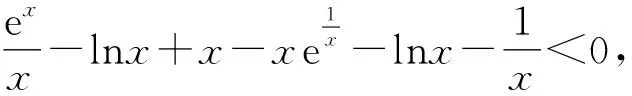




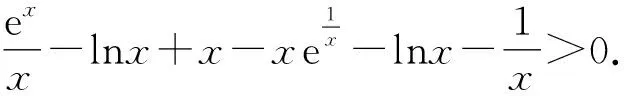

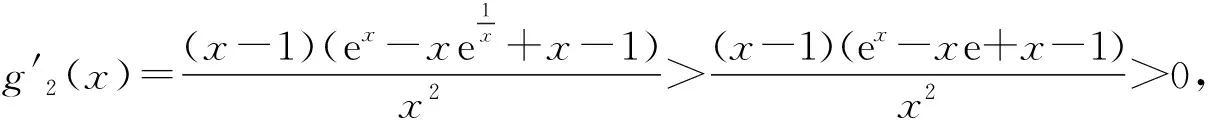
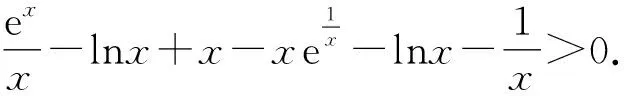




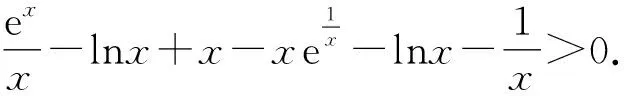

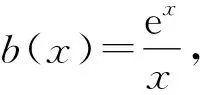
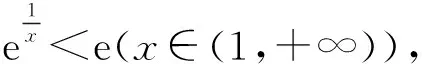

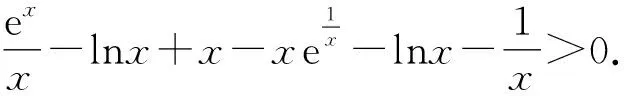
2 解题方法讨论
2.1 第(1)问的解题思路
2.2 第(2)问的解题思路
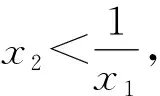
3 总结与展望

