一类数列型不等式问题的证法探究

甘肃省庆阳市镇原县屯字中学 (744502) 郭宏刚

以基础函数“lnx”作为题设背景的数列型不等式证明一类问题,是出现在近年高考或各地模拟考试中的热点题型,这类问题常与导数应用紧密联系,把与lnn(n∈N*)相关联的数列型不等式的证明设置在试题的最后一问,证题时利用前面小问中的导数研究函数单调性结论来证明.下面以一道高三阶段性测试题来探究一类数列型不等式的证明方法.

1 试题呈现

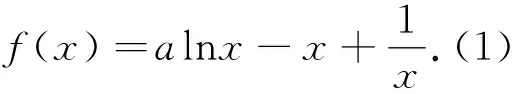
该题以基本函数“lnx”为题设背景,其中第(2)小题是证明数列型不等式问题,这一小题解答的基本路径是:逆向分析,寻找与所证不等式等价的不等式,通过构造函数,运用导数知识推得基础函数的不等式,进而将结论予以赋值转化为数列的不等关系,最后利用数列比如裂项、累加等方法,或运用“放缩法”证得数列不等式.

2 试题解答

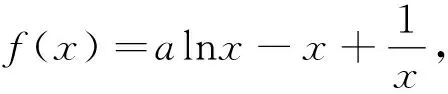
①当a≤0时,易知当时当x>0时,f′(x)<0,此时f在(0,+∞)上单调递减.

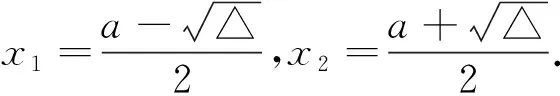
当x变化时,f′(x),f(x)变化情况列表如下:

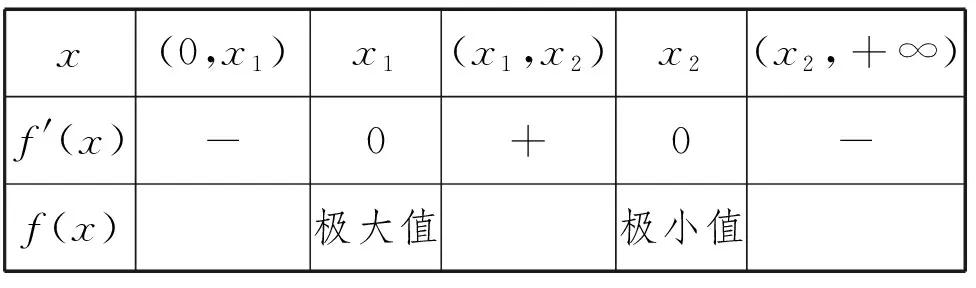
x(0,x1)x1(x1,x2)x2(x2,+∞)f'(x)-0+0-f(x)极大值极小值

综上所述,当a≤2时,f(x)在(0,+∞)上单调递减;当a>2时,f(x)在(0,x1),(x2,+∞)上单调递减,在(x1,x2)上单调递增.

下面重点探究第(2)问中数列型不等式的证明.

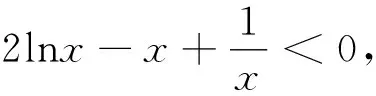
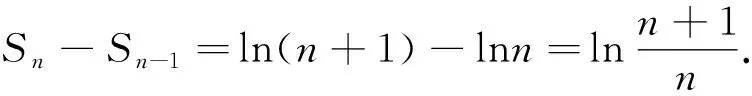
点评：证法1首先将所证的数列不等式进行逆向分析,结合其结构形式的特点,利用由(1)函数单调性所证得的不等式证明.

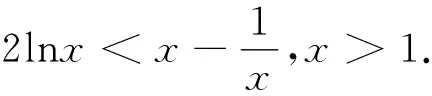
点评：证法2在由(1)函数单调性所证得的不等式的基础上,通过赋值、累加证得所证不等式.

为了介绍证法3,这里给出对数均值不等式.

对数均值不等式证明详见文[1].

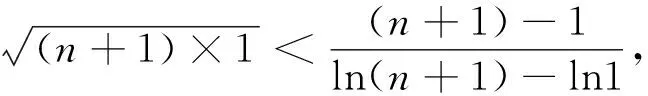
3 变式探究

若稍加改变一下题设中的函数表达式,第(2)小题中所证的数列型不等式不变,则有:

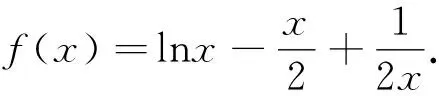
(1)解关于x的不等式f(x)>0;

解析：(1)易得f(x)>0的解集为(0,1).

(2)同上述测试题的证法.若将题设条件中的函数式改为关于基础函数“ex”的不等式,所证的数列型不等式不变,则有:

变式2 (2022年新高考Ⅱ卷的第22题)已知函数f(x)=xeax-ex.

(1)当a=1时,讨论f(x)的单调性;

(2)当x>0时,f(x)<-1,求a的取值范围;

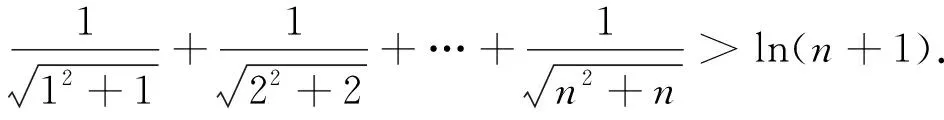
由此可以看出,上述测试题的第(2)小题其实就是该高考题的第(3)小题.在强调高考命题深化改革的今天,通过改编、整合等手段来给予以往高考真题新的生命,从而演变为新的试题,已成为高考命题的一种常态化趋势.以“题”为鉴,这就启示我们在复习备考的过程中重视对以往高考真题的深层次探究,通过探究,分析高考命题和考查的思想方法、本质及学科核心内容,关注命题者的意图、解题需要的能力和科学的思维方法,使复习跳出题海,并“打磨利器,有的放矢”,利用对以往高考真题检验复习效果,使复习备考“择高处立,向阔处行”.

解析：(1)f(x)在(0,+∞)上单调递增.

(2)a=1.

4 方法总结

对比上面三种证法,利用对数均值不等式(即证法3)证明数列型不等式,可以避开求导、应用导数研究函数单调性等复杂过程,简捷明了、操作性强,是证明数列型不等式这一类问题的通性通法.

运用对数均值不等式证明与lnn(n∈N*)相关联的数列型不等式的方法步骤是:分析→选取→赋值→得证,即:①分析研究所证数列不等式的结构特点;②合理选取对数均值不等式链中的某个不等式;③对选取的对数均值不等式链中的不等式中的a,b恰当赋值,有时结合放缩技巧;④证得不等式.

对典型试题解法的探究,就是指对问题从不同视角来审视,以不同的切入点探究问题,其实质是对试题的“二次开发”.通过对试题的剖析和思考,展开问题的来龙去脉和知识间的纵横联系,站在一定的高度去思考问题,突出数学本质,使知识达到融会贯通,使思维得到升华,进而优化数学思维品质.