从竞赛视角探究一道征解题

重庆市两江中学校 (401120) 彭 锋 邓元洁

《数学通讯》(上半月刊)2022年第10期问题征解第573题隐含了一个经典的竞赛不等式,本文从竞赛的视角对这道征解题的变式作了深入地探究,最后给出了三个推广.

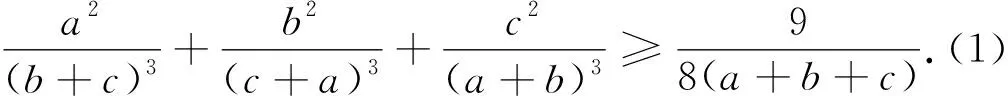
这是一个分式不等式,左边各项的分子与分母分别是2次、3次单项式,只要稍加变形,就会利用柯西不等式获证.

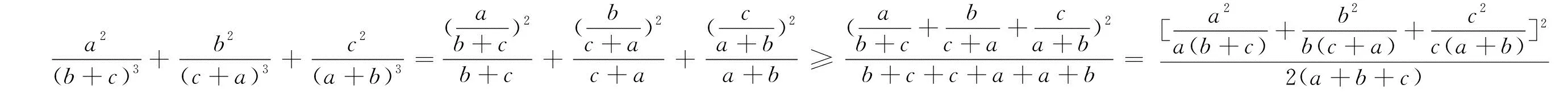
如果把不等式(1)右边分母中的(a+b+c)分别放到左边各项的分子,展开后与分母进行重组,那么利用权方和不等式即可获证.

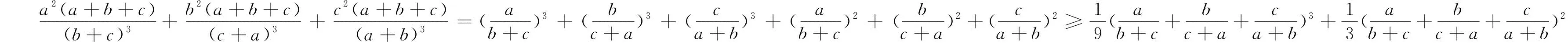
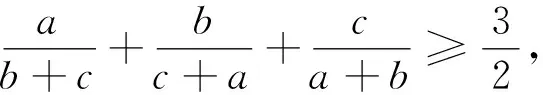
不等式(1)隐含了一个经典的竞赛不等式,由此引发笔者联想到历届有关的竞赛不等式,从而对不等式(1)的变式加以探究,得到下面的问题.

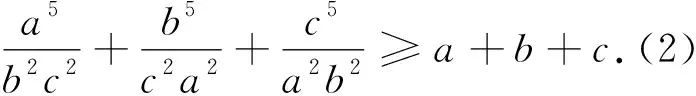
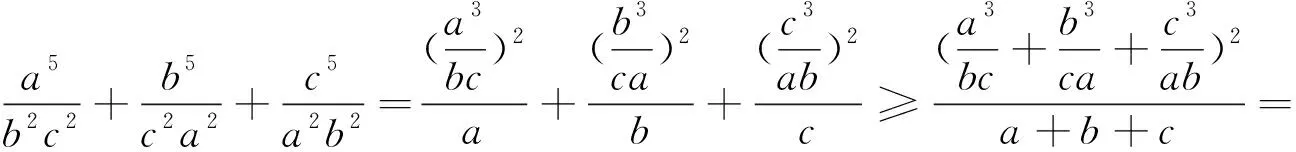
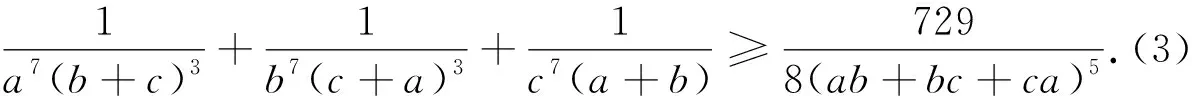
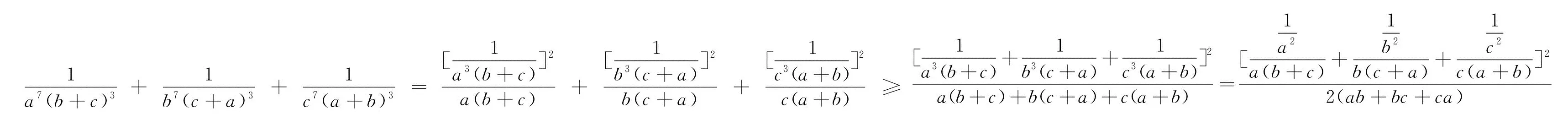
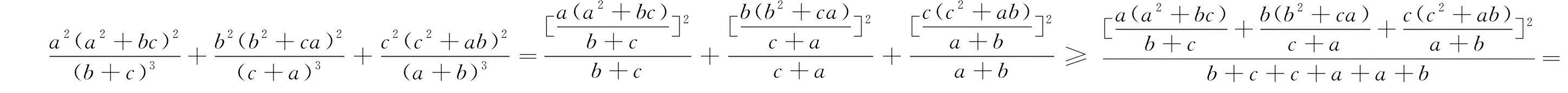
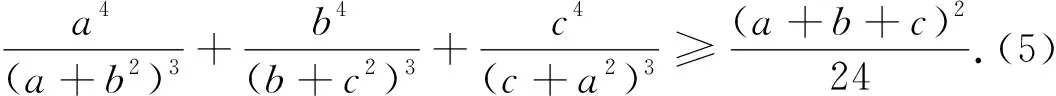
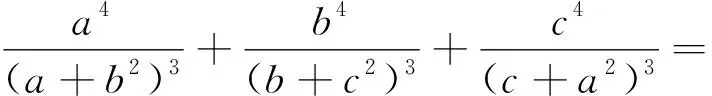
点评：如果直接用权方和不等式,得到

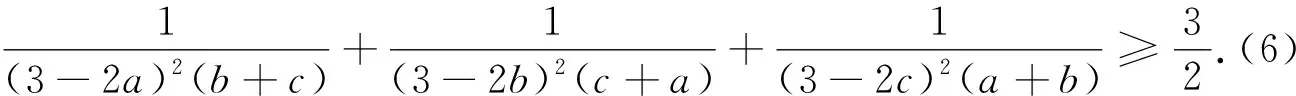
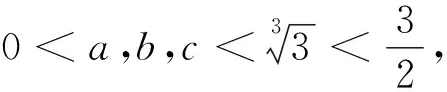
即不等式(6)成立.

点评：从问题2到问题6,分别隐含了2002年加拿大数学奥林匹克不等式竞赛题,1995年第36届国际数学奥林匹克不等式竞赛题,2018年全国高中数学联赛陕西赛区预赛不等式竞赛题,2011年克罗地亚数学奥林匹克不等式竞赛题,2022年塞尔维亚数学奥林匹克不等式竞赛题,由此从某种意义上进一步揭示了这些经典的竞赛不等式之间的内在联想.

把问题1推广,可以得到

推广1 已知a,b,c,m是正数,求证:

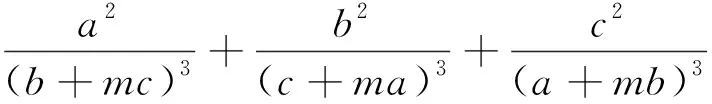
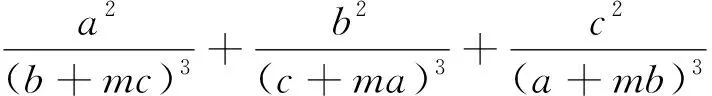
推广2 已知a,b,c,n是正数,求证:

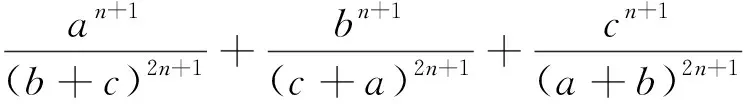
推广3 已知a,b,c,m,n是正数,求证:

同推广2可证.