例析SOS-Schur方法在不等式中的应用

上海华育民办中学 (200135) 卢 亮

把一个关于a、b、c的三元不等式化为M(a-b)2+N(c-a)(c-b)≥0的形式,并设法证明其成立的方法我们称为SOS-Schur方法,这个方法是SOS(平方和)方法的变通,平方和方法可以参见文[1],SOS-Schur方法可以解决一些SOS方法难以解决的问题,本文通过一些例子阐述SOS-Schur方法的运用.

首先给出三个本文例题解答所需的可化为M(a-b)2+N(c-a)(c-b)形式的代数式.

结论1a2+b2+c2-ab-bc-ca=(a-b)2+(c-a)(c-b).

易证,过程略.

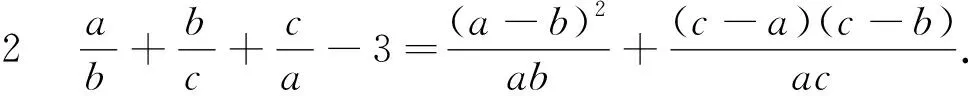
利用结论2的证明方法或直接利用结论2的结果可以证明,过程略.

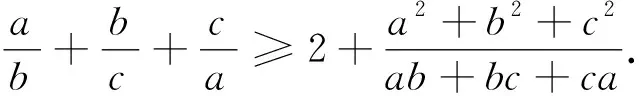
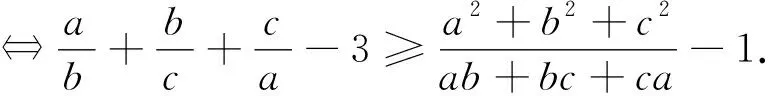
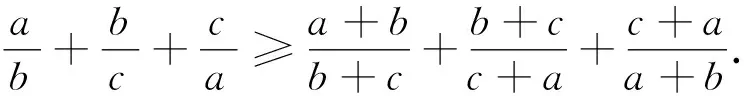
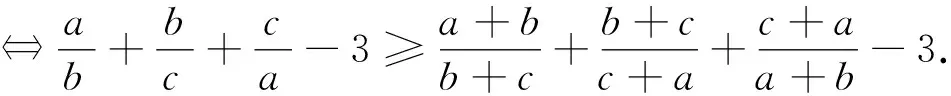
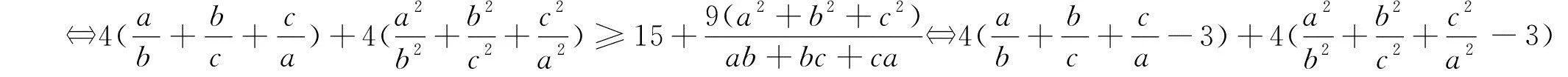
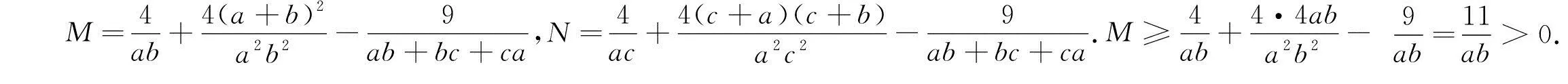
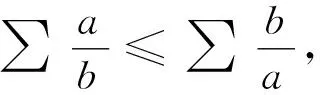
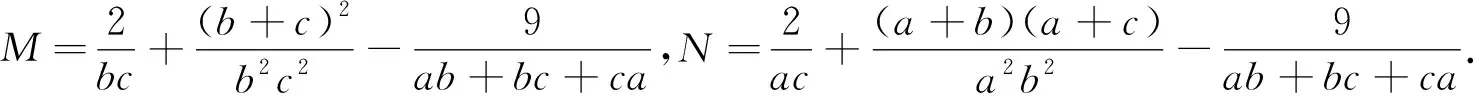
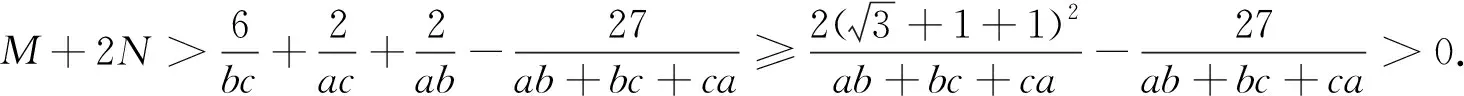
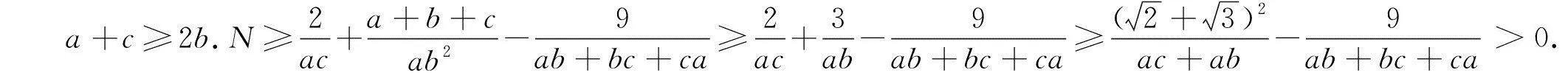
综上,原不等式成立.

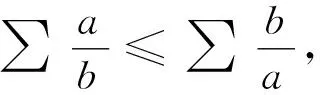
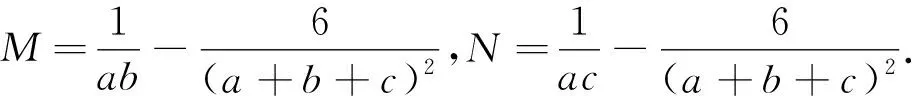
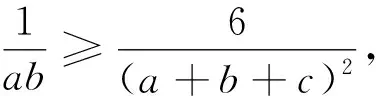
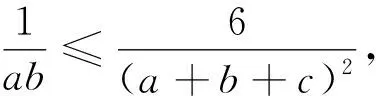
综上,原不等式成立.

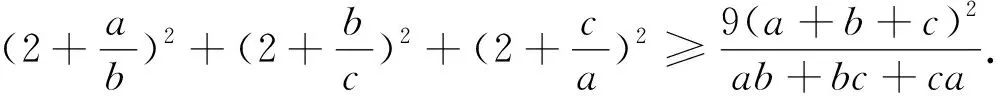
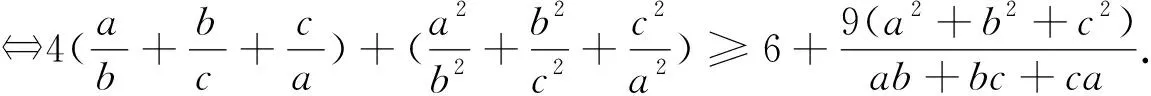
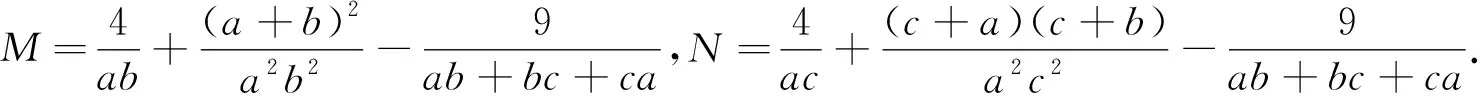
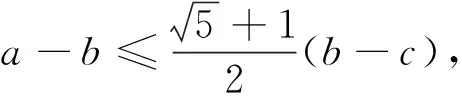
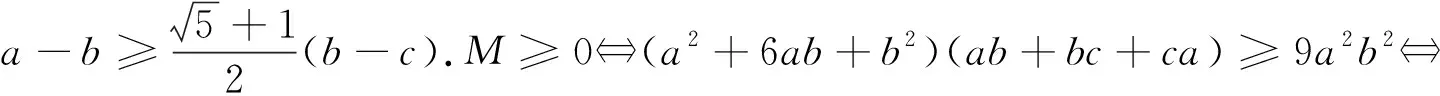
综上,原不等式成立.