例谈放缩法在求解导数问题中的妙用*

北京市第八十中学 (100102) 李 丁

放缩函数与放缩参量在取值范围、不等式恒成立等问题中经常使用,其重要性不必赘述.很多导数题目可以转化为上述问题,学生在使用上述方法时,往往会出现一种倾向,即看到题目就想构造函数然后求函数的最值,以至于导致后续函数式过于复杂,而不能求解.事实上,我们要认识到每一种方法的运用都不能教条主义,本文通过几个典型例题的分析求解,旨在帮助学生们辩证处理此类题目,多一种考虑问题的角度,进而做到择其优者而选之.

解：(1)解法同高考参考答案,不再赘述.

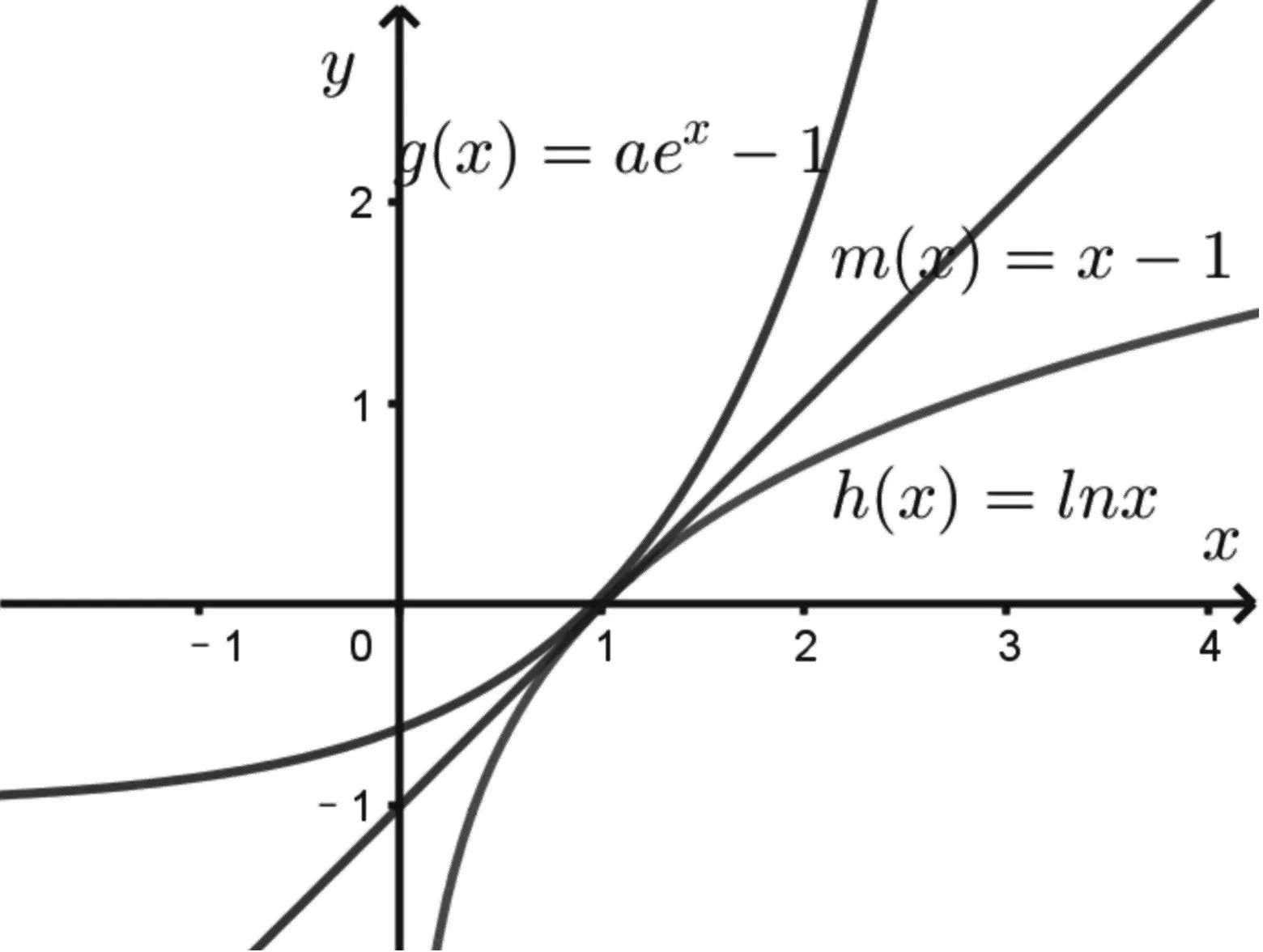
图1

解法：(1)解法同高考参考答案,不再赘述.

(2)法一:(放缩函数法)f(x)+e≥0即ax2+x≥-ex+1+1.令m(x)=ax2+x,g(x)=-ex+1+1,如图2,做g(x)在(-1,0)处的切线h(x)=-x-1.

欲证f(x)+e≥0,只需证m(x)≥h(x)≥g(x),下面证明h(x)≥g(x).令F(x)=h(x)-g(x),即F(x)=ex+1-x-2,即证明F(x)≥0.F′(x)=ex+1-1,F′(x)=0,x=-1,当x∈(-∞,-1)时,F′(x)<0,则F(x)在(-∞,-1)单调递减,当x∈(-1,+∞)时,F′(x)>0,则F(x)在(-1,+∞)单调递增,F(x)min=

F(-1)=0,所以F(x)≥0,即h(x)≥g(x).下面再证明m(x)≥h(x),即证明m(x)-h(x)≥0,令H(x)=m(x)-h(x)=ax2+2x+1,由于a≥1,Δ=4-4a≤0,所以H(x)=m(x)-h(x)≥0,即m(x)≥h(x).由以上可知m(x)≥h(x)≥g(x),即f(x)+e≥0.

(2)若1

解：(1)易解,不再赘述.

(2)法一:(放缩函数法)f(x)<-1即lnx

图3

下证m(x)>h(x).令H(x)=m(x)-h(x)=ax2-2x+1,由于10,即m(x)>h(x).

总结：放缩函数法运用以直代曲思想,做出切线,把曲线根据需要放缩为直线,利用切线与曲线的位置关系加以证明.放缩参量法运用放缩参量的方法成功避免了求含有参数函数的最值,使不等式证明变得简单化.