一道三角最值问题的多解及拓展

广东省佛山市罗定邦中学 (528300) 范光玉

解三角形问题的常用解题思路是利用正余弦定理,实现边角的互化后进行求解;其次三角形作为平面图形,其自身具有丰富的几何性质,我们还可通过几何的视角来进行求解.本文对2022年新课标Ⅰ卷第18题的多解进行分析并将问题拓展到一般结论.

一、题目呈现

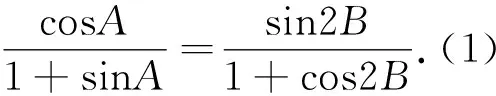
本题的主题干较为简单,考察二倍角等三角恒等变换的相关公式获得△ABC三个内角间的关系,在此基础上求解第(1)问就较为简单;本题的难点主要集中在第(2)问,所求式考察了三个变量间的关系,观察其结构发现其为齐次式,我们可以通过构造边与边之间的比例进行消元;其次,也可通过边化角后构成比例关系进行消元.

二、多解分析

对于第(2)问,主题干是关于角的关系,为此自然想到利用边化角来进行求解.

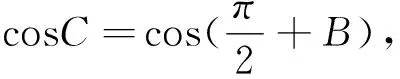
评注：上述解法将所有变量都用cosB来表示,实现了化简的目的,再利用基本不等式或利用“对勾函数”的性质即可求解.

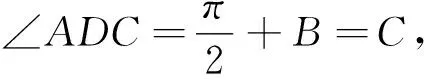
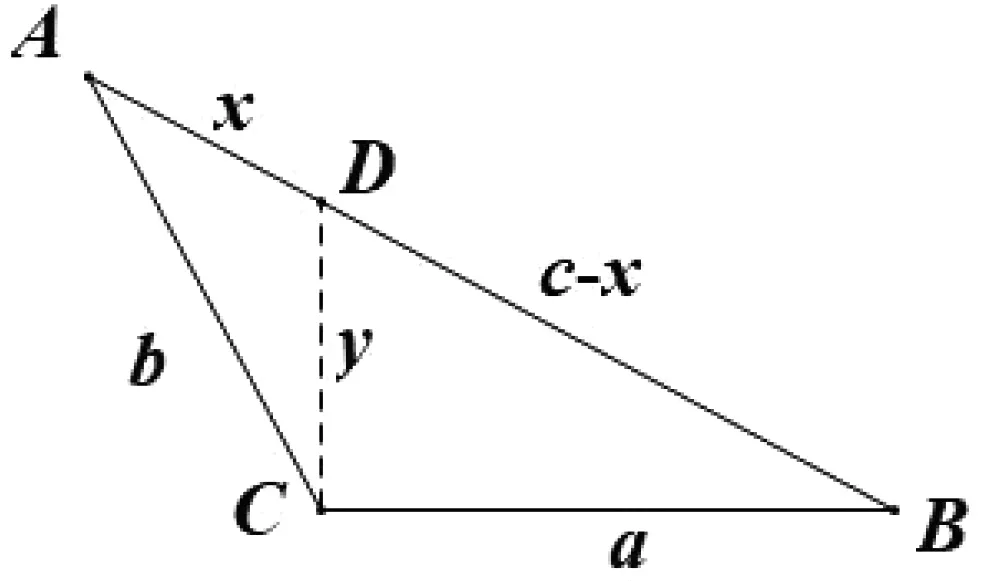
图1

评注：本题的核心是发现三角形相似,从而获得边之间的关系,再利用勾股定理实现了消元,再利用齐次化的思想求解.

解法三：(利用几何性质及边化角求解)

如图2,在图1的基础上延长BC,过点A作BC延长线的垂线,垂足为E.在解法二的基础上可知在ΔAEC中,∠EAC=B,故可得AE=bcosB,CE=bsinB.在ΔAEB中,AE=csinB,CE+a=ccosB.结合正弦定理即得sin2C=cos2B,sin2A=cos22B成立,后续解法同解法一.

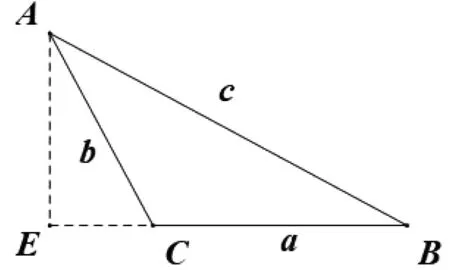
图2

三、问题拓展

通过对上述解答过程的分析,我们可将原问题进行拓展.

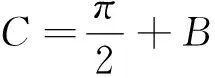
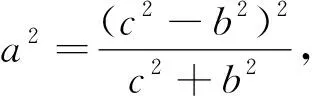
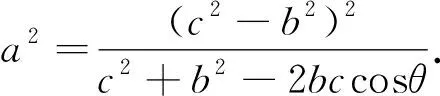
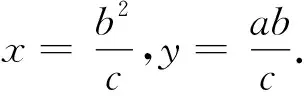
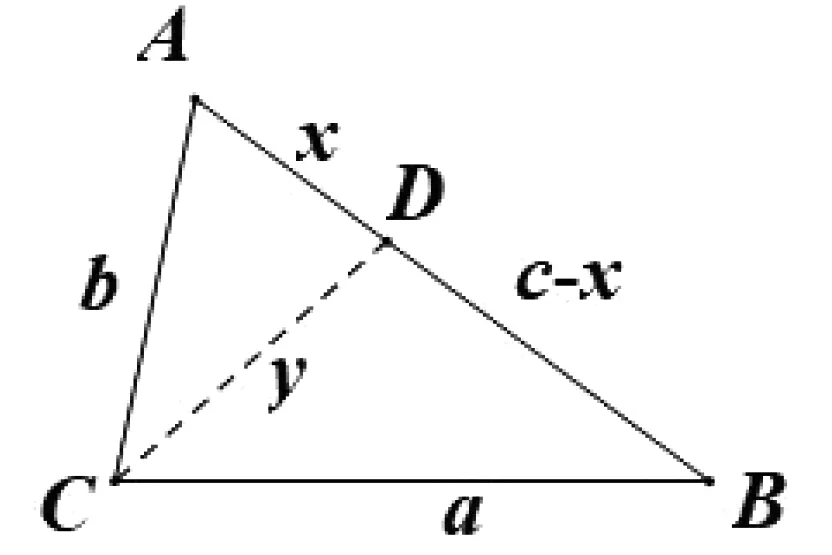
图3