利用导数研究函数的零点问题
刘 爽
(杭州蕙兰未来科技城学校)
处理有关函数的零点(也就是方程的实数根)问题时,往往需要借助导数知识加以灵活分析,充分体现了“导数”是分析、解决函数零点问题的有力工具.本文结合高考真题加以剖析,旨在说明常见考查题型及其求解思路,进而提高读者求解此类问题的能力.
1 根据函数的零点个数,求参数的取值范围
若题目给出函数的零点个数,则往往可在求导分析函数单调性的基础上,灵活采用数形结合的方法,构建含有参数的不等式(或不等式组)求解问题.
例1(2014年全国Ⅰ卷理11)已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围为( ).
A.(2,+∞) B.(1,+∞)
C.(-∞,-2) D.(-∞,-1)
解析当a=0时,f(x)=-3x2+1,显然有两个零点,故不符合题意.
当a≠0时,易知f′(x)=3x(ax-2).
若a>0,令f′(x)>0,得x<0 或x>;令f′(x)<0,得0<x<. 于是,函数f(x)在(-∞,0)和(,+∞)上单调递增.又注意到f(0)=1,f(-1)=-a-2<0,据此画出函数f(x)的大致图像,如图1所示.由图可知f(x)在(-∞,0)上有零点,这与题设条件“f(x)存在唯一的零点x0,且x0>0”矛盾.
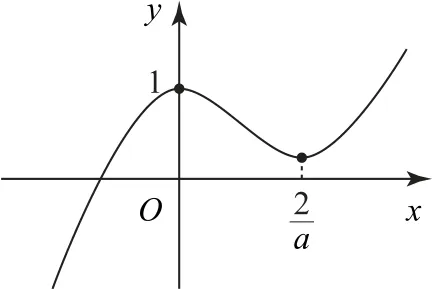
图1
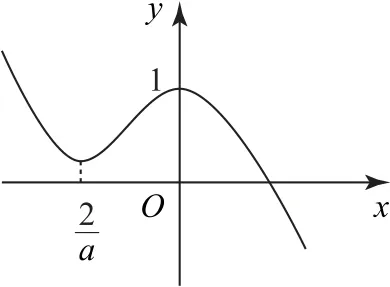
图2
综上,a的取值范围为(-∞,-2),故选C.
点评本题侧重考查“分类与整合思想”“数形结合思想”在解题中的综合运用,求解的关键是利用导数分析函数的单调性.
2 考查方程的实根个数问题
一般地,方程f(x)=0的实根个数是函数f(x)的图像与x轴的交点个数,也就是函数f(x)的零点个数,所以可灵活运用函数观点处理问题.
例2(2013 年安徽卷理10)若函数f(x)=x3+ax2+bx+c有极值点x1,x2,且f(x1)=x1,则关于x的方程3[f(x)]2+2af(x)+b=0的不同实根个数是( ).
A.3 B.4 C.5 D.6
解析易知f′(x)=3x2+2ax+b,依题意可知x1,x2是方程3x2+2ax+b=0 的两个实根.当x1<x2时,易 知x1是函数f(x)的极大值点,x2是函数f(x)的极小值点,又注意到f(x1)=x1,因此可在同一平面直角坐标系中分别画出函数f(x),直线y=x1,y=x2的图像,如图3所示.由图可知f(x)=x1有2个不同的实根,f(x)=x2有1个实根,从而共有3个不同的实根.
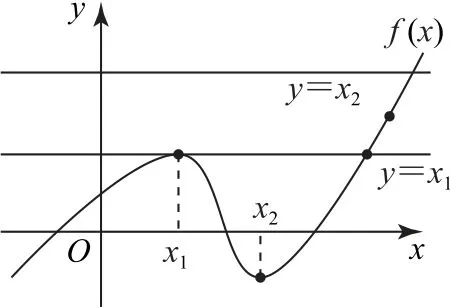
图3
当x1>x2时,易知x2是函数f(x)的极大值点,x1是函数f(x)的极小值点,又注意到f(x1)=x1,因此可在同一平面直角坐标系中画出函数f(x),直线y=x1,y=x2的图像,如图4 所示.由图可知f(x)=x1有2个不同的实根,方程f(x)=x2有1个实根,从而共有3个不同的实根.
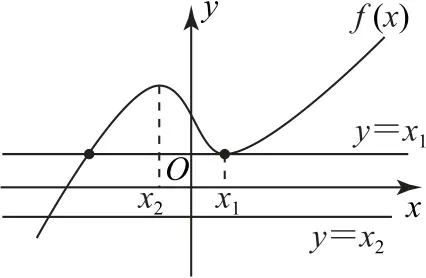
图4
综上,关于x的方程3[f(x)]2+2af(x)+b=0的不同实根个数是3,故选A.
点评本题具有一定的难度,对考生分析、解决问题的能力要求较高,求解的关键在于两点:一是实施“换元”变形、灵活转化目标问题;二是综合运用“分类与整合思想”“数形结合思想”以及“转化思想”巧解题.
3 证明函数的零点个数
一般地,若函数f(x)在[a,b]上单调递增(或单调递减),且满足f(a)f(b)<0,则函数f(x)在(a,b)上存在唯一的零点(即存在唯一的x0∈(a,b),使得f(x0)=0).
例3(2019年全国Ⅰ卷理20)已知函数f(x)=sinx-ln(x+1),f′(x)为f(x)的导数.证明:
(1)f′(x)在(-1,)上存在唯一极大值点;
(2)f(x)有且仅有2个零点.
(2)易知函数f(x)的定义域为(-1,+∞).
当x∈(-1,0]时,由(1)知f′(x)在(-1,0]上单调递增,又f′(0)=0,所以在(-1,0)上,f′(x)<0,从而f(x)单调递减,又f(0)=0,因此,在(-1,0]上,f(x)有唯一零点,且零点为0.
当x∈[π,+∞)时,因为sinx≤1,ln(x+1)>1,所以f(x)<0,从而f(x)在[π,+∞)上无零点.
综上,f(x)有且仅有2个零点.
点评本题难度较大,第(1)问涉及“二次求导”技巧的应用,同时又引入了函数g′(x)的“隐零点”,便于目标问题的求解;第(2)问需要在明确函数定义域的基础上,灵活运用“分类与整合思想”解题,其中当x∈(0,]时,对函数f(x)的零点情况的分析是难点,需要引入函数f′(x)的“隐零点”,便于突破目标问题.
本文通过归类举例的形式阐明利用导数研究函数的零点问题,有利于强化求导技巧在解题中的灵活运用,巩固“分类与整合思想”“数形结合思想”以及“转化思想”的综合运用,进一步理解、体验函数“隐零点”应用,有助于目标问题的顺利获解.
(完)

