复合函数考查中常见的4类问题
谢永惠
(福建省漳州市龙海区教师进修学校)
复合函数是高考中的必考题目,但因其问题较为复杂,解题具有一定的难度,导致学生在考试中解题效果并不理想,容易出现各种错误.为帮助学生更加全面地掌握复合函数,本文结合实际问题,总结复合函数在考试中的常见题型及解题策略,以促进学生成绩的提升.
1 零点问题
复合函数的零点问题是考试中常见的问题之一,在实际解题中,可以将复合函数中内函数进行换元处理,如将y=g[f(x)]中的内函数换元为t=f(x);而后画出相应的图像,这一过程需进行分类讨论;最后借助数形结合方法解答复合函数的零点问题.
例1已知函数f(x)=-x2-2x,g(x)=若方程g[f(x)]-a=0有4个实数解,求a的取值范围.
解析令t=f(x),则t=f(x)=-x2-2x图像如图1所示.
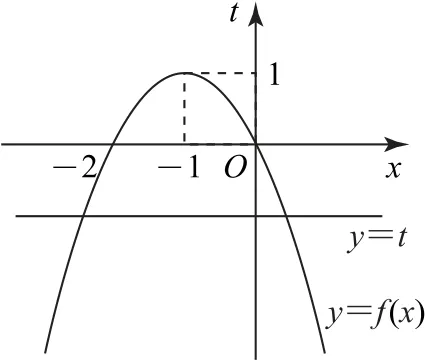
图1
当t>1时,y=t与y=f(x)无交点;
当t=1时,y=t与y=f(x)有1个交点;
当t<1时,y=t与y=f(x)有2个交点.
作出函数a=g(t)的图像,分析y=a与y=g(t)交点横坐标t的取值及范围,得到t=f(x)的交点个数.方程g[f(x)]-a=0,即a=g[f(x)],则可以视为a=g(t),t=f(x)的复合,即
作出a=g(t)的图像,注意到t=-x2-2x≤1,则函数a=g(t)的图像如图2所示.
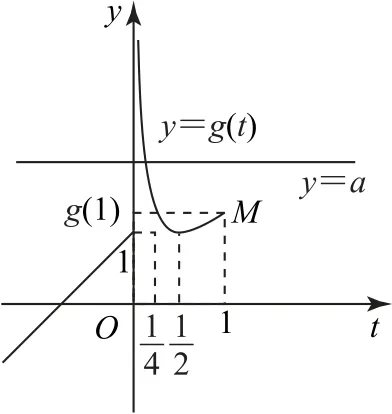
图2
当a>g(1)=时,y=a与y=g(t)有1个交点,此时y=t与y=f(x)有2 个交点,即方程g[f(x)]-a=0有2个实数解,不符合题意.
当a<1时,y=a与y=g(t)有1个交点,此时t<0,即y=t与y=f(x)有2 个交点,即方程g[f(x)]-a=0有2个实数解,不符合题意.
综上,a的取值范围为[1,).
点评g[f(x)]是典型的复合函数,先通过换元令t=f(x),再画出其图像并对t的取值进行分类讨论;而后作出函数a=g(t)的图像,分析y=a与y=g(t)的交点,得到的交点个数,最终解答问题.
2 奇偶性问题
在解答复合函数的奇偶性问题时,需要在关于坐标原点对称的定义域背景下进行分析,同时应当紧紧围绕奇偶性的定义与复合函数“同奇为奇,其他为偶”的特性进行解答问题.
例2是奇函数,a∈R.
(1)求a的值;
(2)对任意x∈(-∞,0),不等式f(2x+1)>log2(m-2x)恒成立,求实数m的取值范围.
点评在解答第(1)问时,需要结合奇函数的定义构建关系式,解方程得到参数值;在解答第(2)问时,需要对不等式进行转化,通过构建函数,利用基本不等式、函数定义域等确定参数的取值范围.
3 单调性问题
单调性是函数的基础性质,因此复合函数的单调性也是常见的考点,其主要考查了学生对函数相关基础知识的掌握情况.在解答这类问题时,还需学生拥有坚实的理论基础,进而结合题目信息逐步解答.
例3函数的单调递增区间是( ).
A.(0,1] B.(-∞,1]
C.(0,+∞) D.[1,+∞)
解析令u(x)=x2-2x+6=(x-1)2+5,则f(x)=()u(x),则u(x)的对称轴为x=1,故u(x)在(-∞,1]上单调递减,在[1,+∞)上单调递增,故f(x)在(-∞,1]上单调递增,在[1,+∞)上单调递减,故选B.
点评在本题解答过程中,首先进行了换元处理,其次通过分析可得到函数u(x)的单调区间;而后根据复合函数“同增异减”的法则,确定答案.
4 参数问题
含参复合函数是参数问题中较为常见的考查方式,在解答这类问题时,学生需要结合实际问题选择合适的方法(如分离参数法、导数法、数形结合法等)快速解题.
例4 已知函数f(x)=aex-1-lnx+lna,若f(x)≥1,求a的取值范围.
解析当0<a<1时,f(1)=a+lna<1.
当a=1时,f(x)=ex-1-lnx,则f′(x)=当x∈(0,1)时,f′(x)<0,f(x)单调递减,当x∈(1,+∞)时,f′(x)>0,f(x)单调递增.因此,当x=1时,f(x)取得最小值,为fmin(x)=f(1)=1,从而f(x)≥1.
当a>1时,f(x)=aex-1-lnx+lna>ex-1-lnx≥x-1+1-(x-1)=1.
综上,a的取值范围是[1,+∞).
点评在解答本题过程中,借助了导函数思维,通过导函数将不等式问题转化为了单调性与极值问题,从而使学生快速解答问题.
本文总结了对复合函数考查过程中常见的零点问题、奇偶性问题、单调性问题及参数问题及其常用的解题方法,以帮助学生找准复习方向,提高成绩.
(完)

