对2023年数学新高考Ⅰ卷的试题评析与备考策略

范明辉

(湖北省荆门市龙泉中学)

2023年,对于使用数学新高考Ⅰ卷的省份而言,是新课标、新教材、新高考“三新”背景交会统一的开局之年.新高考Ⅰ卷数学试题在“反套路”“反机械刷题”上下足了功夫,突出了试题的基础性、综合性、应用性和创新性的考查要求,体现了数学学科在人才选拔中的重要作用,同时也为今后的复习备考和数学学习指明了方向.

1 考查维度

2023年数学新高考Ⅰ卷逐题多维度考查细目如表1所示.

表1

2 试题评析

2.1 基础性

2023年数学新高考Ⅰ卷第5,7,9,11,16,20,21,22题重点考查了高中数学基本概念,第2,3,4,8,10,13,14,17,21对高中数学基本公式、基本原理进行了考查,突出了试题的基础性,考查学生对于必备知识的掌握情况.

例1(2023 年新高考Ⅰ卷4)设函数f(x)＝2x(x－a)在(0,1)上单调递减,则a的取值范围是( ).

A.(－∞,－2] B.[－2,0)

C.(0,2] D.[2,＋∞)

分析本题属于课程学习情境,以指数型复合函数的单调性为载体,考查逻辑思维能力和运算求解能力.借助复合函数“同增异减”的单调性判定法则,将原问题转化为二次函数y＝x(x－a)在(0,1)上单调递减的问题,或直接求导处理,将原问题转化为导函数在(0,1)上小于或等于零恒成立问题.

解法1函数y＝2x在R 上单调递增,而函数f(x)＝2x(x－a)在(0,1)上单调递减,由复合函数的单调性法则,可知函数y＝x(x－a)在(0,1)上单调递减,故对称轴,即a≥2,故选D.

解法2因为函数f(x)＝2x(x－a)在(0,1)上单调递减,所以f′(x)＝2x(x－a)·(2x－a)·ln2≤0在(0,1)上恒成立,则2x－a≤0 在(0,1)上恒成立,所以a≥2x,又2x＜2,则a≥2,故选D.

例2(2023 年新高考Ⅰ卷14)在正四棱台ABCD-A1B1C1D1中,AB＝2,A1B1＝1,AA1＝,则该棱台的体积为________.

分析本题属于课程学习情境,以正四棱台的体积为载体,考查运算求解能力.《普通高中数学课程标准(2017 年版2020 年修订)》中指出,“要知道球、棱柱、棱锥、棱台的表面积和体积计算公式,能用公式解决简单的实际问题”.自2021年以来,高考数学试题这几年都对台体的体积进行了考查,其目的并不是考查学生对于台体体积公式的机械记忆,而是要让大家从台体的形成过程出发,回到台体的定义,“还台为锥”,借助锥体的体积得到台体的体积,从本质上理解并掌握台体体积的计算公式.

图1

2.2 综合性

2023年数学新高考Ⅰ卷第6,7,8,11,12,16,17,18,19,20,21,22题突出考查高中数学知识内部的联系,在知识的交会处命题,凸显了各模块之间的联系,强调学生要注重知识的本质,能够融会贯通,灵活运用,形成完整的高中数学知识体系.

例3(2023年新高考Ⅰ卷6)过点(0,－2)与圆x2＋y2－4x－1＝0相切的两条直线的夹角为α,则sinα＝( ).

分析本题属于课程学习情境,以过圆外一点作圆的切线问题为载体,考查逻辑思维能力和运算求解能力.过圆外一点作圆的切线问题是一种常见的出题背景,新人教A 版高中数学《选择性必修第一册》第92页便有一道这样的例题(课本中的例2),而这道高考题在学生熟悉的背景中再次创新,考查三角求值问题,体现试题的综合性,对学生的综合运用能力有一定的要求.

解如图2所示,记点P(0,－2),两条切线分别为PA,PB,与圆M相切于A,B两点,连接MA,MB,MP和AB,记AB与MP相交于点C.

易知切点弦AB所在的直线方程为2x＋2y＋1＝0,所以,由勾股定理易求得

例4(2023年新高考Ⅰ卷19)已知函数f(x)＝a(ex＋a)－x.

(1)讨论f(x)的单调性;

分析本题属于课程学习情境,以函数单调性的讨论、含参数不等式的证明为载体,考查逻辑思维能力和运算求解能力.试题设问较为常见,但一改往年的命题风格,题序前移,难度也随之降低到了课本习题难度.这无疑释放出了两个信号:

1)高考解答题的顺序不会一成不变,任何模块都可能成为压轴题;

2)复习时要重视教材中出现的例题、习题,高考题的考查情境很大程度上来源于教材.考生必须对每个模块都加以重视,认真学习,要树立拿满分的目标.

解(1)易 知f′(x)＝aex－1,当a≤0 时,f′(x)＜0,所以f(x)在R 上单调递减;当a＞0时,令f′(x)＞0,可得x＞－lna;令f′(x)＜0,可得x＜－lna,所以f(x)在(－∞,－lna)上单调递减,在(－lna,＋∞)上单调递增.

解法2记g(x)＝ex－x－1,则g′(x)＝ex－1,所以当x＜0时,g′(x)＜0,当x＞0时,g′(x)＞0,则g(x)在(－∞,0)上单调递减,在(0,＋∞)上单调递增,所以g(x)≥g(0)＝0.又

2.3 应用性

2023年数学新高考Ⅰ卷第10,13,21题设置生活实践情境,将抽象的数学概念与实际生活相结合,体现了数学的应用性,强调学生要注重理论联系实际,活学活用,考查学生运用数学知识分析和解决实际问题的能力.

例5(2023年新高考Ⅰ卷10,多选题)噪声污染问题越来越受到重视.用声压级来度量声音的强弱,定义声压级,其中常数p0(p0＞0)是听觉下限阈值,p是实际声压.表2 为不同声源的声压级.

表2

已知在距离燃油汽车、混合动力汽车、电动汽车10m 处测得实际声压分别为p1,p2,p3,则( ).

A.p1≥p2B.p2＞10p3

C.p3＝100p0D.p1≤100p2

分析本题属于生活实践情境,以噪声污染问题为背景,以对数运算为载体,考查运算求解能力.解决此题的主要难点在于提取表格数据信息,结合声压级的定义和对数运算法则,正确运算出四个选项内容中的代数关系.试题是在新人教A 版高中数学《必修第一册》第141页习题4.4第10题的基础上创新了设问方式,改变了题型,将高中数学中的对数知识和不等式内容与实际生活相结合,在考查学生数学运算功底的同时,也充分发挥了试题的德育功能,引导学生注意保护环境.

例6(2023年新高考Ⅰ卷21)甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若未命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为0.6,乙每次投篮的命中率均为0.8.由抽签确定第1次投篮的人选,第1次投篮的人是甲、乙的概率各为0.5.

(1)求第2次投篮的人是乙的概率;

(2)求第i次投篮的人是甲的概率;

(3)已知:若随机变量Xi服从两点分布,且P(Xi＝1)＝1－P(Xi＝0)＝qi(i＝1,2,…,n),则记前n次(即从第1次到第n次投篮)中甲投篮的次数为Y,求E(Y).

分析本题属于生活实践情境,以投篮这种学生熟悉的生活情境为背景,以概率与统计为载体,考查逻辑思维能力、运算求解能力和数学建模能力.试题第(1)问考查新人教A 版高中数学教材新增内容“全概率公式”的应用;第(2)问要求学生能够发现投篮规律,构建等比数列模型,运用等比数列的相关知识运算求解.对于此类问题的求解,在新人教A 版高中数学《选择性必修第二册》第39 页例12、第41 页习题4.3第8题中皆有体现.第(3)问结合两点分布模型,与第(2)问环环相扣,需要将其转化为数列求和问题.试题引入投篮问题,意在引导学生要加强体育锻炼,注重劳逸结合.

解记“第i次投篮的人是甲”为事件Ai,“第i次投篮的人是乙”为事件Bi.设P(Ai－1)＝pi－1(i＝1,2,…,n),则P(Bi－1)＝1－pi－1.

(1)由题意可得P(B2|A1)＝1－0.6＝0.4,P(B2|B1)＝0.8,由全概率公式得

2.4 创新性

2023年数学新高考Ⅰ卷第6,11,12,21,22题凸显了试题的创新性,探索了新的设问方式,强调学生要灵活运用所学知识,考查学生的探究意识和创新能力,为全面提高人才自主培养质量,着力造就拔尖创新人才助力.

例7(2023 年新高考Ⅰ卷11,多选题)已知函数f(x)的定义域为R,f(xy)＝y2f(x)＋x2f(y),则( ).

A.f(0)＝0

B.f(1)＝0

C.f(x)是偶函数

D.x＝0为f(x)的极小值点

分析本题属于探索创新情境,以抽象函数及其性质为载体,考查逻辑思维能力、运算求解能力、数学建模能力和创新能力.对于A,B,C 选项,可采用赋值法解决,难点在于C 选项,判断函数的奇偶性需从定义入手,找到f(－x)与f(x)之间的关系.由于等式右边f(x)的系数为y2,等式左侧为f(xy),考虑令y＝－1,将奇偶性的判定问题转化为求f(－1)的值.至于D 选项,可以构造符合题意的特殊函数,利用函数模型加以解决.

解令x＝y＝0,得f(0)＝0,故A 正确.令x＝y＝1,得f(1)＝f(1)＋f(1),所以f(1)＝0,故B正确.令x＝y＝－1,可得f(1)＝f(－1)＋f(－1)＝0,所以f(－1)＝0;令y＝－1,可得

所以f(x)是偶函数,故C正确.

对于D,考虑常函数f(x)＝0满足题设条件,但函数f(x)无极值点,故D 错误.

易知f(x)在(0,)上单调递减,在,＋∞)上单调递增.纵观整个定义域,可知x＝0为f(x)的极大值点,故D 错误.

综上,选ABC.

例8(2023年新高考Ⅰ卷12,多选题)下列物体中,能够被整体放入棱长为1m 的正方体容器(容器壁厚度忽略不计)内的有( ).

A.直径为0.99m 的球体

B.所有棱长均为1.4m 的四面体

C.底面直径为0.01m、高为1.8m 的圆柱体

D.底面直径为1.2m、高为0.01m 的圆柱体

分析本题属于探索创新情境,以正方体、球、正四面体、圆柱体等常见的几何体为载体,考查逻辑思维能力、运算求解能力和空间想象能力.试题以学生熟悉的多面体和旋转体为背景,考查学生对这些几何体基本特征的掌握情况,同时创新设问方式,对考生的空间想象能力要求较高.值得注意的是,对于D 选项,不能简单地通过圆柱体的底面直径1.2 m 小于正方体的体对角线长度m,就认为可将整个圆柱体放入正方体之中,而是要从整体上考虑.

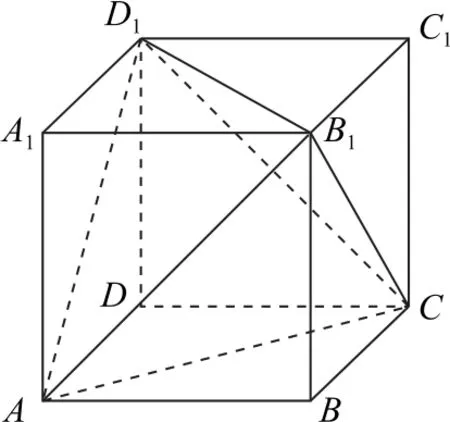
图3

对于D 选项,首先需要说明的是圆柱体的底面或中截面能够放入正方体中.如图4所示,作出正方体中与体对角线A1C垂直且经过正方体中心O的正六边形截面EFGHIJ.

图4

在《普通高中数学课程标准(2017年版2020年修订)》的附录案例11正方体截面的探究中,可以探究发现此正六边形截面为正方体内面积最大的截面,易求得正六边形截面EFGHIJ的内切圆直径d＝,因此可在这个正六边形中可以放入一个以O为圆心,直径为1.2m 的圆.

接下来需要说明整个圆柱都可以放进去.如图5所示,在正六边形截面中过点O作正方体体对角线A1C的垂线交EF于点M,在线段OM上取点P,使得OP＝0.6m,过点P作体对角线A1C的平行线交A1M于点Q,连接PQ.

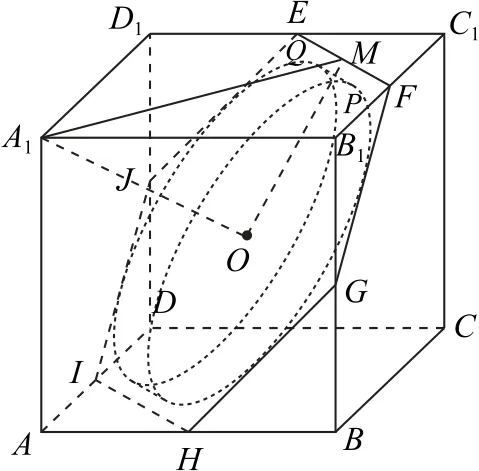
图5

因此,正方体内可以放入直径为1.2 m、高为0.03 m的圆柱体,故D 正确.

综上,选ABD.

3 备考策略

1)潜心研究真题,找准备考方向

高考真题是学生备考的重要参照,必须要潜下心来,认真研究.高中数学知识内容繁多,不同知识的学习目标和要求不尽相同,究竟哪些内容应当予以了解,一带而过,哪些内容应当深入探究,拓展推广,这需要根据历年高考真题的考查特点找到备考方向,而不是盲目地进行扩充.2023 年数学新高考Ⅰ卷第12题是个很好的例子,以正方体为载体,看似简单,实则颇有难度.不同于日常训练时“正方体问题建系处理”的情形,此题无法很好地借助空间直角坐标系来解决,需要较强的空间想象能力.这种能力的培养,是一个长期的过程,而类似于《普通高中数学课程标准(2017年版2020年修订)》附录中的案例11就是很好的学习素材.因此,潜心研究高考真题是非常必要的.

2)静心钻研教材,挖掘习题功能

教材是学生学习数学的基本参照.我们要用教材学,而不是简单地“学教材”.在学习新知识的过程中,学生要领会教材的编写意图,以适当的方式用好教材.对于教材中的重要概念,要精心研读,提炼出概念中所蕴含的数学思想方法.对于习题的处理,要充分挖掘教材中典型例题、习题的功能,注重“一题多解”和“一题多变”,从多角度看待问题,把握问题的本质.通过改编教材例题、习题而生成高考试题的例子比比皆是,教材的重要性不言而喻.

3)用心参与课堂,注重思想方法

课堂是学生收获知识的主要阵地.在有限的时间里,高效地开展课堂学习显得尤为重要.这就需要学生在课前进行预习,发现和提出问题,带着自己的疑问去听课,积极与老师进行互动,真正地参与课堂学习.新时代背景下,国家需要的不是只会考试的人,而是会解决问题的人.这就要求学生在日常学习中,要注重思想方法的领会,而不是专注于考试的解题技巧.2023年数学新高考Ⅰ卷中对于数列求和问题的考查,不同于以往的“错位相减”“裂项相消”题型,而是与概率统计内容有机结合,需要学生运用数列的递推思想,自主探索,这不是机械地训练解题技巧就能应付的.

4)真心交流互动,提高思维品质

互动是学生检验自我的重要途径.只有主动参与数学学习,积极与同学、老师进行交流、讨论、互相切磋,才能激发自己的学习兴趣,提高数学思维品质,不断体会到学习数学时无与伦比的成就感.将自己的解题方法、解题思路讲给老师、同学听,同时听取他人的想法,是一种非常好的交流互动方式.它能够帮助我们意识到自己哪些地方掌握得比较好、哪些地方还存在着不足.通过不断进步、不断收获学习数学的成就感,学生才会产生强大的动力去面对数学学习中的困难,敢于直面数学挑战.从2023年数学新高考Ⅰ卷的考查情况来看,“刷题式”学习越来越无法让学生在高考数学中脱颖而出,而提高学生的数学思维品质,让学生学会分析问题、解决问题才是未来决胜于高考考场的必胜法宝.

(完)