气动齿状软体驱动器的理论建模、仿真分析及实验研究

苏怡仪, 徐齐平, 刘锦阳

(1. 上海交通大学 工程力学系, 上海 200240; 2. 浙江师范大学 工学院, 浙江 金华 321004)

软体机器人不同于由硬材料制成的、用于精确重复工作的传统刚性机器人,其完全由低阻抗的软材料(如形状记忆合金(SMA)、介电弹性体(DE)、硅胶、水凝胶等)制成[1],能够适应未知环境,产生连续变形并吸收碰撞和接触所产生的能量,具有高度的灵活性、敏感性、安全性和环境适应性,能够实现扭转、爬行、抓取等操作目标,在医疗保健、野外探索和人机交互领域具有广泛的应用前景[2].目前,软体机器人的主要驱动方式包括流体驱动、形状记忆合金驱动及电活性聚合物驱动等[3].其中,气动软体驱动器以其质量小、安全、成本低、易于制造等优点而得到广泛应用.

一般来说,气动软体驱动器由各向同性弹性材料制成,在结构中嵌入一个或多个腔室,气腔与气管相连通.其结构具有各项异性,通过向密闭腔室充气或放气改变腔室内气压,从而使软体驱动器产生弯曲、爬行等变形运动.根据各向异性结构的不同,气动软体驱动器一般可分为两类:纤维增强气动软体驱动器和气动齿状软体驱动器.纤维增强气动软体驱动器一般由一个空心弹性体腔室组成,沿驱动器的长度方向排列螺旋状纤维以约束径向变形,施加气压的能量主要用于产生弯曲变形,这类纤维增强气动软体驱动器的研究可以追溯到McKibben人工肌肉[4].另外,气动齿状软体驱动器是一种新型的驱动器,它的外形为齿状,每个齿状结构内嵌一个腔室,腔室的侧壁往往设计得较薄,充气之后,腔室的侧壁膨胀,并且互相接触、挤压,从而产生比纤维增强气动软体驱动器更大的弯曲曲率和更大的夹持力.通过改变齿状结构与驱动器轴线的夹角,还能产生复杂的扭转运动,这种螺旋状的构型能够紧紧地缠绕住物体,抓持更加可靠,还能够穿越复杂的狭小空间;通过独立控制每个气腔的气压,气动齿状软体驱动器表现出超强的灵活性;此外,气动齿状软体驱动器广泛应用于抓取和爬行.因此,对气动齿状软体驱动器进行理论、仿真、实验研究,具有深远的应用价值.

由于软体机器人具有无限的自由度[5],刚性机器人的建模方法无法适用,研究者只能对力学模型做适当合理的简化,力求用最少的自由度描述软体机器人的运动.目前针对软体驱动器的建模大都基于底层不可伸长的恒定曲率假设,结合几何关系或者等效力原理推导出驱动气压和输出角度之间的关系.Polygerinos等[6]利用Ecoflex-0030硅胶制造了纤维增强气动软体机器人,基于Neo-Hookean材料模型,利用弯矩平衡原理,推导出了输入气压和驱动器弯曲角度之间的关系,并在有限元软件Abaqus中得到了验证;Gu等[7]基于最小势能法和连续杆理论,结合几何复杂性和材料弹性,提出了一类具有弯曲和扭转变形的气动网络软体驱动器(gPNSAs)的运动学模型,研究了几何参数、材料性质和外力对gPNSAs变形的影响;Alici等[8]将以卷尺为代表的双稳态柔性薄金属纳入执行机构的拓扑结构中,以防止执行机构在垂直面上运行时在自身质量下发生偏转,基于等曲率假设和等效力平衡,推导了驱动器的弯曲角度和阻塞力与输入压力之间的关系,并进行了实验验证;Wang等[9]结合几何关系和材料弹性,建立了具有最小摩擦功能原理的模块化差速驱动软体机器人(MDDSR)爬行运动的非线性状态空间运动学模型,并考虑了充气气压与体积之间的耦合关系;Zhong等[10]利用弹性体材料的定容原理,将气动网络软体驱动器的多个离散腔室等效为连续介质驱动器中的单个腔室,以预测软体驱动器的弯曲角度和尖端接触力;De Payrebrune等[11]基于欧拉弹性杆理论,在齿状驱动器末端施加作用力,推导出了变曲率运动学模型.

为了改进仿真计算精度,一些学者基于绝对节点坐标法对软体机器人的力学建模进行研究.Shabana等[12]利用绝对节点坐标法,推导了恒定气压力对应的广义力形式,并利用Nanson公式来解释表面几何形状的变化对驱动压力的影响;徐齐平等[13]以气动软体驱动器作为研究对象,基于绝对节点坐标法的实体单元和Yeoh本构模型对该驱动器及其演化的单肢软体爬行机器人进行力学建模和数值仿真,等比例模拟软体机器人的整体运动变形情况.

总体来说,软体驱动器的准静态建模研究还存在着以下问题:① 理论模型做了大量的简化和假定,例如,用线弹性理论替代超弹性不可压缩软材料的本构模型,假定模型底层不可伸长,根据结构特点只考虑底层或腔室侧壁的应变能,这类模型由于系统的应变能表达式不完整,精度较低且不具有适用性;② 基于绝对节点坐标法建立的理论模型比较复杂,存在着计算效率低,难以进一步开展优化控制研究等问题;③ 对驱动器与环境发生交互作用时的变曲率问题研究较少.

本文针对气动齿状软体驱动器,以腔室侧壁膨胀角和驱动器弯曲角度为位形坐标,建立了非线性的约束关系,用虚功原理建立了软体驱动器的准静态模型.该模型的特点是同时考虑了底层、侧壁和前后壁的应变能,相较于传统的考虑局部应变能的力学模型,具有较高的精度.对气压作用下固支-自由的软体驱动器的弯曲变形进行了仿真分析,通过Abaqus有限元仿真和静力学实验验证了理论模型的可行性.将单个气腔的分段等曲率建模方法应用于固支-末端受载荷的驱动器上,所得弯曲变形构型与Abaqus的模拟结果基本一致.该模型兼顾精确性和效率,对软体驱动器的设计和运动分析具有一定指导意义和参考价值.

1 气动齿状软体驱动器的结构设计

本文研究的气动齿状软体驱动器的结构和参数如图1所示,它由上部气腔层和底层组成.上部气腔层由9个离散气腔线性排列构成,也称为气动网络,各个气腔之间由一个2 mm宽、2 mm高的内部通道连通,剖面图显示了清晰的内部结构.图中:驱动器的总长度L=78 mm;总宽度l=20 mm;总高度H=17 mm;相邻气腔的外部间隙d=2 mm;气腔外部宽度t=6 mm;气腔内部宽度a=4 mm;气腔侧壁厚度h=1 mm;气腔上壁厚度、底层厚度和内部通道高度均为c=2 mm;内部通道的内顶面到外顶面的距离f=1 mm;内部通道的内底面到外顶面的距离k=3 mm;内部通道的外顶面到气腔内部顶面的距离b=10 mm.当驱动器充气时,气腔的侧壁会发生明显膨胀变形,相互接触、挤压,致使底层产生弯曲变形.当撤去外加气压时,由于硅胶材料的超弹性和柔顺性,驱动器很容易恢复原状.

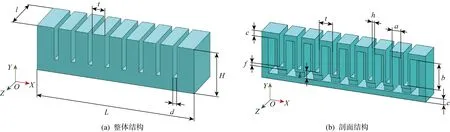
图1 气动齿状软体驱动器的结构Fig.1 Structure of pneumatic toothed soft actuator

采用3D打印技术制作模具(见图2),模具由上部气腔模具和底层模具两部分组成.气动齿状软体驱动器的制备过程如下.

(1) 选用Dragon Skin 30硅胶材料,将A、B两种组分按1∶1的比例混合,利用搅拌机快速搅拌均匀.

(2) 用凡士林均匀涂抹在模具表面,有利于后续脱模.

(3) 将模具1和模具2上下装配在一起,形成上部气腔模具.将配置好的硅胶材料均匀注入上部气腔模具中,长而细的硅胶流有利于防止气泡的积聚.应填充足够的硅胶使它吞没内部的模具,在充分沉淀后,利用刀片刮除多余的硅胶.用真空泵抽气5 min,有利于硅胶沉淀和排除气泡.

(4) 放入60 ℃恒温箱中干燥30 min,缓慢拔除模具,得到上部气腔层.模具2凸起的9个矩形方块和8个小正方块分别形成气腔腔室和内部通道,模具2凹陷的16个小矩形方块形成上部气腔的一组“脚”.

(5) 用皮带冲在上部气腔层的左端面打出一个直径为2 mm的孔,将直径为3 mm的聚氯乙烯(PVC)软管插入孔中,利用硅胶黏合剂将接口的两侧密封.

(6) 将配置好的硅胶材料缓慢、 均匀注入底层模具3中,用真空泵抽气5 min.将上部气腔层置于底层模具上,放入60 ℃恒温箱中干燥30 min,缓慢拔除模具,得到气动齿状软体驱动器的实体.

(7) 将气动齿状软体驱动器放入水池中,利用气泵缓慢充气,观察是否有气泡逸出,检查气密性.

2 气动齿状软体驱动器的分段等曲率理论建模

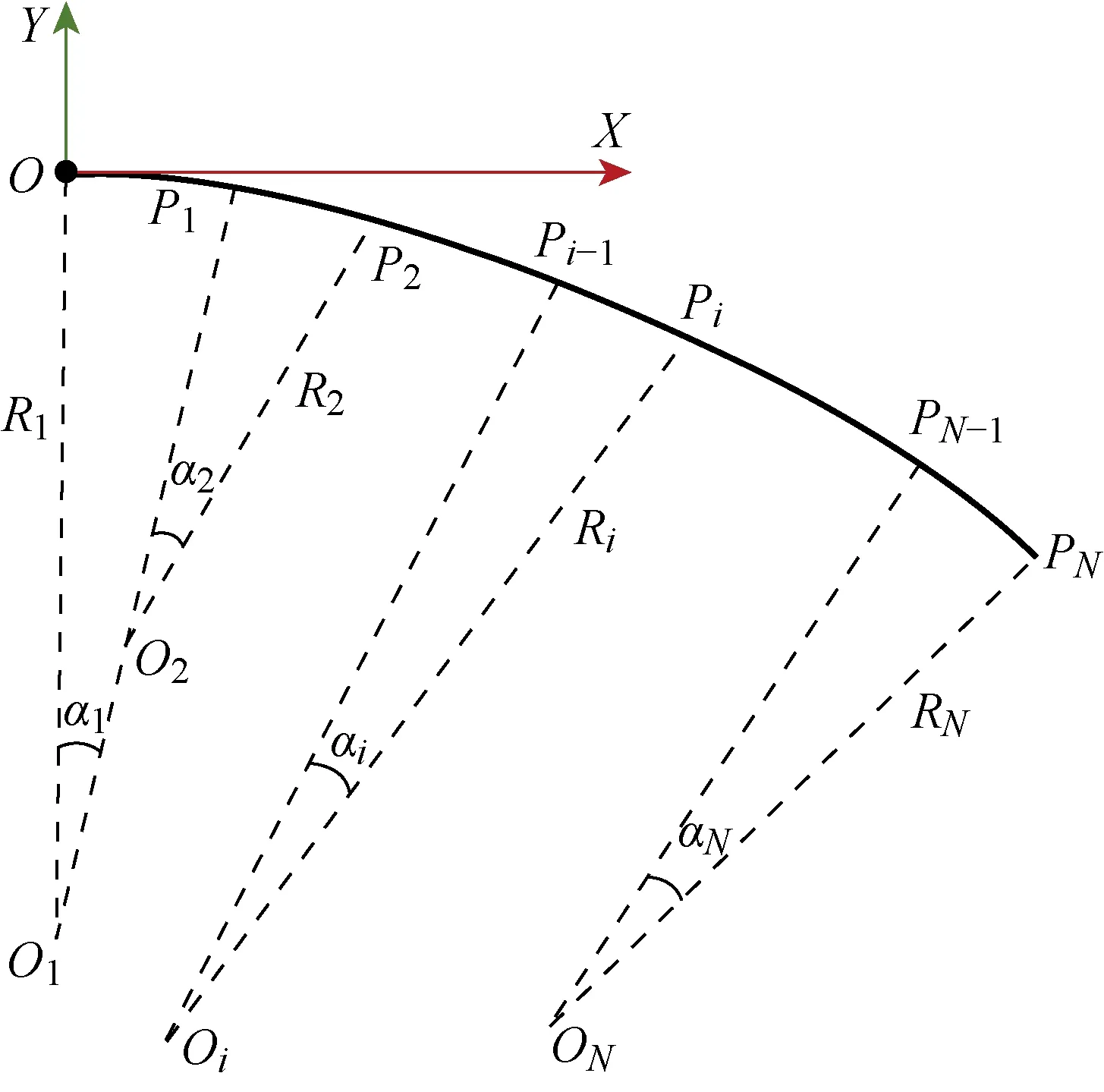
图3 软体驱动器的底层构型示意图Fig.3 Configuration of bottom surface of soft actuator

设第i个气腔的底层的左端点Pi-1和右端点Pi的坐标分别为(xi-1,yi-1)和(xi,yi),它们之间的递推关系为

x0=y0=0

(1)

(2)

(3)

(4)

式中:i=3, 4, …,N.

2.1 单个气腔的等曲率模型

对软体驱动器的第i个气腔进行非线性变形分析,以确定其弯曲角度与充气气压之间的关系.在该分析中,涉及3个非线性关系:① 硅胶材料的非线性应力-应变关系;② 充气压力p与第i个气腔的腔室侧壁膨胀角θi之间的关系;③θi与αi之间的关系.

为了建立准确而高效的模型,基于Abaqus仿真和实验结果给出以下5个假定.

(1) 如图4(a)和4(b)所示,气腔在未充气时为矩形;充气时,腔室的侧部膨胀呈圆弧曲面,两个侧面发生接触,如图4(c)所示.图中:气腔前后壁厚度e=2 mm.

(2) 与侧壁相比,上壁和前后壁的变形要小得多,因此在充气过程中,腔室高度b恒定.

(3) 充气时,软体驱动器的最底层无伸长缩短,整体变形形状呈圆弧形.

(4) 对于超弹性不可压缩材料,必须满足λ1λ2λ3=1.以图1所示的整体坐标系为基准,λ1为沿底层弧长方向的主拉伸比,λ2为沿Y轴方向的主拉伸比,λ3为沿Z轴方向的主拉伸比.对于软体驱动器,λ3=1,则λ2=1/λ1.

(5) 软体驱动器前后壁的应力和应变分布有相同的集中区域,且在该区域内,存在一对称轴,使得应变能关于该轴对称,且线性分布.

2.1.1几何关系 本文设计的软体驱动器由N=9个相同大小的气腔组成,图4(a)和4(b)为未充气状态下的两个相邻气腔的顶部和前横截面视图,图4(c)为充气状态下的两个相邻气腔的前横截面视图.

基于上述假定,以第i(i=1, 2, …, 9)个气腔为研究对象,气腔的底层长度Li0与弯曲角度αi存在以下关系:

L0i=Riαi

(5)

同理,充气后,第i个气腔中心线的长度为

(6)

由图4(a)和4(b)可知,每个气腔的底层长度为

(7)

第i个气腔中心线与其底层长度的关系为

(8)

由式(6)～(8)可以得到θi与αi之间的非线性关系:

(9)

对式(9)求偏导,得到:

(10)

2.1.2底层应变能 硅胶材料可以被建模为不可压缩的Neo-Hookean材料,应变能的表达式为

(11)

式中:Ve为积分区域的体积;由硅胶材料的单轴拉伸实验[14]获得切变模量G=0.484 MPa.

对于第i个气腔底部的任意一层,其长度为

Li(z)=(Ri+z)αi

(12)

式中:z为该层到最底层的距离.该层沿弧长方向、厚度方向和Z方向的主拉伸比为

(13)

(14)

对于一个气腔单元,底层分为两部分:第1部分的厚度为c1=c,长度为L1=a;第2部分的厚度为c2=c+k,长度为L2=d+2h.下面分别对两部分的应变能进行计算.

第1部分和第2部分的应变能分别为

(15)

(16)

将式(13)代入式(15)和(16)并积分,得到:

(17)

(18)

第i个气腔底层的总应变能为

(19)

将式(5)代入式(17)和(18)并对αi求偏导,得到:

(20)

式中:

对腔室侧壁膨胀角θi求偏导,得到:

(21)

式中:∂αi/∂θi由式(10)给出.

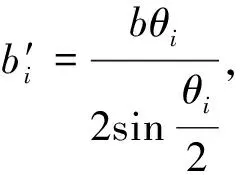
(22)

第i个气腔的侧壁应变能为

(23)

将上式对腔室侧壁膨胀角θi求偏导,得到:

(24)

2.1.4前后壁应变能 通过Abaqus有限元仿真和实验研究发现,软体驱动器气腔的前后壁存在应力和应变的集中区域,该区域高度为mi,宽度为a.在该区域内,存在一对称轴,应变能关于该轴对称,且线性分布.该对称轴到最底层的距离为c+k,在对称轴上应变能最大,该区域的底部和上边界的应变能最小,趋于0.第i个气腔的前/后壁的应变能为

(25)

第i个气腔前后壁的总应变能为

(26)

其中,对称轴上各点的主拉伸比为

(27)

式中:n=(c+k)/a.将式(26)对腔室侧壁膨胀角θi求偏导,得到:

(28)

2.1.5气压力的虚功 每个气腔腔室原始的体积为

V0i=a(b+k)(l-2e)

(29)

变形后的体积为

(30)

气压力所做的虚功为

δWip=pδVi

(31)

将上式对腔室侧壁膨胀角θi求偏导,得到:

(32)

2.2 系统准静态方程的建立

系统的姿态可以由N个独立的广义坐标描述:

(33)

取各腔室侧壁膨胀角θi为广义坐标,多气腔软体驱动器的应变能为

(34)

气压力总的虚功为

(35)

由式(1)～(4)可知,端点PN的位置坐标阵为

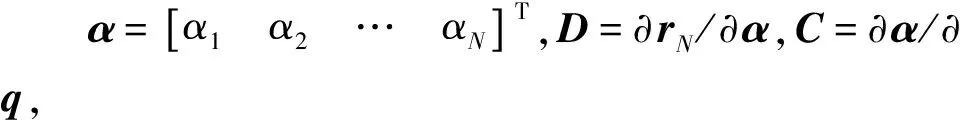
δrN=DCδq

(36)

作用于驱动器末端的载荷F所做的虚功为

(37)

式中:QF为载荷F的广义力,

由虚功原理,得到多气腔软体驱动器的变分方程为

δE=δWp+δWF

(38)

也可写成:

(39)

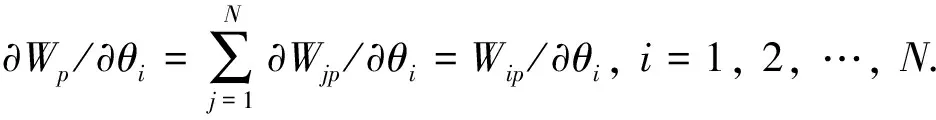
软体驱动器受气压作用自由弯曲的构型如图5所示.当软体驱动器受气压作用自由弯曲时,每个气腔的变形情况具有高度的一致性,即θi、αi、Ri均相同,整个驱动器底层的每一段的曲率均相等,为光滑圆弧状.软体驱动器弯曲角度α为

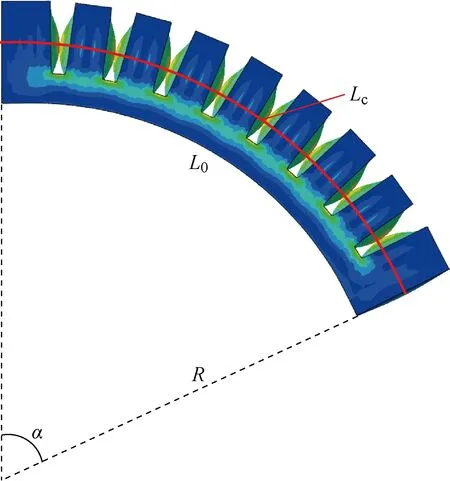
图5 软体驱动器的弯曲形状Fig.5 Curved shape of soft actuator

α=Nαi

(40)

驱动器的底层长度L0和中心线长度Lc与弯曲角度α存在以下关系:

(41)

3 有限元仿真模型

有限元模型能够真实描述系统非线性响应,将应力和应变进行可视化输出,有利于分析局部应力和应变对全局驱动器性能的影响,指导理论建模和设计优化.

3.1 仿真模型的建立

为了对气动齿状软体驱动器的变形行为进行建模,在Solidworks中建立三维模型并将其导入Abaqus/Standard进行有限元分析.将有限元模型的简化降至最低,以便与实验情况接近.左端面的充气入口忽略不计,内部通道考虑在内.模型的所有内壁都施加了均匀的气压力p.将左端面完全固定.在驱动器的底层添加一个厚度为0.1 mm的限制层以限制底层拉伸变形.采用实心20结点二次六面体单元(Abaqus element type C3D20RH)对驱动器的所有部件进行建模,全局种子的近似全局尺寸为1,图6显示了驱动器有限元离散情况,划分单元的总数为 13 704 个.采用静力通用分析步对模型进行分析,同时打开几何非线性开关.

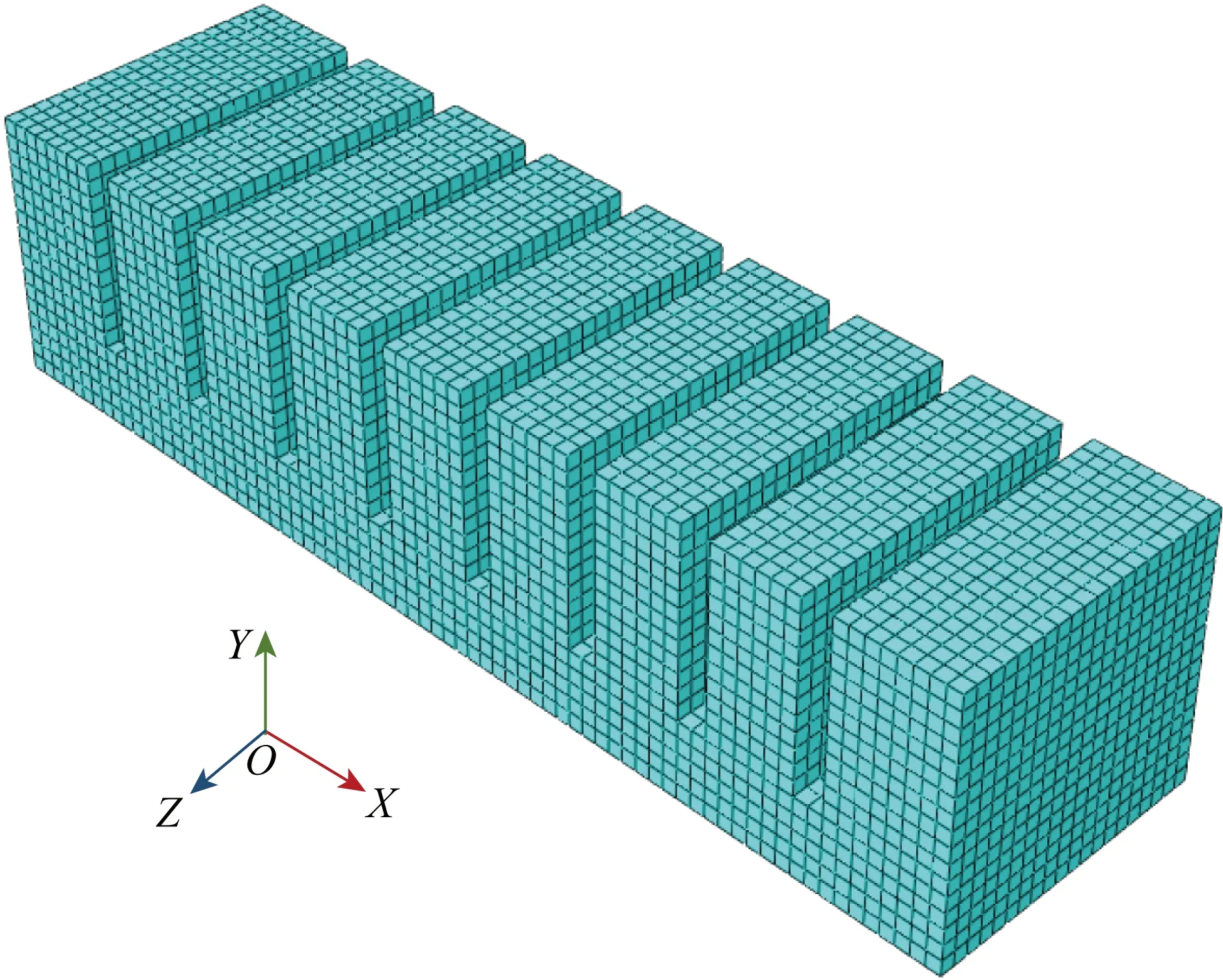
图6 气动齿状软体驱动器有限元离散Fig.6 Finite element discretization for pneumatic toothed soft actuator

3.2 仿真结果和分析

所建立的有限元模型的计算结果(von Mises应力σ分布)如图7所示.从图中可以看出,在驱动气压的作用下,软体驱动器在XOY二维平面内产生弯曲变形,弯曲的轮廓形状为圆弧形,随着气压的增大,弯曲角度逐渐增大.此外,图中显示,应力集中主要发生在连接相邻两气腔的根部区域,主要是由于气腔膨胀之后带动其产生较大的拉伸变形,可以适当增厚以加强结构强度,但不宜过厚,否则输出弯曲角度会大幅减小.气腔侧壁的应变能也比较大,且鼓出的形状为圆弧曲面,曲面两两相切.由于每个气腔的变形状态和应力分布呈现出高度的一致性,在计算应变能时可以取一个气腔为研究对象,再将单个气腔的应变能乘以气腔个数.

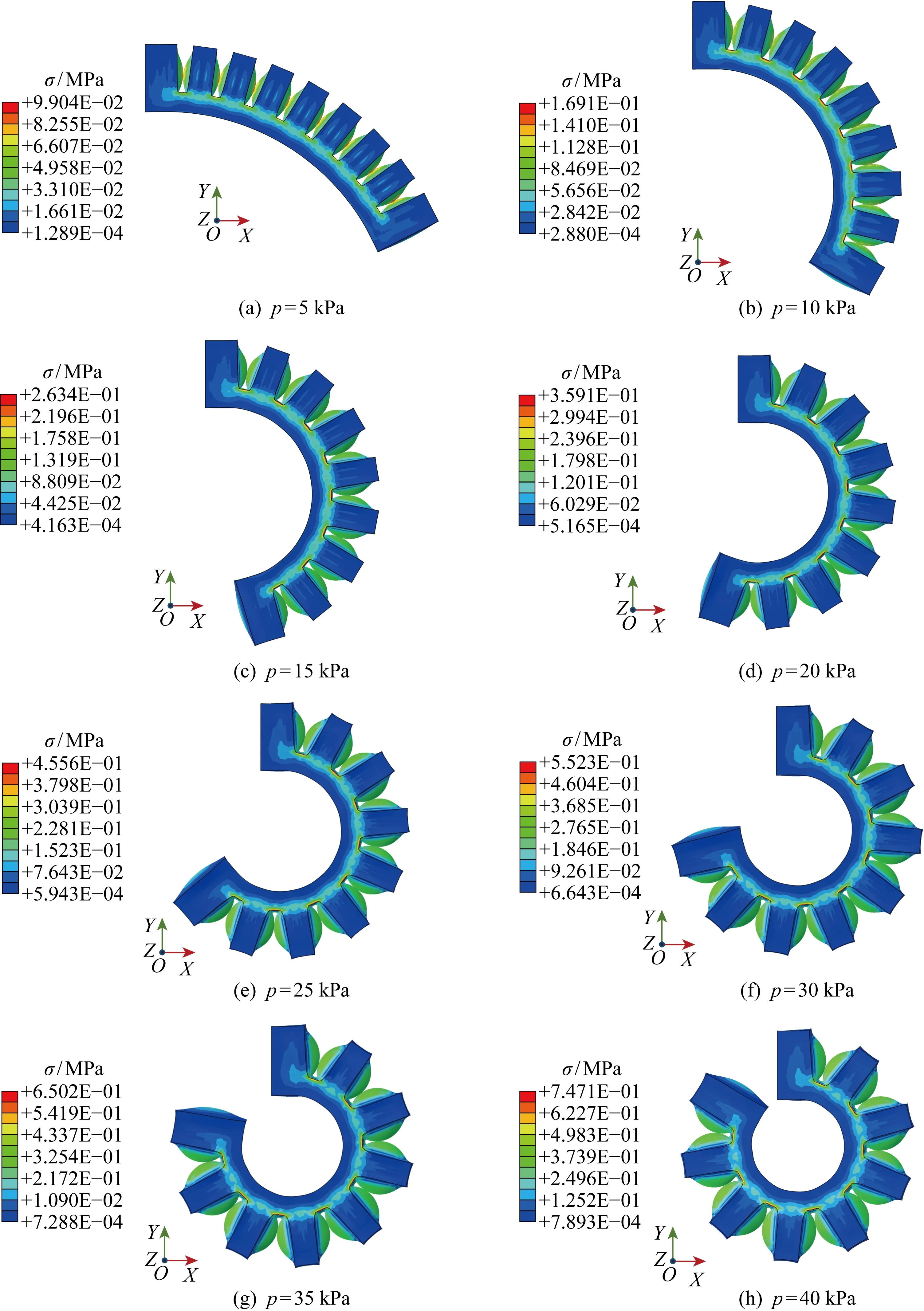
图7 有限元模型的计算结果(von Mises应力分布)Fig.7 Results of Finite element model (von Mises stress distribution)

取一个气腔为研究对象,当气压值p=35 kPa时,von Mises应力σ和应变ε局部分布情况如图8所示.前后壁的应力和应变的区域为红框所示,宽度为a,高度为m,对称轴到最底层的距离为c+k,且局部von Mises应力关于对称轴对称线性分布,而应变在区域内均匀分布,因此应变能关于对称轴对称线性分布,与理论建模中的假定(5)一致.可将对称轴处的主拉伸表达式(27)代入式(25)计算前后壁的总应变能,积分区域为红框所示.此外,最顶层的应力、应变几乎为0,应变能可忽略不计,腔室高度基本恒定,与假定(2)一致.

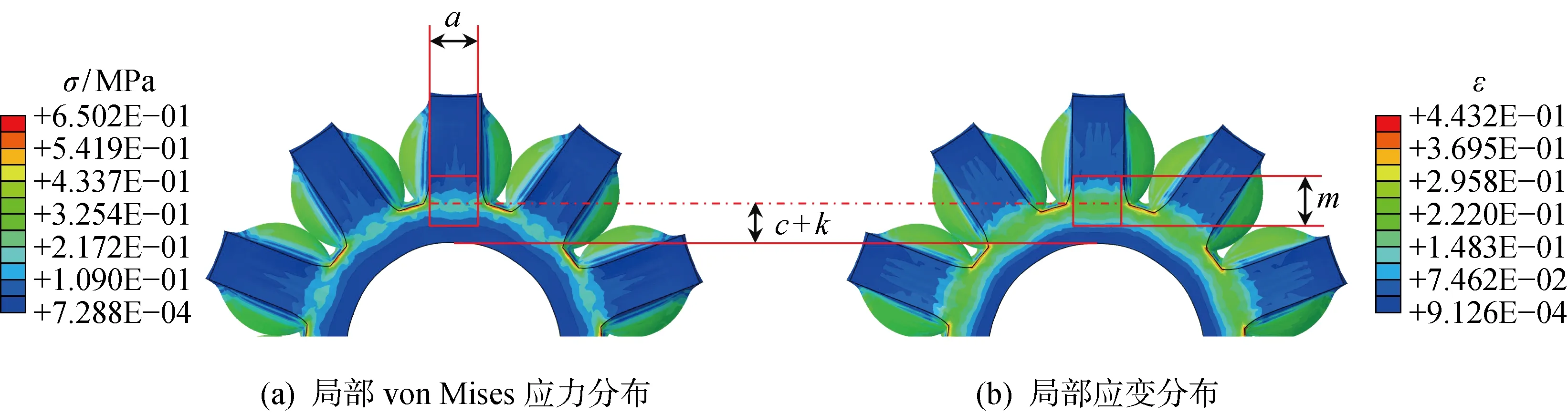
图8 p=35 kPa局部应力和应变Fig.8 Local stress and strain at p=35 kPa

4 固支-自由软体驱动器弯曲实验研究和结果分析

为了验证所提出的气动齿状软体驱动器简化力学模型的有效性和准确性,并测试不同气压作用下软体齿状驱动器的弯曲变形性能,对受不同气压载荷作用下的软体驱动器进行相应的实验研究,得到其弯曲变形构型.

4.1 实验平台的搭建

如图9所示,软体驱动器的左端面通过3D打印模具固定在实验平台上,以限制软体驱动器左端面的位移和转角;调节摄像机,使其镜头与桌面平行,垂直拍摄软体驱动器的变形;使用氩气为软体驱动器充气,手动缓慢调节气压值,待系统稳定后再读取气压值并拍摄软体驱动器的变形构型.

图9 实验平台示意图Fig.9 Experimental platform

4.2 实验结果

软体驱动器充气弯曲实验结果如图10所示.由图可见,对于固支-自由的软体驱动器,随着气压逐渐增大,软体驱动器的变形逐渐增大,即固有曲率轮廓逐渐增大,侧壁的膨胀程度也变大,底层的形状为圆弧形.测量驱动器上各个标记点的位置以获得实验数据.

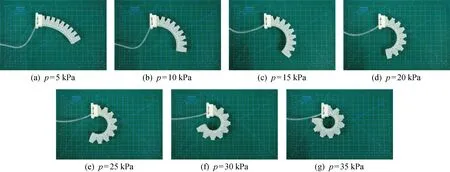
图10 实验变形结果Fig.10 Results of experimental deformation

4.3 实验验证与对比分析

模型编号及其对应的设置为:Model 1为考虑底层、侧壁、前后壁应变能的完整模型;Model 2为考虑底层、前后壁应变能的模型;Model 3为考虑底层、侧壁应变能的模型.

图11给出了驱动气压值p与软体驱动器弯曲角度α之间的关系.离散点的气压取值依次为p=5,10,15,20,25,30,35 kPa.由图可见,Model 1的结果与实验数据、Abaqus有限元仿真结果基本一致,其余模型的结果与实验数据均有误差,其中,当p<20 kPa时,Model 2的误差小于Model 3;当p>20 kPa时,Model 2的误差大于Model 3.

各个部分应变能的分布情况是影响不同模型精度的主要原因.图12给出了各部分应变能与驱动气压之间的关系.底层应变能与输入气压值呈线性正相关,并且在p<42 kPa的范围内,占主导作用.当p<20 kPa时,侧壁膨胀变形较小,侧壁应变能数值较小,Model 2的误差也较小,但此时前后壁比侧壁应变能大,Model 3的误差大于Model 2;当p>20 kPa 时,侧壁膨胀变形变大,应变能快速增大,Model 2的误差也增大.当p>42 kPa时,侧壁应变能大于底层应变能.前后壁的应变能与输入气压值呈线性正相关,但增长幅度较小,这是由于前后壁设计得比较厚(2 mm,是侧壁的两倍),主要起支承作用.前后壁变形主要是由底层弯曲和拉伸变形引起,如图12所示,前后壁和底层应变能的变化趋势一致,都随气压线性递增.此外,当p<30 kPa时,前后壁应变能大于侧壁应变能.

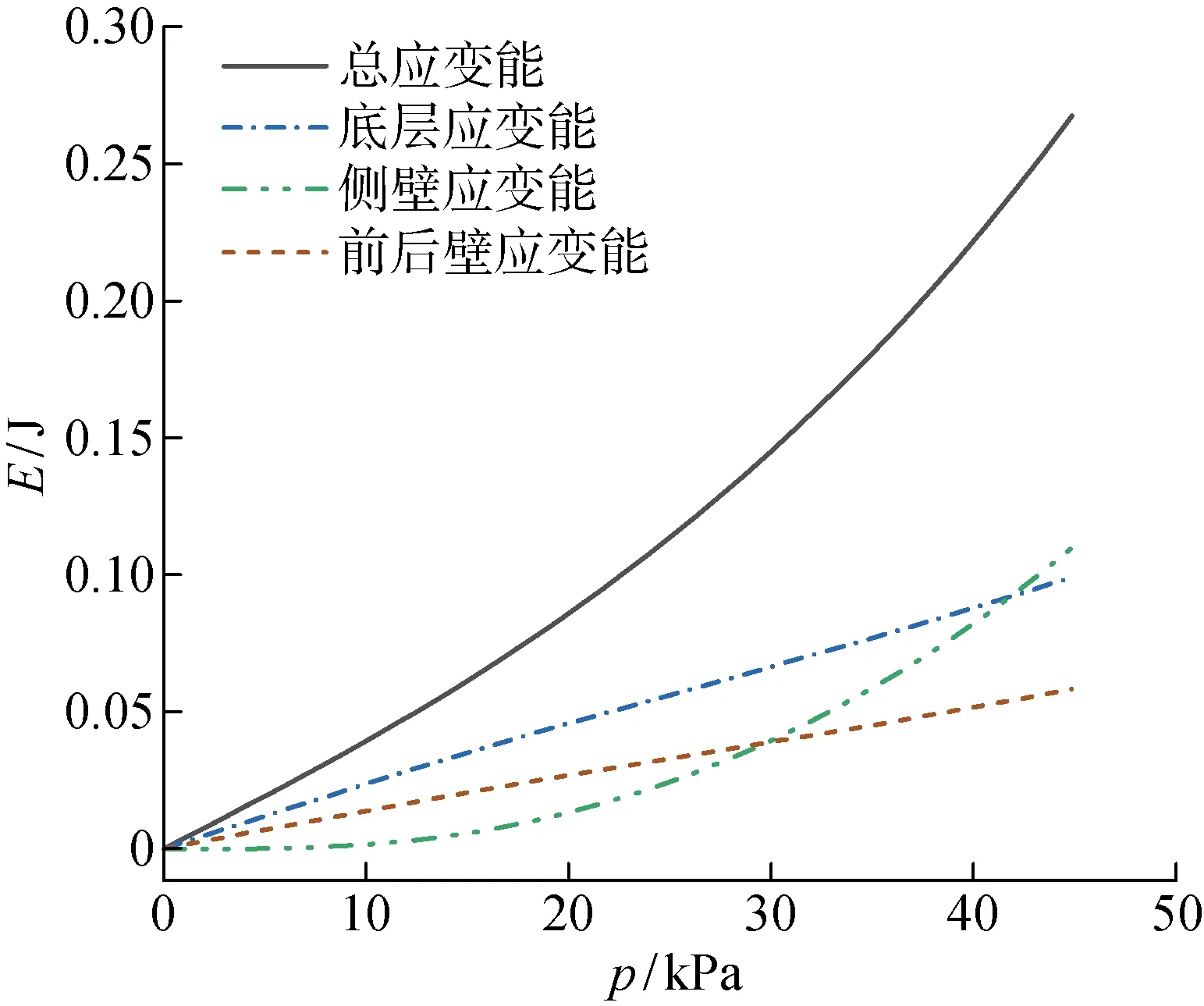
图12 应变能分布与气压值之间的关系曲线Fig.12 Strain energy distribution versus pressure

图13给出了气压分别为p=10,25 kPa时, Model 1至Model 3的变形构型与实验数据的对比,可以直观比对出Model 2和Model 3在两种情况下的误差大小,与图10的结果分析一致.

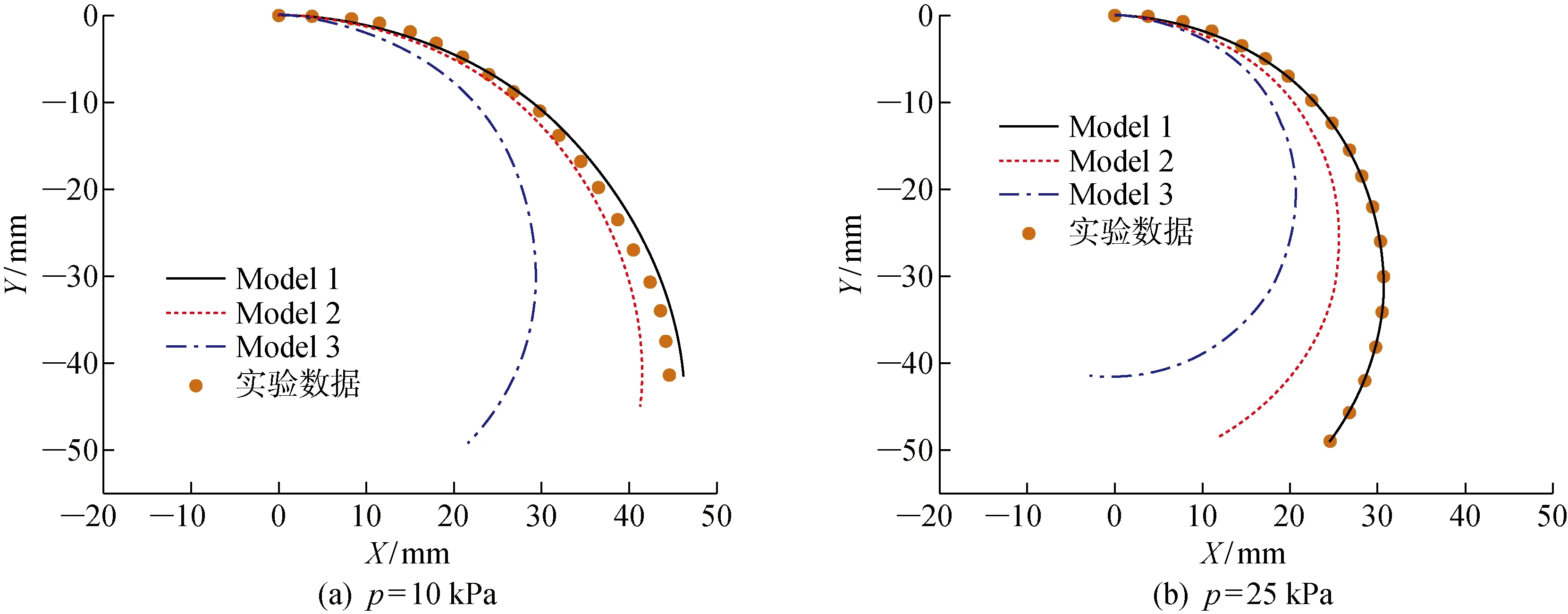
图13 不同模型弯曲构型与实验数据的对比Fig.13 Comparison of bending configurations of different models with experimental data

由上述分析可知,针对本文设计的气动软体驱动器的结构参数,只有同时考虑了底层、侧壁、前后壁应变能的完整模型Model 1与实验数据一致.其中,底层应变能在p<42 kPa的范围内占比最大,且当p>42 kPa仍占较大比例,不可忽略;前后壁应变能随着气压增大而线性增大,因此Model 3的误差整体成线性增大趋势;当p<20 kPa时,侧壁应变能可以忽略不计,因此Model 2在该范围内适用;当p>20 kPa时,必须考虑侧壁应变能的影响,因而Model 2的误差急剧上升.

图14为Model 1的变形构型与实验数据的对比,气压值依次为p=5,10,15,20,25,30,35 kPa.软体驱动器的变形随着气压增大而变大,当p<5 kPa 时,相邻两气腔并未完全充分接触,不满足本文提出的简化力学模型的假设条件,因此理论结果与实验数据不一致.对于其他气压值,理论结果与实验数据保持一致.

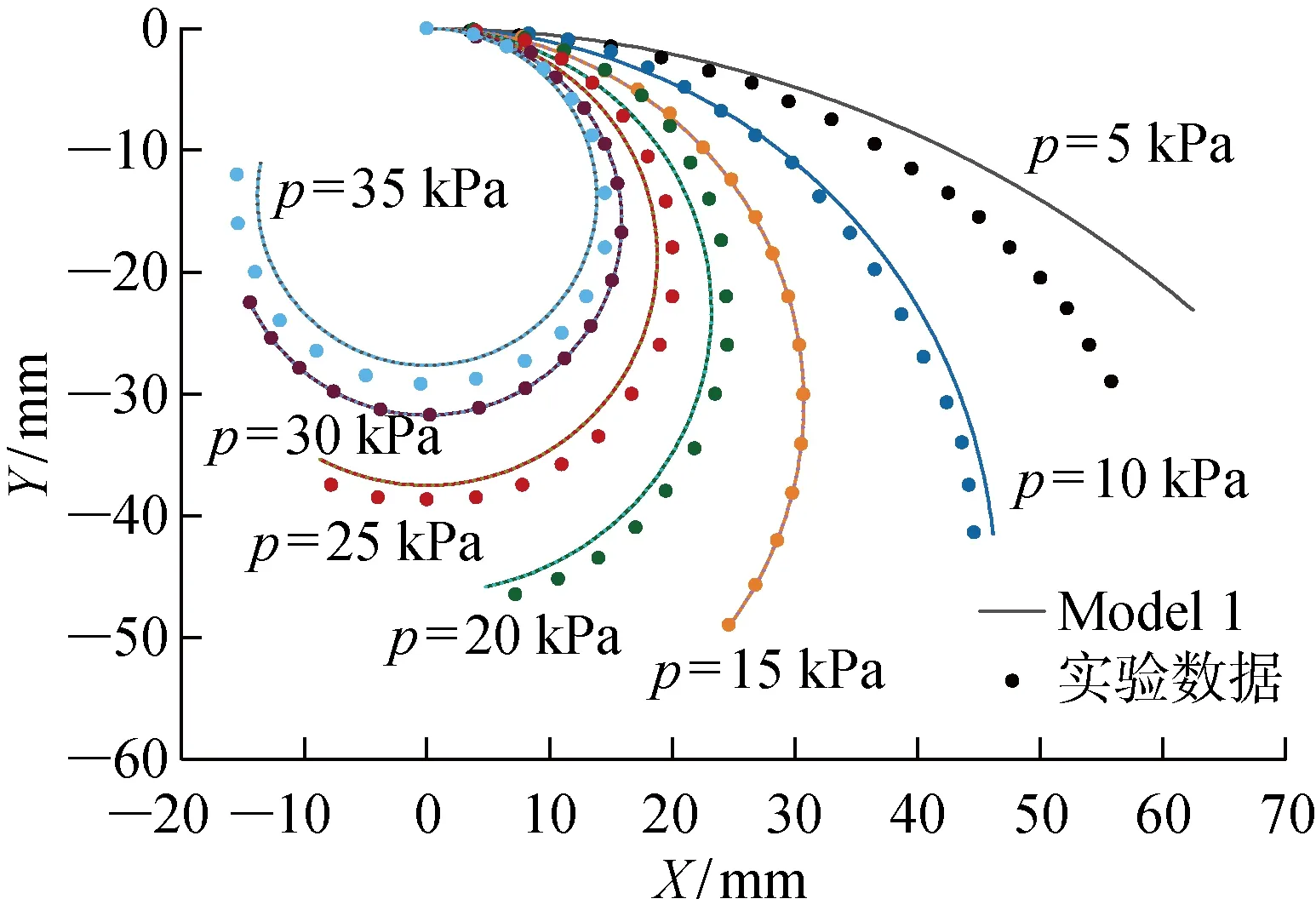
图14 Model 1与实验的构型对比Fig.14 Comparison of configurations obtained by Model 1 and experiment

驱动气压值与软体驱动器弯曲角度、腔室膨胀角之间的关系如图15所示.由图可知,驱动气压值p与软体驱动器弯曲角度α、腔室侧壁膨胀角θ之间均为线性正相关,有利于对软体驱动器进行调控,使其达到预设值,以满足操作要求.

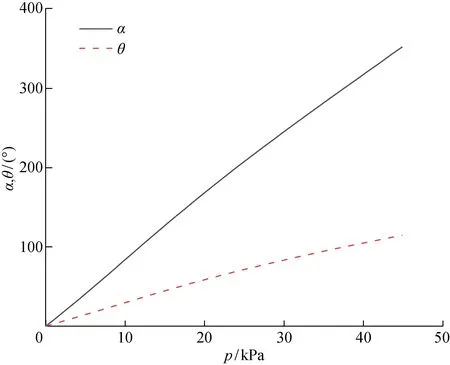
图15 Model 1的关系曲线Fig.15 Relationship curves obtained by Model 1

5 固支-末端受载荷作用的软体驱动器变曲率构型分析

在驱动器末端施加载荷F时,分别令气压值p=10,15,20 kPa.图16给出了在3组不同大小和方向的末端力F作用下,分段等曲率理论模型计算出的结果与Abaqus仿真结果的对比,括号中为Abaqus模拟出的不同气压作用下的驱动器末端坐标值,实线为Abaqus仿真结果,虚线为分段等曲率理论结果,两者基本一致,验证了分段等曲率模型的有效性.由于分段等曲率理论模型中存在一些假定,故其曲率比Abaqus模拟结果偏大.此外可以看出,在末端载荷作用下,驱动器整体构型为变曲率弧形,转角与气压呈线性正比关系只适用于局部气腔.

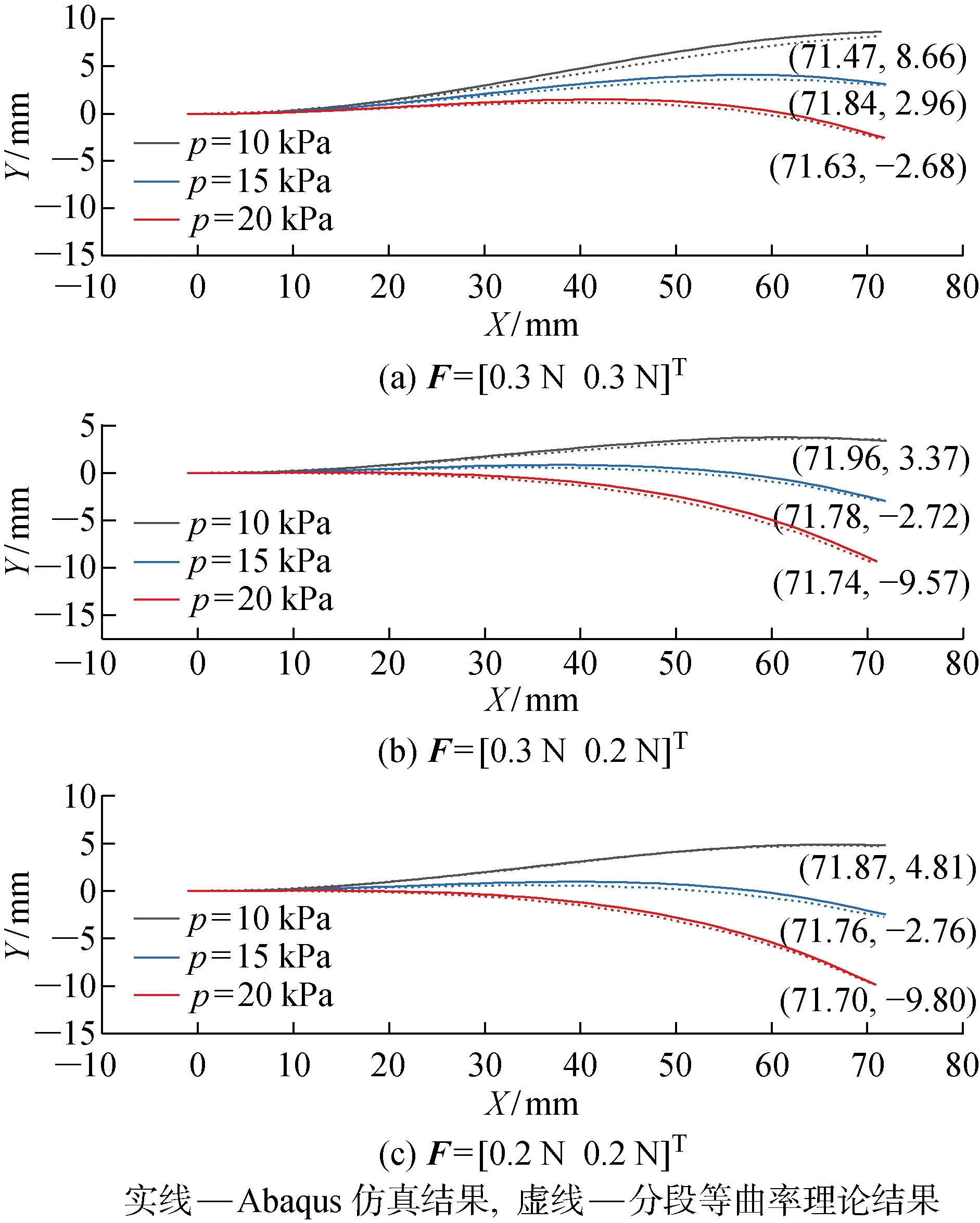
图16 固支-末端受载荷的软体驱动器变曲率底层构型Fig.16 Variable curvatures configuration of bottom surface of soft actuator at terminal load

从图16(a)和16(b)可以看出,取不同的竖直方向载荷对软体驱动器的构型影响较大,对于不同的气压值,竖直方向载荷为0.3 N时的驱动器末端Y坐标较0.2 N时大,底层变曲率现象更明显;对比图16(b)和16(c)发现,对于不同的气压值,水平方向载荷为0.3 N时的驱动器底层弧度较0.2 N时平缓,取不同的水平方向载荷对软体驱动器的构型影响较小,尤其是气压较大的情况.

6 结语

针对现有气动齿状软体驱动器的理论模型在模拟弯曲变形时精度较低的问题,提出一种综合底层、侧壁、前后壁应变能的理论建模方法.首先,假定软体驱动器的底层不可伸长,得到气腔侧壁膨胀变形后的角度θ与软体驱动器整体的弯曲角度α之间的几何关系,结合材料非线性,推导出底层和侧壁的应变能;其次,假定前后壁应变能在集中区域内关于对称轴线性分布,给出了前后壁应变能的表达式;最后,计算腔室体积的变化量,得到气压所做虚功,基于虚功原理建立了气动齿状软体驱动器的分段等曲率模型.根据建立的力学模型,可得驱动气压p和软体驱动器弯曲角度α之间的关系,该模型兼具精度和效率较高的优点,具有良好的适用性.

在理论建模的基础上,对该软体驱动器的变形构型进行了Abaqus仿真分析和实验研究.结果表明:对于固支-自由的软体驱动器,本文提出的完整模型Model 1在腔室侧壁充分接触(驱动气压p>5 kPa)时,与Abaqus仿真结果和实验数据基本吻合,验证了理论模型的准确性.对应变能分布进行分析表明:随着气压的增大,底层应变能和前后壁应变能线性增大,不可忽略;当p<20 kPa时,侧壁应变能很小,忽略侧壁应变能的Model 2仍具有较好的适用性,而忽略前后壁应变能的Model 3的误差较大,适用性较差.当p>20 kPa时,侧壁应变能随着气压快速增大,Model 2和Model 3均不能适用.对于固支-末端受力的软体驱动器,分段等曲率模型可以得到底层的变曲率构型.当同时受驱动气压p和末端载荷F作用时,由分段等曲率模型计算得到的3组算例的变形构型与Abaqus结果基本一致,验证了分段等曲率模型的有效性.研究发现,驱动器整体构型为变曲率弧形,转角与气压成线性正比关系只适用于局部气腔.

本文建立的气动齿状软体驱动器的分段等曲率模型,可为同类软体驱动器的运动分析提供理论指导.此外,相比于绝对节点坐标法,所建立的理论模型位形坐标数少,计算效率高,可有效降低对同类软体驱动器的计算仿真、优化设计和运动控制的时间成本.