未硫化橡胶黏弹塑性本构模型及有限元实现

王银龙, 李 钊, 李子然, 汪 洋

(1. 中国科学技术大学 近代力学系,合肥 230027; 2. 中国科学技术大学 中国科学院材料力学行为和设计重点实验室,合肥 230027; 3. 武汉第二船舶设计研究所, 武汉 430205)

橡胶制品的生产工艺一般包括原料混炼、半成品部件挤出/压延、成型、硫化定型4个过程.硫化定型工艺中,橡胶内部高分子链与硫原子之间发生化学反应,形成硫化交联网络,橡胶的弹性水平提高,黏塑性降低,耐老化性能增强[1],因此硫化橡胶得到较为广泛的应用,对其力学性能的研究也受到广大学者的重视.相比于硫化橡胶,未硫化橡胶对产品性能的影响却常被忽视,目前对其力学行为的研究依然较少.然而,未硫化橡胶的力学性能在很大程度上决定了前期的挤出、压延及成型工艺效果.事实上,上述过程中工艺参数如果不能与未硫化橡胶性能相匹配,往往会严重降低产品最终使用性能,甚至导致生产缺陷[2-3].近年来,随着各国对橡胶工业制造工艺研究的愈加深入,未硫化橡胶的力学性能也受到越来越多的关注.

文献[4-5]中最早较为系统地测试了未硫化炭黑填充橡胶在常温环境中不同变形模式(拉伸、压缩、剪切)下的非线性力学行为.结果表明,未硫化橡胶的力学响应具有明显的应变率相关性,以及迟滞效应、Mullins损伤、残余变形等非线性黏弹塑性特征.根据实验结果,文献[4-5]中提出一个基于Yeoh模型和广义Maxwell模型的非线性黏弹性本构模型,但此模型无法较好刻画未硫化橡胶应变率相关的塑性力学行为以及损伤软化等变形特征.为了改善表征效果,文献[6-8]中基于微球模型(Micro-sphere Model)提出一个新的内变量型黏塑性本构模型,此模型采用微球模型运动学框架对非弹性响应进行描述,无需对变形梯度进行乘法分解,但其表征效果并未得到明显提升.随后,上述研究基于黏弹性分数Zener模型[8]对未硫化橡胶的力学行为进行表征,该模型可以较好反映材料的弹性水平,但对黏塑性的表征效果仍较差.文献[9-11]中将1个 Marlow 弹簧模型和3个Maxwell模型并联,获得了未硫化橡胶Prony级数形式的黏弹性本构模型.此模型与Kaliske等[4]的本构模型并无本质区别,模型对未硫化橡胶单一工况下的松弛实验取得了较好的表征效果,尚无法表征未硫化橡胶复杂变形下的非线性黏弹塑性力学行为.需要说明的是,以上研究获得的本构模型虽然都包含应变率效应,但在本构模型参数拟合过程中均未同时包含多种应变率工况,本构模型能否较好地描述未硫化橡胶不同应变率下的非线性黏弹塑性响应仍需进一步验证.Kim等[12]通过多种拉伸实验探究未硫化橡胶应变率相关的非线性拉伸力学行为,并采用一个基于广义Maxwell模型和修正Kelvin模型的黏弹-黏塑性本构模型对其非线性力学行为进行表征,但该模型在较高应变率下(0.1 s-1)的表征效果略差,也未能较好反映出未硫化橡胶应变率相关的塑性变形特征.文献[13-14]中对未硫化橡胶开展不同应变率和不同温度下的拉伸实验,并基于八链模型和Bergström-Boyce流动法则提出了等温黏弹塑性本构模型和温度相关的黏弹塑性本构模型,较好地表征了未硫化橡胶较为复杂的非线性力学行为特征,如应变率效应、迟滞效应、残余变形等.值得一提的是,上述表征未硫化橡胶力学性能的本构模型[4-14]形式都较为复杂,参数众多,只有文献[6,12]中对提出的基于微球的本构模型给出了具体有限元实现过程,并进行了必要的数值验证,而其他本构模型能否用于未硫化橡胶复杂变形条件下的数值仿真仍有待研究.

本文对未硫化橡胶开展了不同应变率下的单调拉伸及循环拉伸加卸载实验,获得了未硫化橡胶较为复杂的非线性黏弹塑性力学行为.根据实验结果,提出了一个三网络黏弹塑性本构模型(TN模型)对未硫化橡胶的力学行为进行表征,模型充分考虑了胶料的超弹应力响应、非线性黏塑性流动、Mullins损伤软化等力学特征,能够较好表征未硫化橡胶非线性的黏弹塑性拉伸力学行为.最后,依托Abaqus有限元仿真软件用户材料子程序接口(UMAT),完成了上述TN模型的有限元实现,并对未硫化橡胶多步松弛加卸载和轮胎胎面胶压入模具的过程进行了有限元仿真,验证了TN模型的有效性和数值稳定性.

1 实验及结果讨论

1.1 实验材料及试件准备

实验采用的胶料均来自安徽佳通轮胎有限公司,为避免试件制备过程中橡胶内部发生硫化反应,胶料均为不含硫化体系的母炼胶.

实验试件采用哑铃状,具体尺寸如图1(a)所示.未硫化橡胶首先经过反复开炼,再置于平板硫化机的高温高压环境下获得厚度为2 mm的橡胶板,最后通过裁切获得哑铃状试件.实验过程中采用自动网格法[15-16]记录试件全场的应变信息,实验前需在试件表面制作网格点阵,如图1(b)所示.更为具体的试件制备方法以及网格点阵制备方式已在此前的研究[13]中发表,在此不再赘述.

1.2 橡胶实验及结果分析

单调拉伸工况下未硫化橡胶的拉伸实验结果如图2(a)所示.图中:εeng为工程应变;σeng为工程应力.从图中可以看出,不同应变率下未硫化橡胶具有相似的非线性力学特征,在拉伸初始时具有很小的线性段,随后发生软化行为,最终应力趋于平缓.胶料拉伸应力水平表现出明显的应变率相关性,随着应变率增加,初始刚度显著增加,应力水平提高.相比于硫化橡胶,未硫化橡胶在100%的应变范围内未出现反“S”现象,可能由其内部未形成交联网络所致.

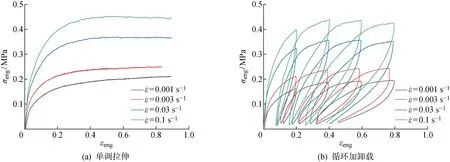
图2 未硫化橡胶不同应变率下拉伸实验结果Fig.2 Mechanical behaviors of uncured rubber at different strain rates

循环拉伸加卸载实验中,未硫化橡胶同样表现出明显的应变率相关性,且在加载段的应变率相关性略大于卸载段的应变率相关性,如图2(b)所示.此外,还可以看出,未硫化橡胶存在较为明显的Mullins软化现象,以及显著的迟滞效应和残余变形.Mullins软化效应反映了试件在首次拉伸时的损伤,为了更清晰地观察未硫化橡胶的软化现象,图3给出了其在不同应变率下随拉伸循环次数(C)增加,拉伸上升段在前20%应变范围内的切变模量(G).可见,随着循环次数增加,胶料切变模量明显降低,且在较高应变率时降低速度更快.迟滞效应反映了循环加卸载实验中的能量耗散,未硫化橡胶迟滞效应同样受到应变率的影响,随着应变率增加,迟滞效应有所增强.由于未硫化橡胶黏塑性较强,每次卸载后均存在一定的塑性残余变形,且残余变形量随着循环次数的增加而累计增加,随着应变率的增加有所降低.

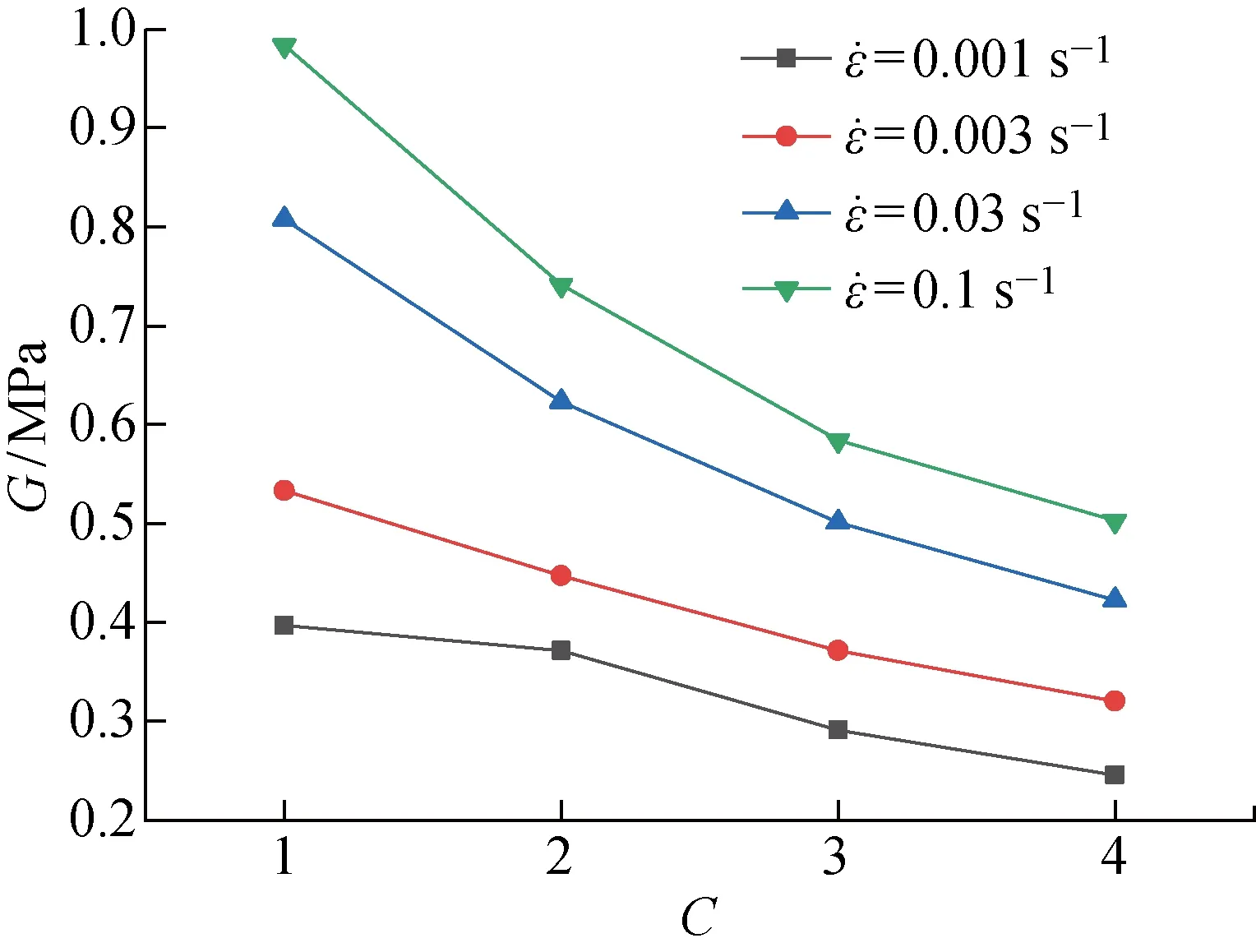
图3 不同应变率下4次上升段切变模量Fig.3 Shear modulus in four loading steps at different strain rates

2 未硫化橡胶黏弹塑性本构模型

基于对未硫化橡胶实验结果的分析,提出了TN模型对未硫化橡胶的力学行为进行表征,模型的黏塑性响应基于对变形梯度的乘法分解,具体推导过程介绍如下.

2.1 变形梯度分解

对于不可压缩材料,变形梯度F通过乘法分解为形变分量(Distortional Part)与体积分量(Dilatational Part)[17]:

F=FdisFdil

(1)

形变分量与体积分量分别具有以下形式[18]:

(2)

式中:J为变形梯度的行列式;I为单位张量;det(Fdis)=1.

此时左Cauchy-Green变形张量可表示为

B=FFT=J2/3B*

(3)

(4)

式中:B*为B的形变分量.

对于近似不可压缩橡胶类材料黏塑性变形,形变分量也可分解为弹性变形分量和黏塑性分量[19]:

Fdis=FeFv

(5)

式中:Fe为变形梯度的弹性分量;Fv为变形梯度的黏塑性分量.

此时可获得速度梯度Ldis:

(6)

(7)

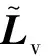
(8)

2.2 TN模型

本文提出的TN模型包含3个并联网络,如图4所示.其中一个网络(网络A)为超弹性网络,用于表征未硫化橡胶的超弹性应力响应;另外两个网络为黏塑性网络(网络B、C),用于表征其黏塑性响应.不同于通常所采用的广义Maxwell模型,黏塑性网络B、C采用了基于高分子链微观运动学机制的Bergström-Boyce流动模型,能更好地表征未硫化橡胶的非线性黏塑性流动特征.同时,模型引入了基于分子链运动演化机制的损伤模型来表征未硫化橡胶的Mullins损伤软化效应.

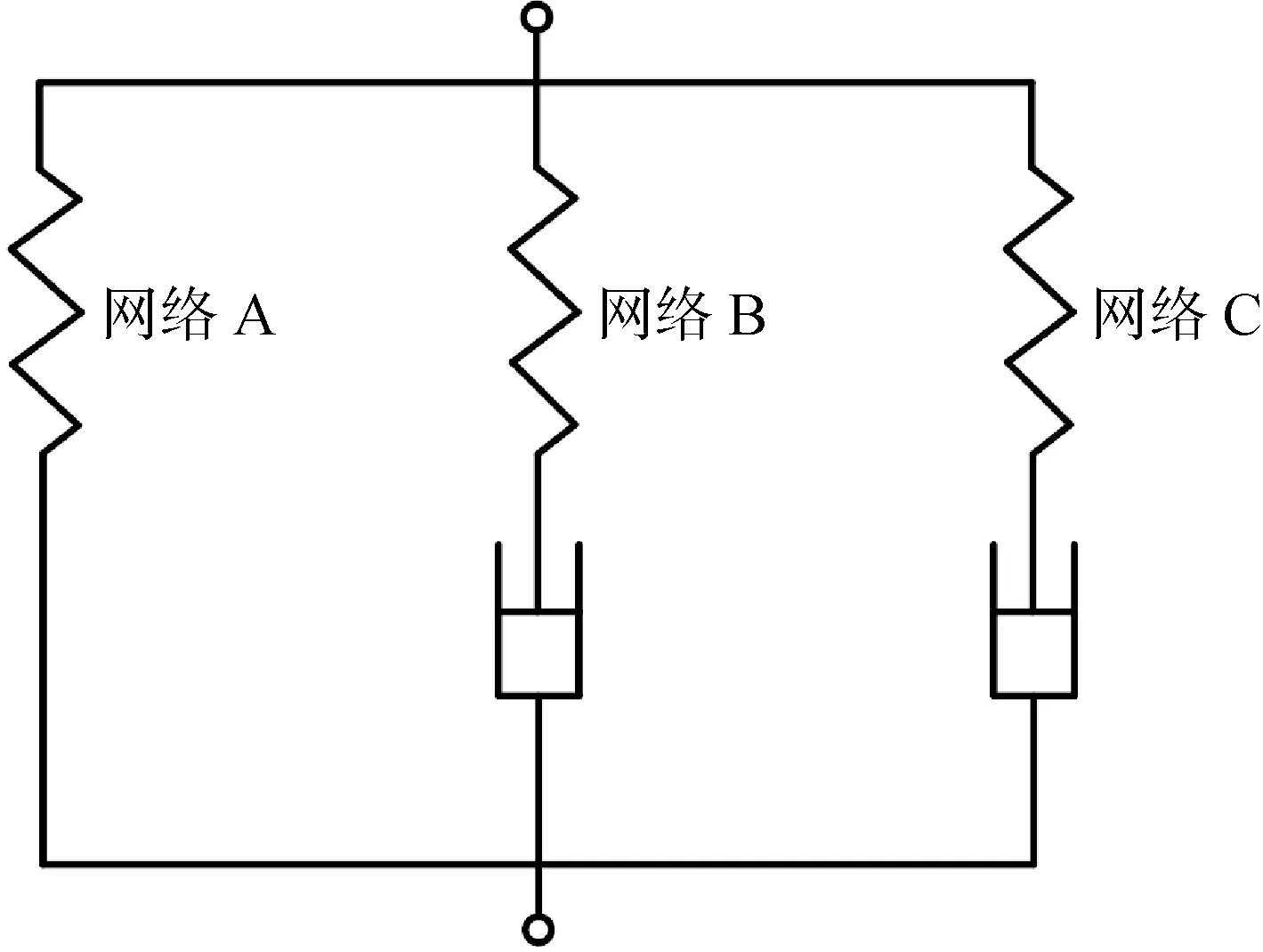
图4 TN模型框架Fig.4 Frame of TN model

模型Cauchy应力σtol为3个网络Cauchy应力的和:

σtol=σA+σB+σC

(9)

2.2.1TN模型应力响应 橡胶类材料的本构行为常通过应变能密度函数进行表征[1, 21],目前针对橡胶类高分子材料已经发展出多种不同形式的应变能密度函数,包括唯象应变能密度函数和基于分子网络的应变能密度函数[22-24].其中,Arruda等[25]基于非高斯链分子网络所提出的八链模型参数简单,表征效果优异,应用较为广泛.考虑到未硫化橡胶具有相似的分子网络构型,在此采用八链模型应变能密度函数来表征未硫化橡胶的超弹应力响应,应变能密度表达式为

(10)

(11)

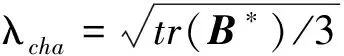
对于超弹性力学响应,Cauchy应力可用应变能密度函数[18]表示为

(12)

式中:C为右Cauchy-Green变形张量.将应变能密度函数表达式(10)和(11)代入上式,并将C以不变量的形式写入,即可获得八链模型的Cauchy应力表达式[25]:

K(J-1)I

(13)

对于本文中三网络框架,3个网络的Cauchy应力可通过八链模型分别表示为

K(J-1)I

(14)

K(J-1)I

(15)

K(J-1)I

(16)

超弹性网络(网络A)的Cauchy应力由整体变形梯度决定;黏塑性网络(网络B、C)的变形梯度可进行乘法分解为弹性分量和黏塑性分量:F=FeBFvB,F=FeCFvC,其Cauchy应力仅由弹性分量提供,即

(17)

(18)

式中:FeB和FeC分别为B、C网络的弹性变形梯度;FvB和FvC为B、C网络的黏塑性变形梯度.

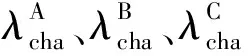
(19)

(20)

(21)

2.2.2黏塑性流动模型 要获得黏塑性网络B、C的弹性变形梯度,首先需要求解其黏塑性变形梯度,故需要合适的模型来对黏塑性流动进行表征.由1.2节实验结果可知,未硫化橡胶力学行为较为复杂,通常的Maxwell模型不足以较好地表征其非线性黏塑性,故本文采用了基于高分子链微观动力学机制的Bergström-Boyce流动模型.该流动模型认为橡胶类聚合物材料的黏塑性变形是分子链的布朗运动(Brownian Motion)和“爬行”运动(Reptation Motion)联合作用的结果[18],基于此假设,模型具有以下的表达形式:

(22)

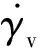
(23)

(24)

将式(22)和(23)代入黏塑性变形速度梯度表达式(8),即可获得黏塑性变形梯度的时间导数:

(25)

网络B、C中黏塑性变形梯度的时间导数分别为

(26)

(27)

对式(26)和(27)进行时间积分即可获得B、C网络的黏塑性变形梯度.

2.2.3Mullins损伤效应 此TN模型从橡胶高分子链的分子演化理论[26-27]出发来考虑未硫化橡胶的Mullins软化效应.对于颗粒填充聚合物材料,填充颗粒和高分子链之间的联接包括强化学联接(共价键)及弱物理联接[28].在拉伸过程中,物理联接(填充颗粒与高分子链之间),以及部分化学联接(高分子链之间或填充颗粒与高分子链之间)达到极限伸长而发生断裂,引起软化现象.对于未硫化炭黑填充橡胶,物理联接的强度远远小于化学共价键联接,故可认为拉伸过程中发生断裂的化学共价键数量相对于物理联接点很少,可以忽略不计[27].

TN模型中,A网络代表了由物理联接构成的炭黑颗粒填充高分子链网络,用于表征未硫化橡胶的超弹性响应,而B、C黏塑性网络代表了由化学共价键联接构成的自由分子链网络,用于表征未硫化橡胶的黏塑性响应.Mullins损伤主要来自于A网络中填充颗粒与高分子链之间物理联接的破坏,该破坏一方面减少了填充颗粒与高分子链之间的联接点数目,引起分子网络中N的增加,另一方面导致n减少[26].物理联接的破坏程度与λcha有关,故n的减少由λcha决定,其变化情况可用A网络中切变模量GA=nAkBT的整体变化来表示[27]:

(28)

N的变化同样与λcha有关:

(29)

式中:C4～C9均为材料常数.

将式(28)和(29)代入Cauchy应力表达式(14),可得包含应力软化效应的炭黑填充分子链网络的Cauchy应力表达式:

dev(B*)+K(J-1)I

(30)

化学共价键联接构成的自由链网络(网络B、C)对Mullins效应的影响主要来自于分子链的运动演化回复,并表现为胶料模量的增大.在此采用微观泡沫模型(MFM)[29]的形式来计及分子链运动的影响,并将原模型中的缩减密度改写为应力回复因子R(取值应大于1,本文取为1.2)以体现分子链的运动回复对应力的增强效果,从而获得了切变模量与体积模量的表达式:

(31)

(32)

式中:G0、K0为网络初始切变模量和体积模量,G0=nkBT;α和h为模量缩放因子.

将式(31)和(32)代入Cauchy应力表达式(15)和(16),可获得包含分子运动演化效应的B、C网络Cauchy应力表达式:

(33)

(34)

式中:G0B、G0C和K0B、K0C分别为B、C网络的初始切变模量和体积模量.

2.3 本构模型表征效果

曲线拟合即实验曲线与表征曲线之间误差最小化的过程,本文采用最小二乘法进行误差计算:

(35)

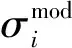
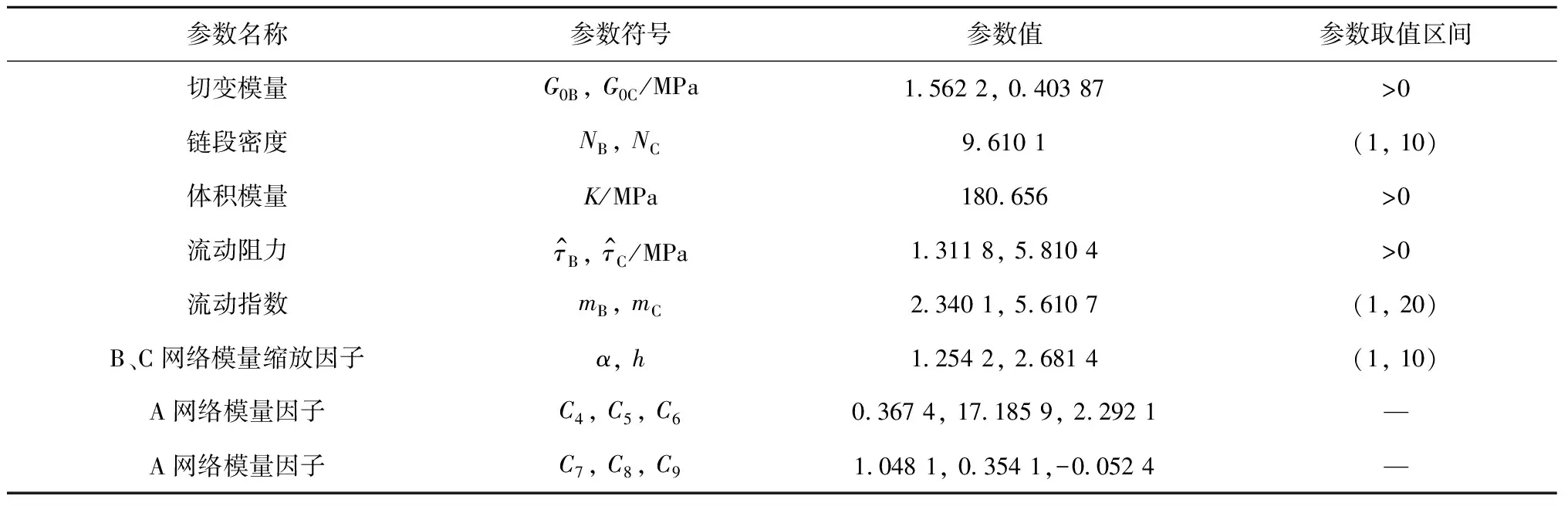
表1 三网络模型拟合参数Tab.1 Ultimate optimization parameters of NT model

模型参数拟合过程采用梯度下降法,拟合结果如图5所示.图中:εtrue为真应变;σtrue为真应力.可以看出,不同应变率下的拟合曲线与实验曲线吻合良 好, 未硫化橡胶的复杂力学行为特征, 包括迟滞效应、残余变形及软化现象均得到了较好的表征.4种不同应变率下的表征结果在同一套拟合参数下完成,拟合参数如表1所示.

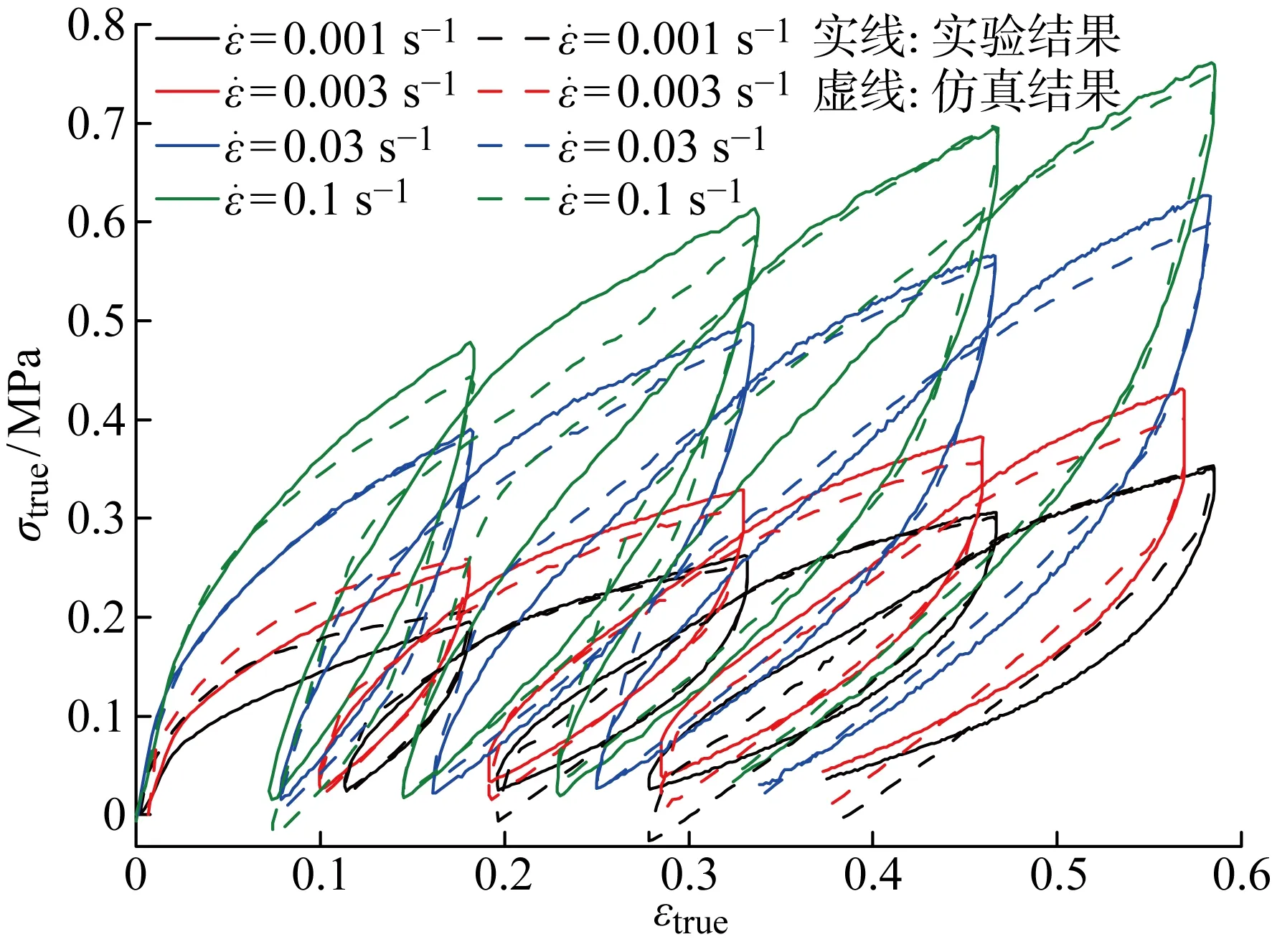
图5 TN模型表征结果Fig.5 Fitting result using TN model

3 TN模型的有限元实现及验证

获得的本构模型若要应用于工程实践,则需要将其进行数值实现.本文依托于有限元软件Abaqus,完成了TN模型用户材料子程序(UMAT)的开发,并进行了仿真计算以验证模型的有效性和数值稳定性.

模型有限元实现过程中采用的应力更新算法为二阶精度的显式龙格库塔算法(Explicit Midpoint Rule)[32],该算法流程清晰,灵活性强,能够较好地平衡计算精度、数值稳定性以及易数值植入性.采用t代表前一个增量步,t+1代表后一个增量步,则该应力更新算法步骤如下.

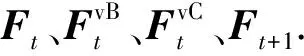
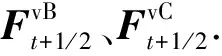
(3) 对t时刻和t+1时刻总变形梯度平均获得t+1/2时刻总变形梯度Ft+1/2.

(6) 检验B、C网络的黏塑性变形梯度是否满足误差准则,若满足则进入第(7)步,否则更新时间步长后返回第(2)步.

(7) 计算t+1时刻B、C网络的弹性变形梯度并根据式(14)～(16)计算t+1时刻Cauchy应力.

(8) 储存自定义状态变量并计算一致切线刚度矩阵(Jacobian矩阵).

获得TN模型用户材料子程序后,为验证其有效性,首先采用此子程序对一个单元在不同工况下(拉伸、压缩、剪切)的力学行为进行了数值计算,各工况下单元的Mises应力(S)分布情况如图6所示.图7给出了在不同应变率下拉伸工况的仿真结果与测试结果的对比情况.可以看出,仿真结果能准确再现不同应变率下的拉伸应力应变曲线.

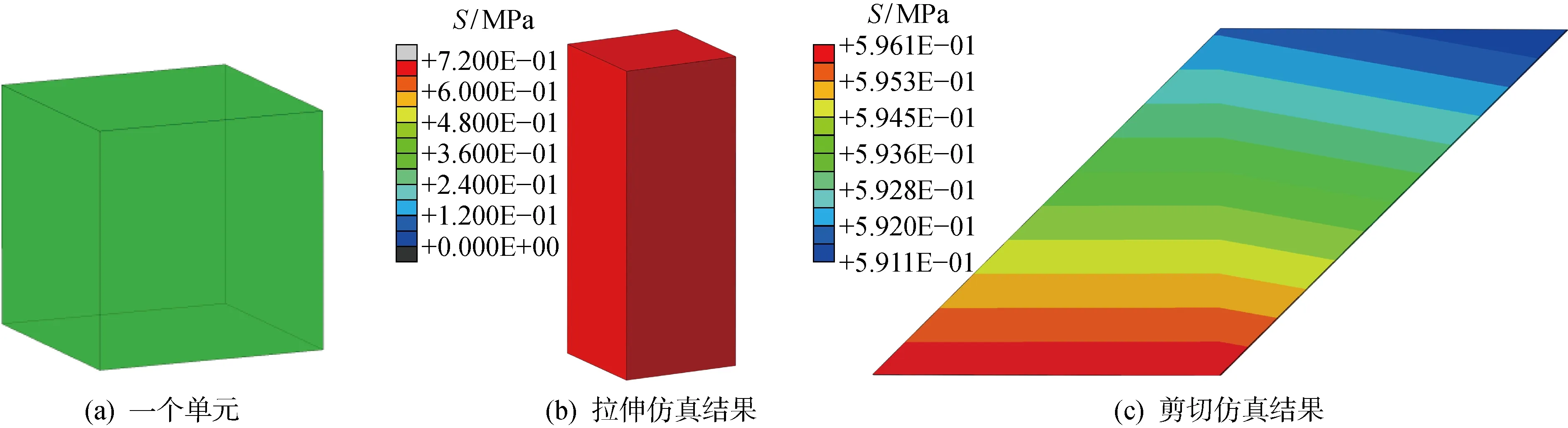
图6 一个单元的仿真结果Fig.6 Simulation results of a single element

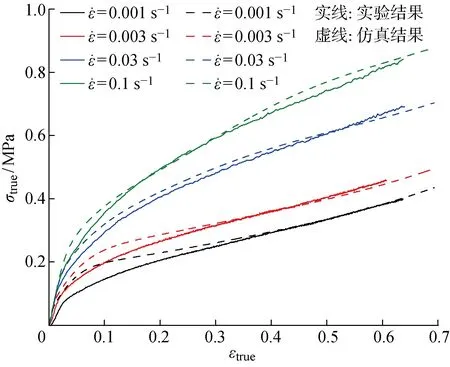
图7 拉伸仿真结果与单调拉伸实验结果对比Fig.7 Comparison of simulation results with experiments under uniaxial tensile conditions

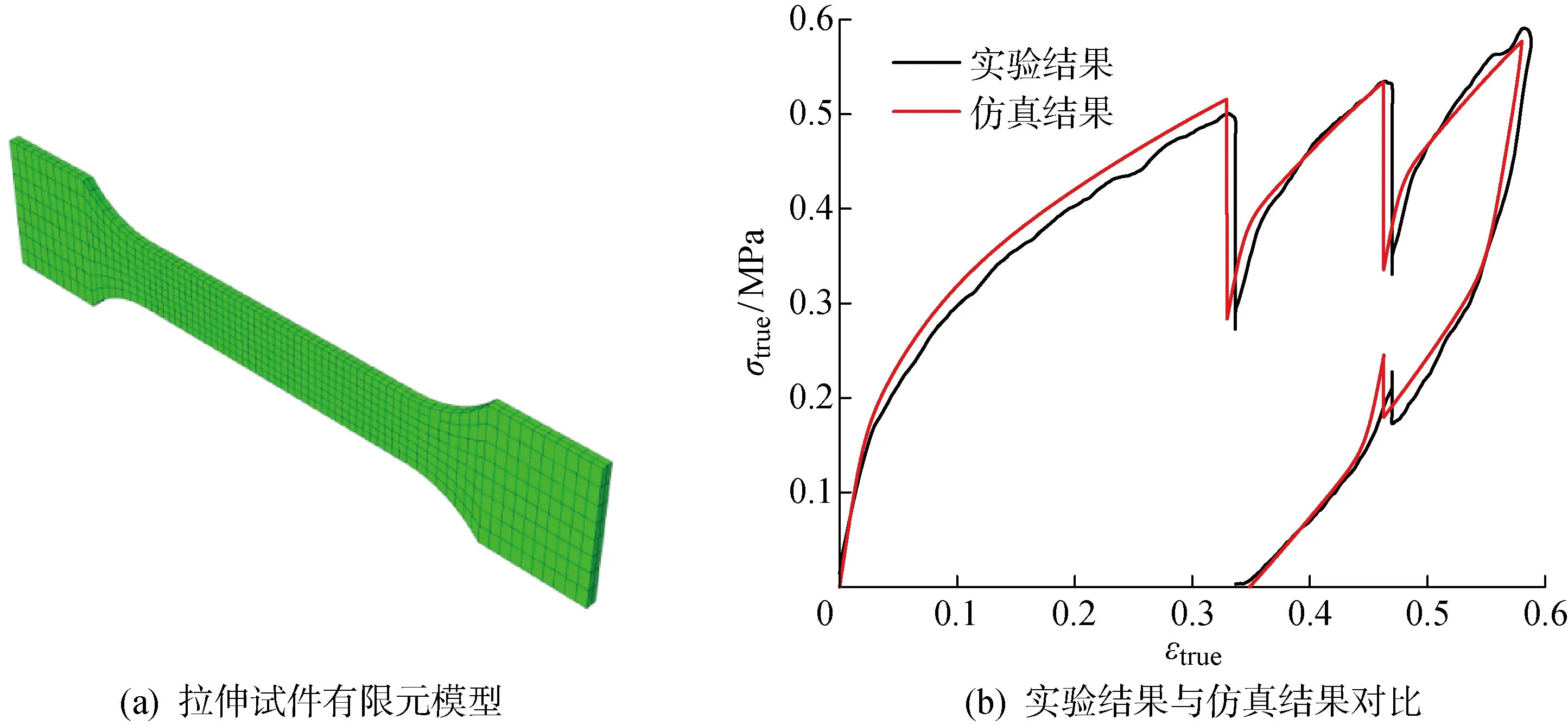
图8 多段松弛加卸载实验与仿真结果对比Fig.8 Comparison of multistep tensile relaxation test and simulation result

另一方面,未硫化橡胶多用于成型工艺,此过程中胶料需经历较为复杂的变形,故本构模型在复杂变形工况下的计算稳定性尤为重要.为了验证TN模型的数值稳定性,对轮胎胎面胶压入模具的成型过程进行了数值仿真,如图9所示.此模型实际上是对轮胎胎面胶纵向花纹沟成型工艺的简化,如图9(a)所示,模型轴对称分布,且仅包含一条花纹沟.采用轴对称有限元模型对此过程进行仿真,如图9(b)所示,将胎面胶分为5层以便于观察胶料流动,总厚度为20 mm,宽度为80 mm,采用的单元类型为CAX4H,节点数为 2 721 个,单元数为 2 594 个.模具采用离散刚体,深度为15 mm,中间的拱形突起高8.75 mm,宽7.5 mm.对胎面胶上层节点施加径向向下的位移边界条件,速度为0.5 mm/s,橡胶与模具之间的接触摩擦因数设为0.5.胎面胶压入模具后的各层胶料分布如图9(c)所示,由于未硫化橡胶具有近似不可压缩性,胶料充满模具后由两侧溢出.图9(d)和9(e)给出了此时刻胎面胶的应力和应变分布情况,可以看出,中间的拱形突起处胶料流动较为剧烈,存在一定的应力应变集中,靠近模具边缘处的应力应变分布高于底部平坦部位.胶料流动情况以及应力应变分布情况与文献[6, 8]中实验及仿真结果基本一致.综上可见,TN模型在复杂变形工况下仍能给出合理的计算结果,表明TN模型具有良好的数值稳定性.

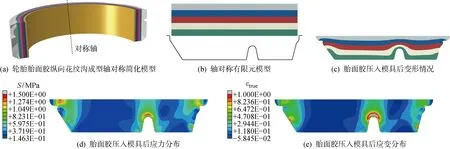
图9 胎面胶压入模具过程仿真Fig.9 Simplified molding process of a tire tread

4 结论

(2) 根据实验结果,提出一个用于表征未硫化橡胶黏弹塑性力学行为的TN本构模型,模型由一个超弹性网络和两个非线性黏塑性网络构成.3个网络的应力响应均基于超弹八链模型,同时在黏塑性网络中采用了Bergström-Boyce流动法则描述胶料的非线性黏塑性流动.此外,模型从橡胶高分子链的分子演化理论出发考虑了未硫化橡胶的 Mullins 损伤软化效应.采用TN模型对未硫化橡胶循环拉伸加卸载实验曲线进行表征,表征结果与实验结果吻合良好,胶料的各种拉伸力学特征均得到了较好的体现.

(3) 依托有限元仿真软件Abaqus,完成了TN模型用户材料子程序(UMAT)的开发,并对试件单调拉伸和多段松弛拉伸加卸载实验进行了仿真,仿真结果与实验结果吻合较好,验证了此TN模型的有效性.最后,采用TN模型对轮胎胎面胶压入模具的过程进行数值计算,进一步验证了模型在复杂变形工况下良好的数值稳定性.