一种CNN-LSTM船舶运动极值预报模型

詹 可, 朱仁传

(上海交通大学 船舶海洋与建筑工程学院;海洋工程国家重点实验室,上海 200240)

船舶在航行时受风、浪、流等复杂外力的作用,各自由度上均会产生不规则的摇荡运动.当摇荡幅度过大时,船舶的航行和作业安全将会受到严峻的挑战.提前预报船舶未来的摇荡运动可为操作人员提供更多的决策时间,提高安全性与稳定性.

船舶运动响应的短期预报可以视作一个典型的时间序列预测(Time Series Forecasting, TSF)问题.经典的时间序列分析方法,如自回归模型(Auto Regression Model, ARM)[1]、卡尔曼滤波(Kalman Filtering)[2]等结构简单,计算效率高,但在处理非平稳、非线性的时间序列时效果不佳.支持向量机(Support Vector Machines, SVM)、人工神经网络(Artificial Neural Network, ANN)等机器学习模型具有强大的非线性拟合能力,因而在船舶运动预报领域得到广泛重视.Zhou等[3]使用结合经验模态分解的最小二乘支持向量机(Least Squares Support Vector Machines, LS-SVM)预报船舶运动.Pena等[4]通过人工神经网络对船舶横摇运动进行预测.近年来,循环神经网络(Recurrent Neural Network, RNN)及其变种,尤其是长短时记忆(Long Short-Term Memory, LSTM)网络[5]成为了热门模型.RNN中隐藏层的输入包含了上一时刻隐藏层的输出,能够更好地记忆并学习序列的历史信息,因而更适用于长时间序列的预报,LSTM则在RNN的基础上引入了记忆状态和门控单元,进一步提升了预报效果.长短时记忆网络等还可与卷积神经网络(Convolutional Neural Networks,CNN)、注意力机制(Attention Mechanism)等相结合.Wang等[6]结合CNN与双向LSTM,建立了基于风速、舵角等多维输入的船舶横摇运动预报模型.Wang等[7]引入时间模式注意力机制(Temporal Pattern Attention, TPA)对双向LSTM输出结果进行修正,提升了横摇运动预报效果.Zhang等[8]将多尺度注意力机制与双向LSTM结合以预测船舶运动.除应用新的机器学习模型外,使用小波变换(Wavelet Transform)[8]、经验模态分解(Empirical Mode Decomposition, EMD)[9]等数据前处理方法也可提升预报精度.

船舶摇荡运动具有明显的周期性,且一般不会出现高频震荡,因而根据序列局部极值点的信息即能较好地还原船舶的运动时历.从实际需求出发,船舶航行与作业时也更加关注摇荡极值,而当前尚未对此做出深入的研究.本文结合船舶各自由度摇荡运动频谱捕获序列中的局部极值和周期信息,在此基础上构造CNN-LSTM深度学习模型,通过CNN的卷积运算进行序列特征提取,再输入LSTM模块进行进一步的时间特征学习,最终得到预报结果.对S175船进行仿真实验,结果表明,该模型预报效果优于LSTM、门控循环单元(Gated Recurrent Unit, GRU)等模型,具有较高的应用价值.

1 CNN-LSTM船舶运动极值预报模型

1.1 基于运动响应谱的特征信息提取

对于船舶单个自由度摇荡运动数据构成的一维时间序列X={xi,i=1, 2, …,N}∈R1×N,采样间隔为Δt,可采用滑动窗口的形式捕获其局部极值点,其计算流程如下式:

(1)

式中:C∈R1×N为判定向量,判定数据点是否为局部极值点,0表示非局部极值点,1表示为局部极值点;P∈R1×N为位置向量,记录局部极值点在原始序列中的位置;E∈R1×card(P)为极值点向量,记录局部极值点的数值,card(P)为P中的元素个数;T∈R1×card(P)为周期向量,记录相邻局部极值点的距离;d为滑动窗口宽度.

对于船舶摇荡运动序列,所取窗口宽度过小时容易受到噪声的干扰;所取窗口宽度过大时,又会造成信息损失.不同窗口宽度对极值信息提取的效果如图1所示.图中:X表示位移;t表示时间.

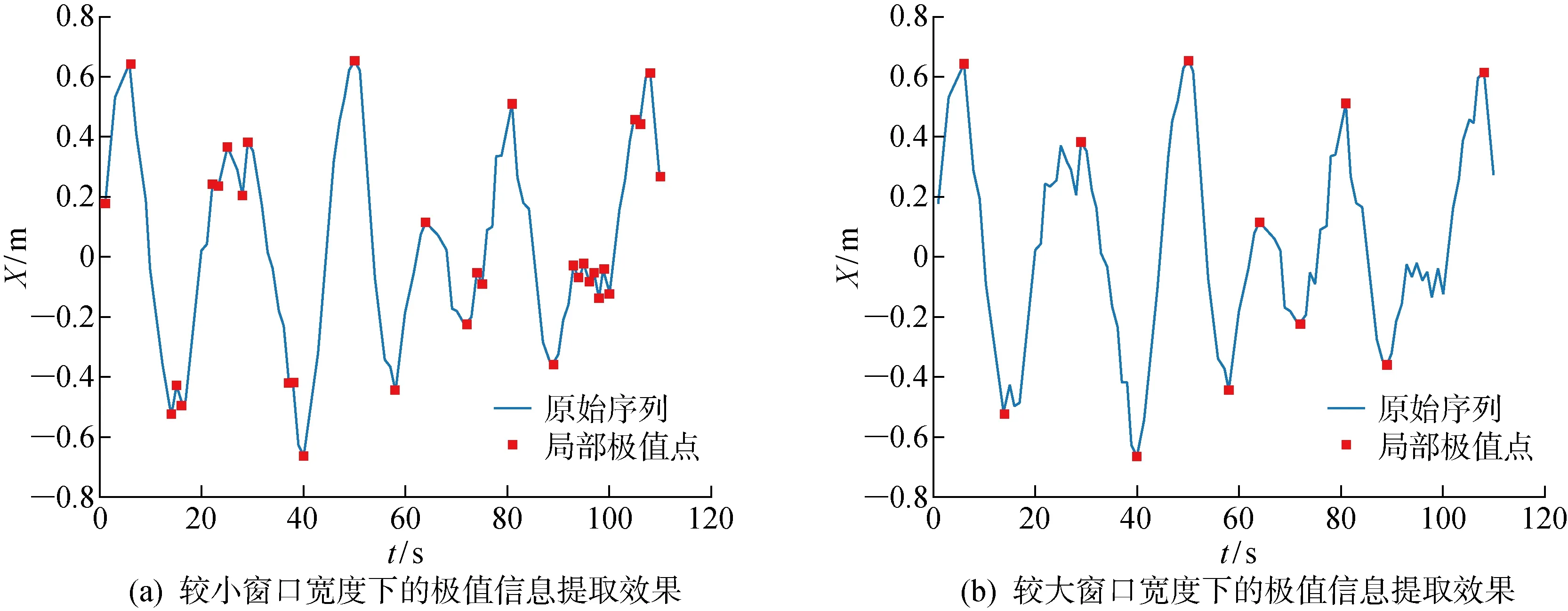
图1 不同窗口宽度对极值提取效果的影响Fig.1 Effect of different window widths on extreme value extraction

考虑到船舶运动频谱在较长的时间内保持相对稳定,且包含船舶运动的频域信息,本文选择结合运动响应谱来确定窗口宽度.各自由度的运动响应谱通过Welch法[10]计算,其基本步骤如下.

对于长度为N的序列X,将其分为L个小段,分别记作li(i=1, 2, …,L),每个小段长度为M,相邻小段间重叠长度为M/2,则段数

(2)

对每个小段添加窗函数w(m)后作傅里叶变换:

(3)

式中:i=1, 2, …,L;j为虚数单位;ω为频域中的对应频率.

窗函数一般取Hanning窗,其表达式为

(4)

式中:m=0, 1, …,M-1.

计算各小段功率谱的均值作为最终结果:

(5)

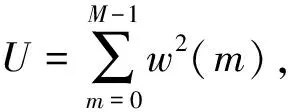
(6)

式中:[·]为取整函数.

1.2 卷积神经网络

卷积神经网络是一类以卷积运算为核心的深度前馈神经网络.完整的二维卷积神经网络通常包括输入层、卷积层、池化层、全连接层、输出层等模块[11].卷积神经网络对数据的特征提取主要依赖于卷积层中的卷积核,其计算过程[12]为

(7)

如图2所示,卷积核(也称为过滤器)通过逐步平移的方式扫描二维数据并进行卷积运算,从而提取数据特征,其中蓝色区域为卷积核计算区域,黄色部分为卷积核,橙色部分为卷积核计算结果.为充分提取特征信息,一般需要设置多个卷积核.

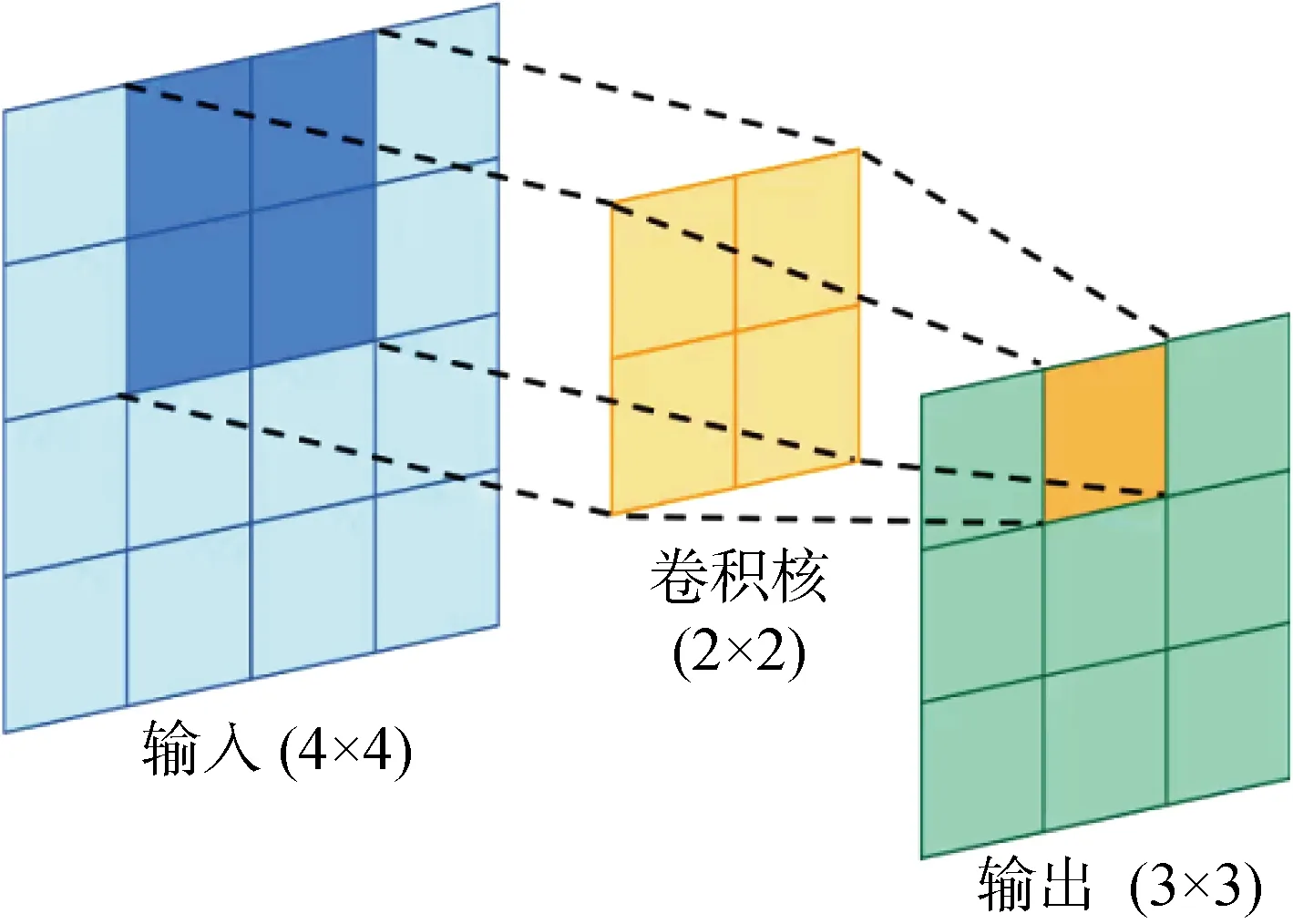
图2 卷积核计算过程Fig.2 Convolution kernel calculation process

池化层采用类似的逐步平移方式扫描卷积层输出的特征图,依次捕获过滤器内的最大值,从而缩减数据规模,降低模型复杂度.通过多个卷积层和池化层的交替堆叠,可以更好地提取数据的深层特征.

1.3 长短时记忆网络

长短时记忆网络是循环神经网络的一个变种,该网络能有效解决传统模型训练过程中的梯度消失问题[13],适用于长时间序列的分析和预测.与标准的RNN网络相比,LSTM在隐藏层神经节点中增加了一个记忆状态单元来存储过去的信息,并用3种门控结构(输入门、遗忘门、输出门)来控制历史信息的遗忘与更新.LSTM隐藏层神经元的基本结构[14]如图3所示.

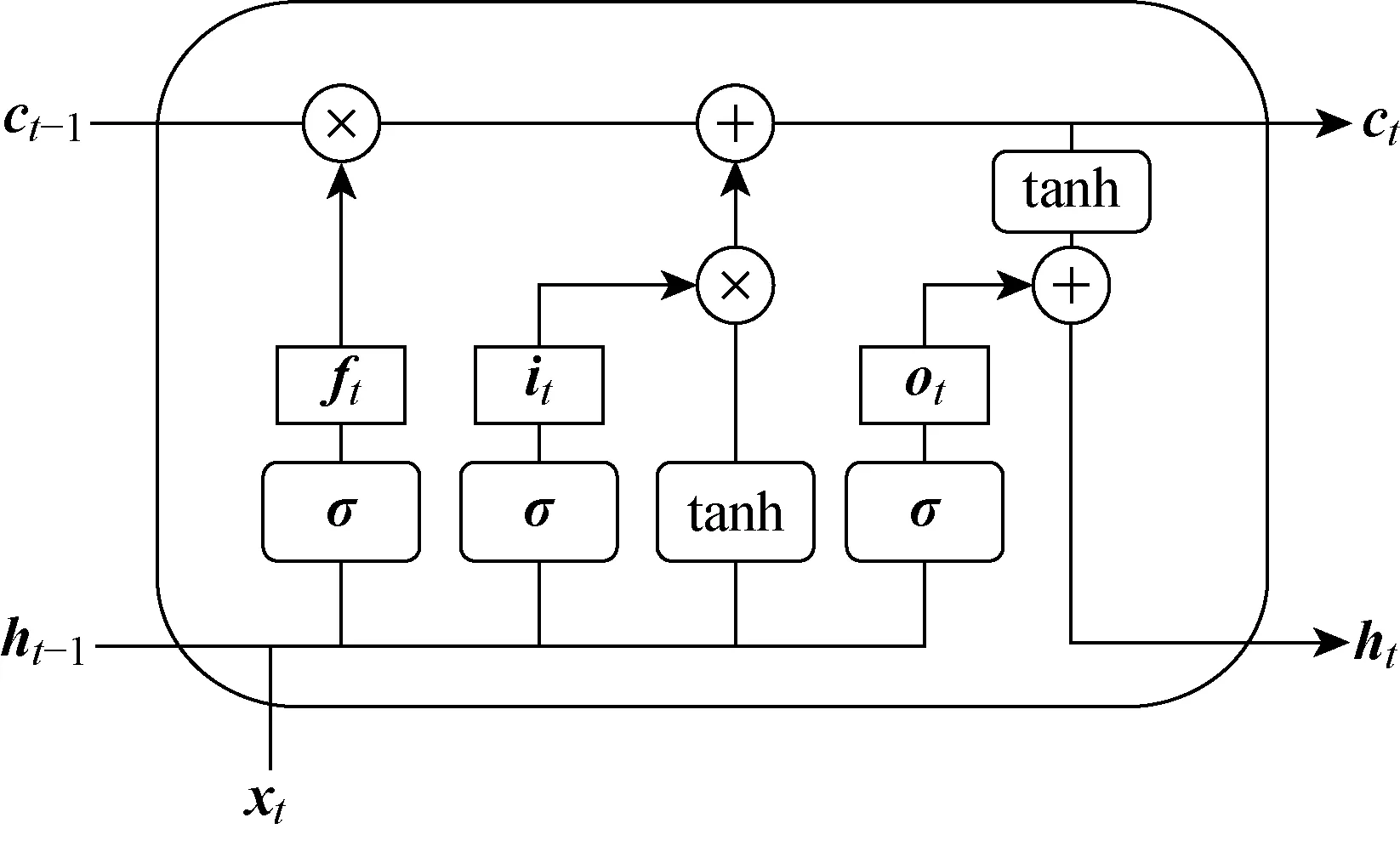
图3 LSTM单元结构Fig.3 LSTM neural network

LSTM网络根据如下规则[6]更新时刻状态:

gi=σ(Wi[ht-1xt]+bi)

(8)

gf=σ(Wf[ht-1xt]+bf)

(9)

go=σ(Wo[ht-1xt]+bo)

(10)

(11)

(12)

ht=go*tanhct

(13)

式中:xt为t时刻的输入向量;ht为t时刻的隐藏状态向量;ct为t时刻的记忆状态向量;gi、gf、go分别代表输入门、遗忘门和输出门;Wi、Wf、Wo、Wc分别代表各连接层的权重矩阵;bi、bf、bo、bc分别代表各连接层的偏置项;σ为sigmoid函数.当前时刻的输入xt,上一时刻的隐藏状态ht-1以及上一时刻的记忆状态ct-1依次通过上述3个门控单元gi、gf和go进行计算,得到当前时刻的隐藏状态ht和记忆状态ct,并作为下一时间步的输入继续推进,门控单元内的权重矩阵、隐藏状态和记忆状态也随之不断更新,从而实现对序列信息的训练学习.

1.4 CNN-LSTM船舶运动极值预报模型

为充分发掘船舶运动的各个模态间可能存在潜在的映射关系,本文构造了基于多维数据输入的CNN-LSTM预报模型,如图4所示.图中:ReLU为激活函数,表达式f(x)=max{0,x};Dropout层为随机失活层,通过随机使一定比例神经元失活的方式防止出现参数过拟合.在对一系列超参数组进行初步测试后,选取其中表现最优的一组作为模型参数,如表1所示.

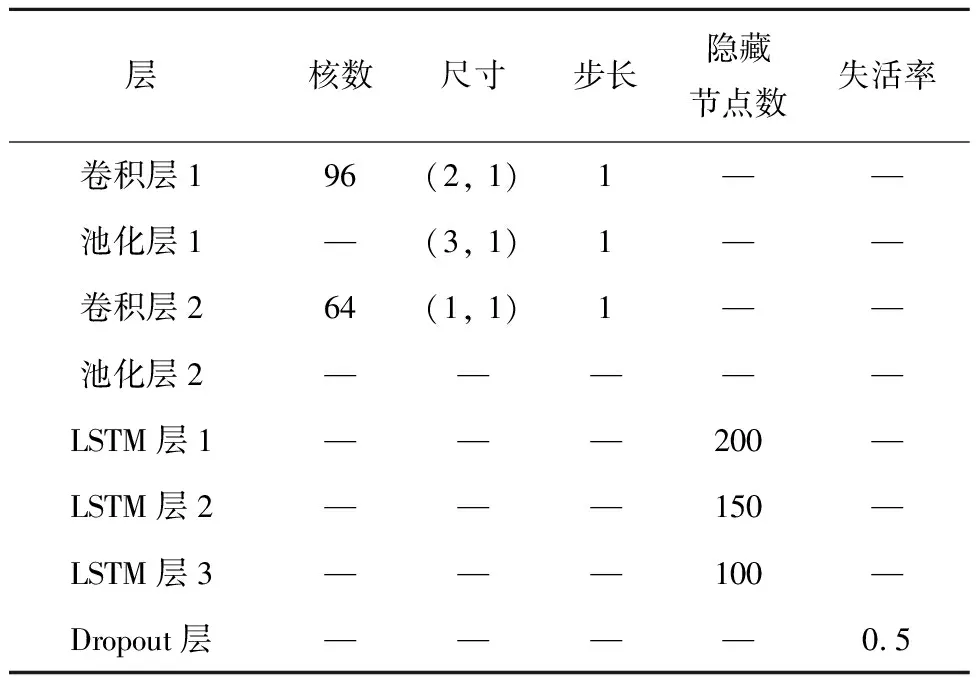
表1 CNN-LSTM模型具体参数Tab.1 Parameters of CNN-LSTM model

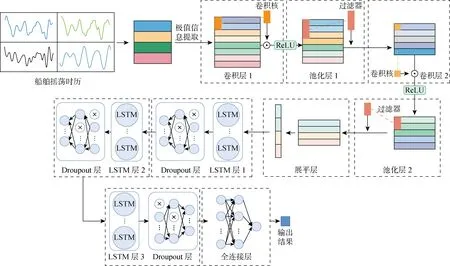
图4 CNN-LSTM预报模型结构Fig.4 Structure of CNN-LSTM model

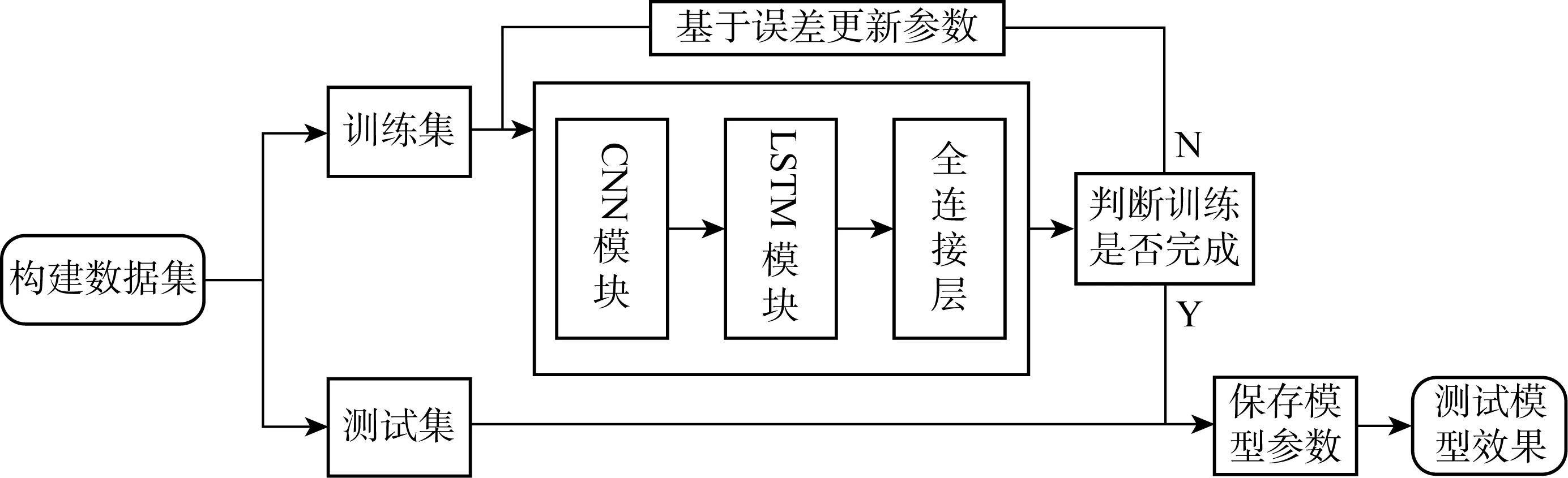
图5 CNN-LSTM预报模型计算流程Fig.5 Calculation process of CNN-LSTM model

本文采用误差反传算法训练模型参数,损失函数取均方误差(Mean Squared Error, MSE),优化器为Adam,初始学习率为0.001,迭代总数为1 200次,训练批量大小为10.选取数据集的前95%为训练集,后5%为测试集.依赖步数l=30,向后预报步数k分别取1, 2.

2 S175船运动预报结果与分析

2.1 数据集生成

本文以S175集装箱船为对象,其主尺度参数为:船长175 m,船宽25.4 m,吃水9.5 m,排水体积 23 680 m3,方形系数0.572.通过海洋系统模拟器 (Marine Systems Simulator,MSS)软件[15]计算生成其迎浪0航速下垂荡、横摇、纵摇、首摇4个自由度的摇荡时间序列,分别记为X3、X4、X5、X6,以船舶及海上平台作业时最为关注的X3、X4、X5为3个目标维度.波浪基于Jonswap谱生成,其表达式[16]如下:

(14)

式中:h1/3为有义波高;T1为特征周期;ωp为谱峰频率;θ为成分波与平均浪向之间的夹角.波浪相关参数为:有义波高5 m,特征周期9.7 m,谱峰频率 0.6 rad/s,平均浪向180°,频率区间数50,浪向区间数20.为保证预报结果的一般性,该参数为随机选取,后续使用的船舶运动数据均基于该组参数生成.

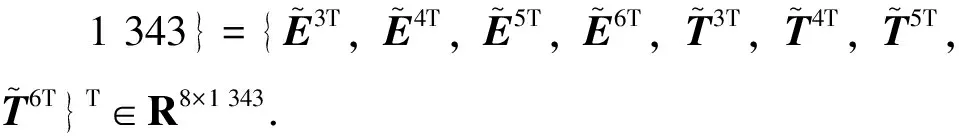
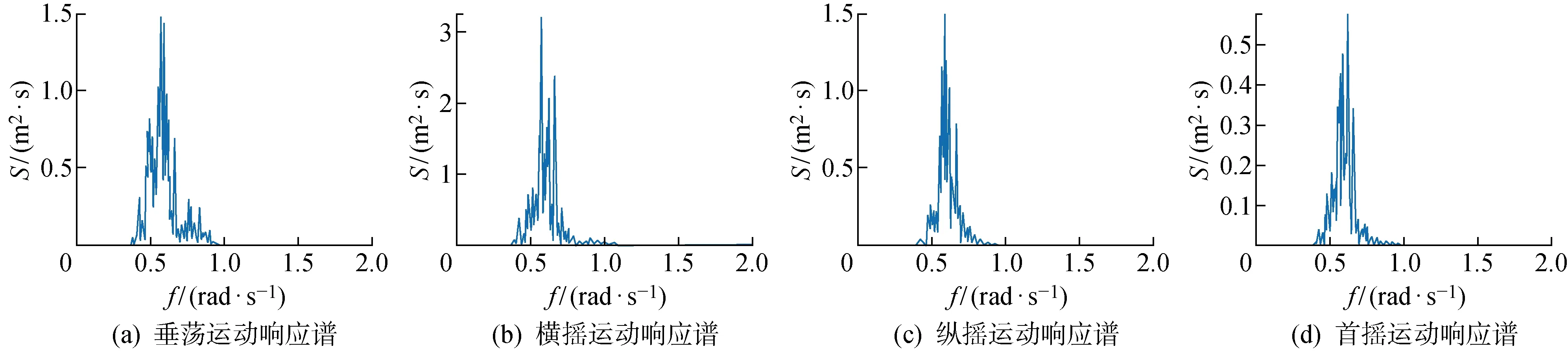
图6 四自由度运动响应谱Fig.6 Motion response spectrum of four degrees of freedom

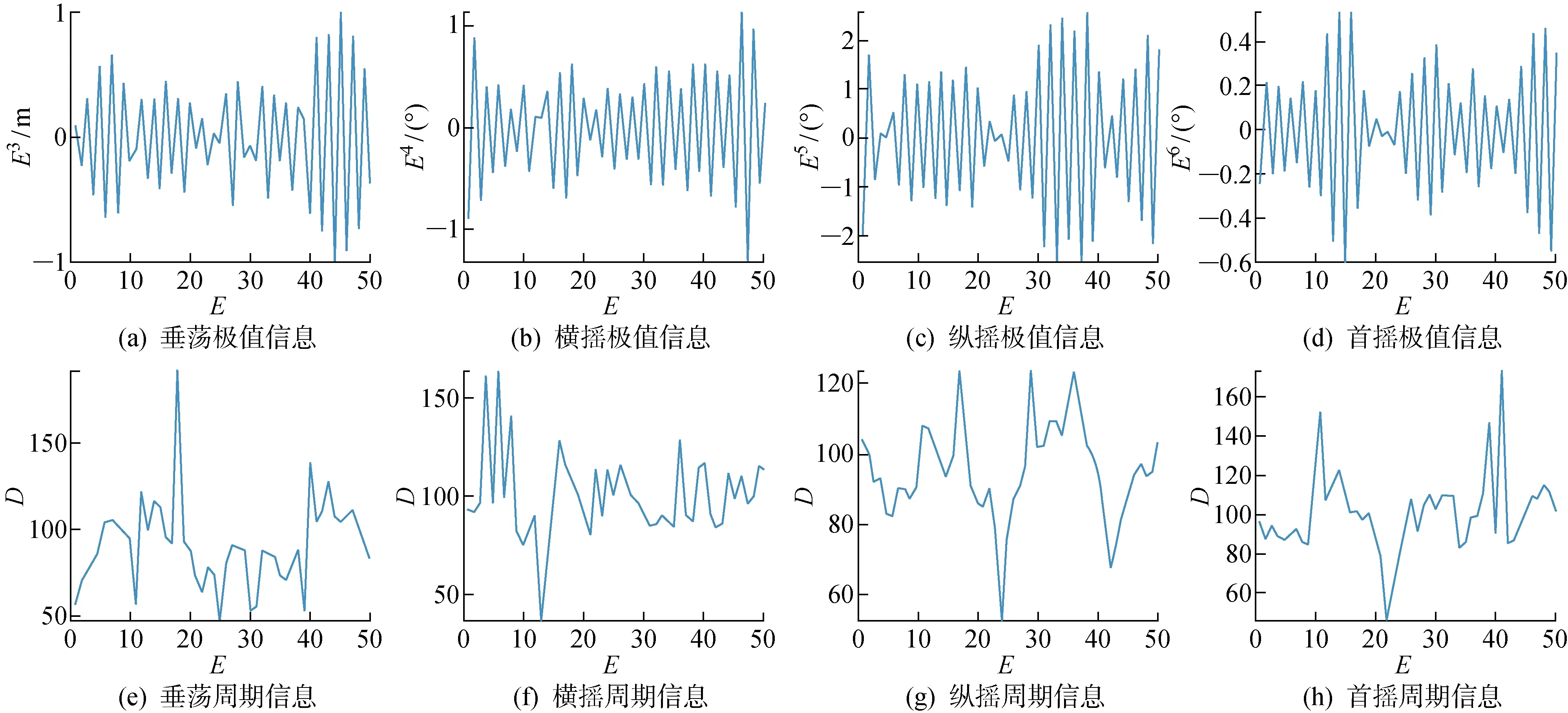
图7 数据集局部图像(前50个点)Fig.7 Image of Local dataset (top 50 points)

2.2 模型评价

2.2.1模型评价指标 为分析模型的预报效果,本文选取平均绝对误差(Mean Absolute Error,eMAE)、均方误差(Mean Squared Error,eMSE)、均方根误差(Root Mean Squared Error,eRMSE)和相关系数(Correlation Coefficient,r)4个指标进行评估.以上均为时间序列预测领域的通用评价指标,具有一定的普适性.各指标由下式计算:

(15)

(16)

(17)

(18)

2.2.2对照模型 为进一步验证预报性能,本文设置了两种对照模型.模型1的基础框架为前述CNN-LSTM模型的LSTM部分,模型2在模型1的基础上将LSTM单元替换为GRU[17].GRU将LSTM的输入门和遗忘门合并更新门,其待训练参数少于LSTM.

2.3 仿真结果与分析

分别使用上述CNN-LSTM、LSTM、GRU模型对S175船在波浪中3个自由度的摇荡运动进行极值信息预报.各模型向后预报一个极值时的结果如图8所示.采用2.2.1中的评价指标评估各模型在测试集上的预报误差,结果如表2所示.

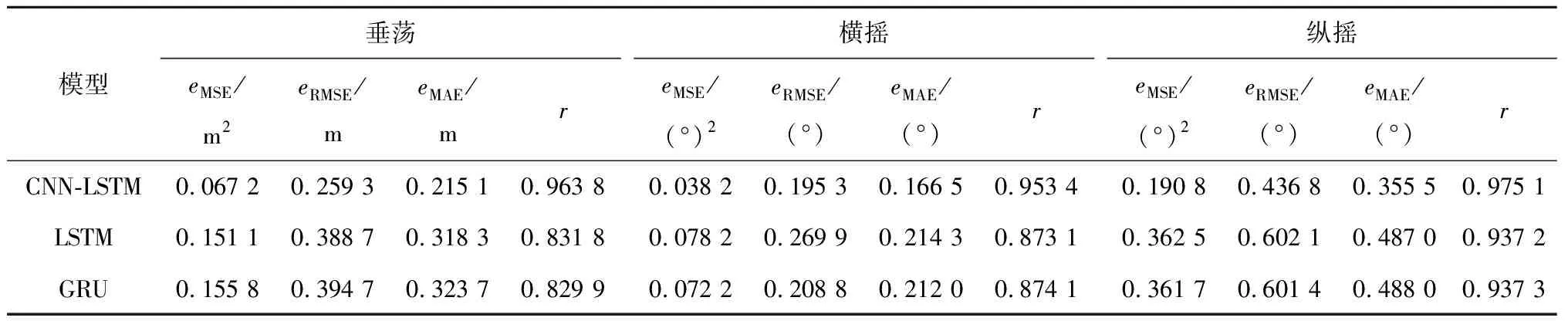
表2 各模型单步预报误差Tab.2 Single step prediction error

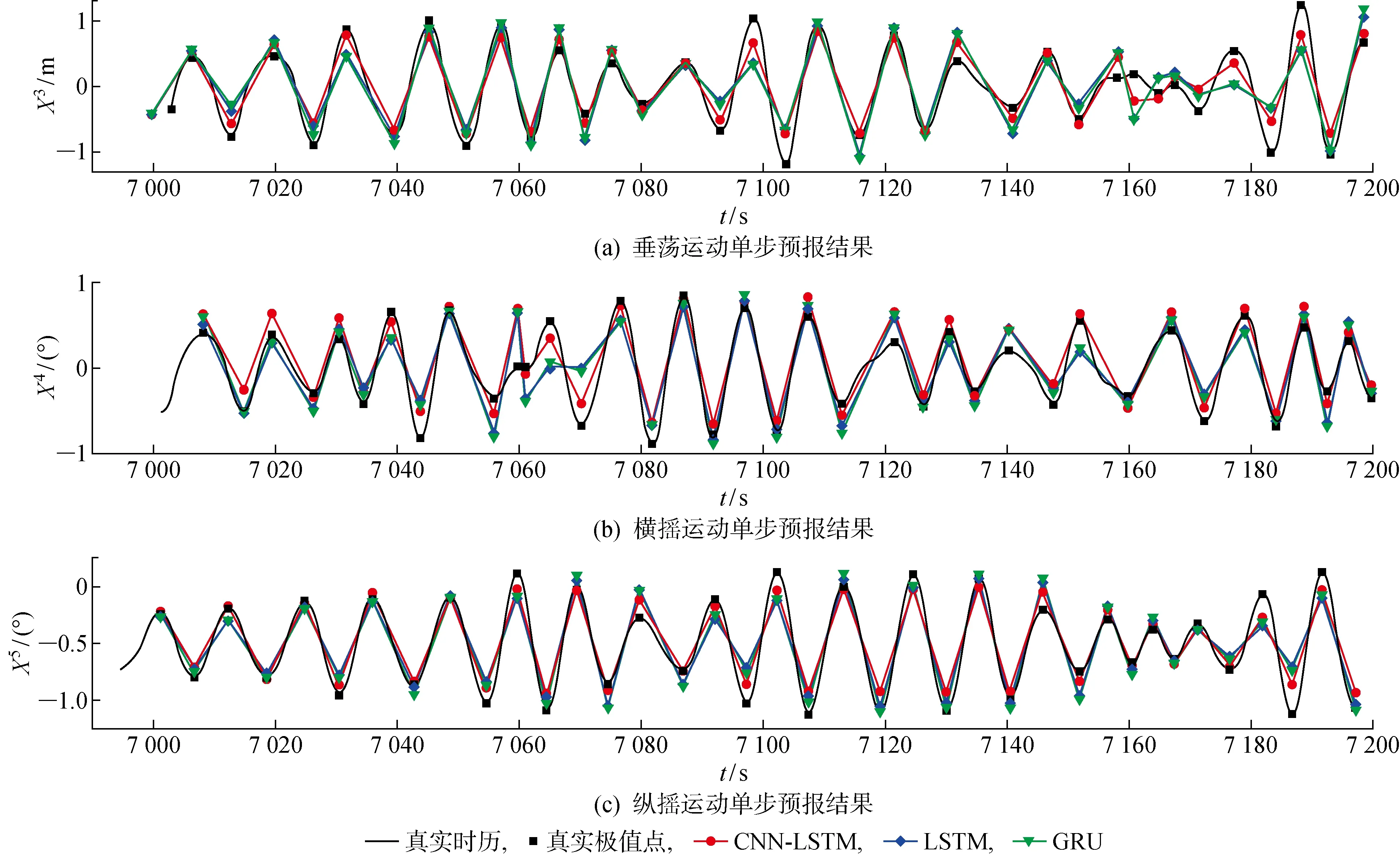
图8 各模型单步预报结果Fig.8 Results of single step prediction

本文提出的CNN-LSTM模型在各项误差指标上都优于LSTM和GRU模型,以MSE为标准,3个自由度下的预报效果比LSTM模型分别提升了55.5%、51.1%和47.4%,比GRU模型分别提升了56.9%、47.1%和47.2%.以MAE为标准,3个自由度下的预报效果比LSTM模型分别提升了32.4%、22.3%和27.1%,比GRU模型分别提升了33.5%、21.5%和27.1%.从图像上看,CNN-LSTM模型的预报幅值普遍比其余两种模型更接近真实值;而在序列出现非平稳波动处,LSTM和GRU模型的预报结果偏差较大,而CNN-LSTM模型仍能较好地给出预报结果.可见,CNN-LSTM 模型中卷积层和池化层对数据特征信息的提取显著提升了预报性能,该模型能够基于历史数据较为精确地预报下一极值点的信息.

CNN-LSTM模型提前2步的极值预报结果如图9所示.提前2步预报的误差情况如表3所示.

表3 CNN-LSTM模型多步预报误差Tab.3 Multi-step prediction error

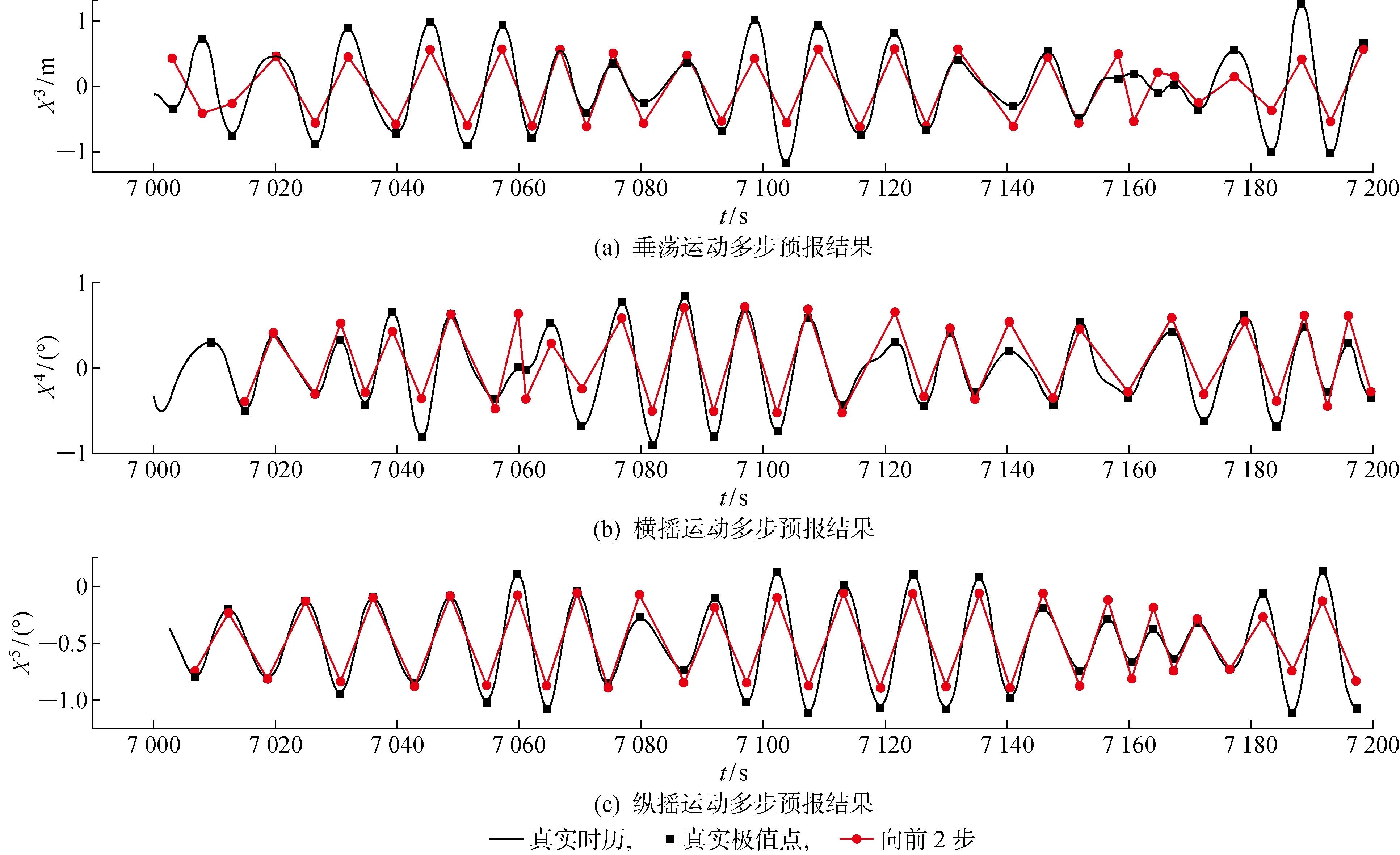
图9 CNN-LSTM模型多步预报结果Fig.9 Results of multi-step prediction

可见,CNN-LSTM模型的多步预报精度有所下降,同时预报结果出现了一定的滞后性.这是由于序列本身具有非平稳非线性的特点,随着预报步数的增加,输入值与预报值间的潜在规律更加复杂,训练难度也因此上升.图10所示为各自由度预报结果与实际观测值间的相关性分析.其中,Xp表示预测值,Xr表示真实值.可见,预报结果的变化趋势仍与实际情况吻合较好,提前2步的3自由度预报值与实际值的平均相关系数分别为81.8%、90.7%和94.6%,能够满足实际需求.

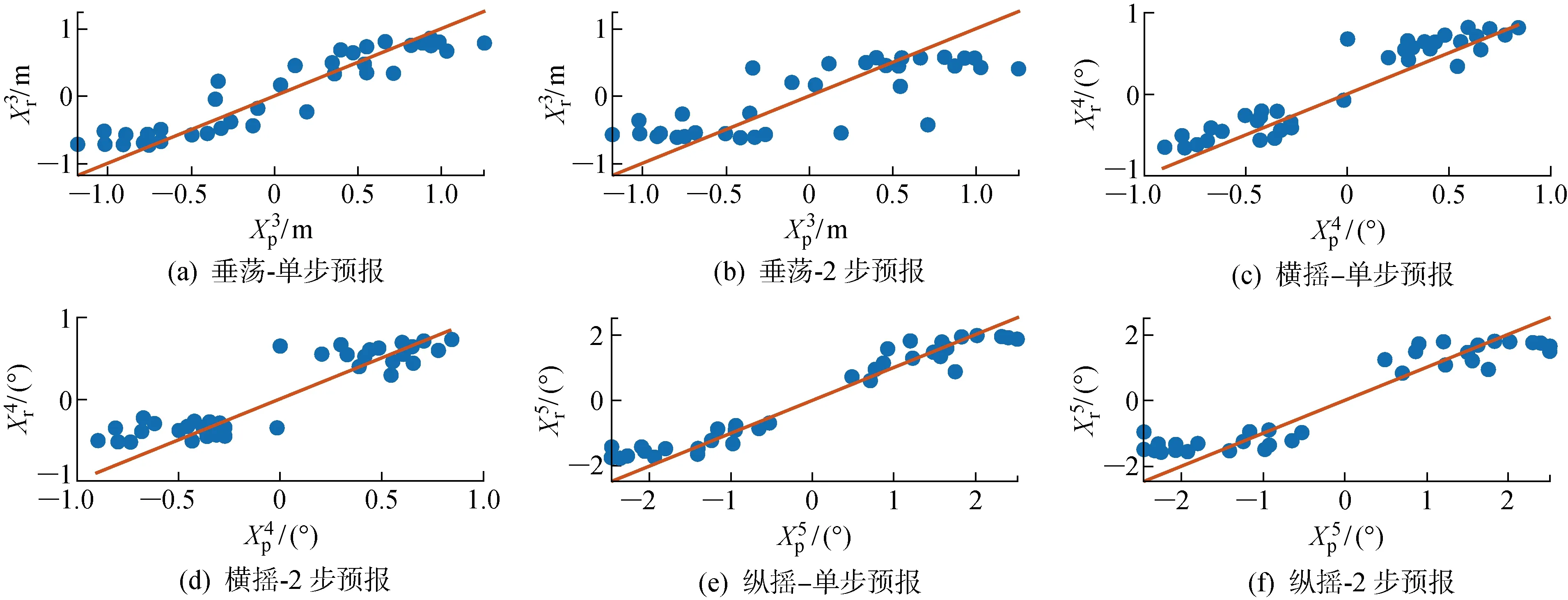
图10 预报结果与实际值的相关性分析Fig.10 Correlation analysis of prediction results and actual values

3 结论

以船舶摇荡运动的极值信息为预报目标,以船舶4个自由度的运动时间序列为原始数据,构造了一种CNN-LSTM组合预报模型.针对S175船的验证结果表明,该模型在单步预报时精度良好,各项误差指标相较LSTM和GRU模型均有明显提升,垂荡、横摇、纵摇3个自由度下的MSE较LSTM模型分别提升了55.5%、51.1%和47.4%,较GRU模型分别提升了56.9%、47.1%和47.2%;MAE较LSTM模型分别提升了32.4%、22.3%和27.1%,较GRU模型分别提升了33.5%、21.5%和27.1%.在多步预报时误差指标略有下降,但预报趋势仍能与实际值保持吻合,提前2步的3自由度预报值与实际值的平均相关系数分别为81.8%、90.7%和94.6%.

本文提出的预报模型具有以下优点:① 结合船舶运动响应谱进行数据前处理,有效提取了船舶运动极值信息,同时抑制了高频噪声的影响;② 通过CNN模块发掘学习各维度数据间的潜在联系,充分利用了已知信息,并提高了预报精度;③ 模型预报效果良好,仿真实验表明该模型能够准确预报未来1～2个周期内船舶运动的极值信息,且预测指标明显优于对照模型.在此基础上,未来可进一步探究该模型针对实测复杂海况下的预报效果,并实现完整的在线预报流程.该工作对于诸如舰载机起降、海上平台安装等场景具有重要应用价值,同时也可为波浪信息预报等时间序列预测问题提供参考.