基于浸入边界法的高解析度CFD-DEM流固耦合方法

毛 佳, 肖景文, 赵兰浩, 底瑛棠

(河海大学 水利水电学院,南京 210098)

流固耦合问题常见于不同工程领域,根据固体的物理性质,可划分为流体与连续介质、流体与非连续介质间的流固耦合问题.目前,处理流体与连续介质间的流固耦合问题的数值模拟技术已较为成熟,广泛应用于水利工程[1]、船舶工程[2]等领域;而流体与非连续介质间的流固耦合,例如滑坡涌浪[3]、冰区航行[4]等问题的数值模拟仍具有较大的挑战性,主要难点在于固体运动过程中流固耦合界面的准确描述.

有研究者采用特殊的网格处理技术模拟流固耦合运动界面,如动网格[5-6]、嵌套网格[7]等.但由于固体运动的无规律性以及运动过程中相互间的碰撞,采用动网格方法时将会产生网格扭曲,甚至网格拓扑结构发生变化的问题.嵌套网格方法虽然适应性较好,但是此方法在运动固体周围设置的部件网格限制了其应用范围,当计算大量块体碰撞的问题时,各个部件网格将发生重叠,导致计算难以顺利进行.因此,这些网格处理技术只适用于模拟少量块体的非碰撞流固耦合问题,而对于涉及大量离散块体的流固耦合问题则存在明显的局限性.

考虑到流固耦合运动界面的模拟难度较高,有研究者提出简化的欧拉-欧拉多相流模型[8],采用流体本构模型模拟离散块体,使得固体和流体间的界面成为内部界面,避免了采用特殊的措施处理流体域的移动且未知的边界.然而,此类方法不能体现固体的非连续性,较适用于解决固体呈现出显著流体化特征的问题.实际上,流体与固体具有截然不同的物理力学性质,需要采用不同的方程进行描述[9],因此,有研究者提出了属于欧拉-拉格朗日方法的离散相模型(DPM)[10].此方法能够考虑固体的非连续性,但由于无法模拟固体间的相互碰撞,只能用于模拟稀疏两相流问题.

近年来,国内外研究者普遍采用耦合数值方法模拟流固耦合问题,即将基于欧拉框架的计算流体力学(CFD)方法与基于拉格朗日框架的离散元法(DEM)耦合,建立CFDEM流固耦合数值模拟方法.目前的耦合方法大多基于经验公式计算流固耦合作用力,实际上可以将这些耦合数值模拟方法看作DPM的一种改进,通常将此类方法称为非解析的(Unresolved)CFDEM耦合方法[11-12].非解析的CFDEM耦合方法是将计算流体力学方法与非连续介质方法相结合进行流固耦合问题研究的一次有益尝试,以简化的方式处理固体与流体的相互作用力,回避了两种介质之间边界移动且未知的问题,能够有效描述非连续介质在流场中的宏观运动规律,具有计算量小的优点.但与实际物理过程相比,该方法仍存在一些明显的不足:① 目前的经验公式仅限于圆形颗粒;② 流固耦合边界条件无法准确满足;③ 多颗粒流固耦合问题中,尾流对颗粒运动的影响难以充分反映.

为了解决非解析流固耦合方法的上述缺点,本文提出高解析度(Resolved)CFD-DEM流固耦合方法.采用Navier-Stokes方程组作为控制方程模拟流体的运动,并在固定网格上采用投影法求解流场运动变量;采用离散单元法模拟非连续固体的任意运动;引入浸入边界法(IBM)表示固体和流体间的移动边界,并计算两者间的相互作用力.通过强耦合迭代求解算法,提高计算的收敛性和稳定性,获得高精度的流场特性,准确反映固体运动过程中的流固耦合界面.

1 CFD-DEM流固耦合方法

相比于基于经验公式的非解析流固耦合方法,本文提出的高解析度方法能够准确反映流固耦合作用力,同时,在流固耦合界面上严格满足速度边界条件,能够在块体周围获得高解析度的流场.本文提出的基于浸入边界法的CFD-DEM流固耦合方法示意图如图1所示.

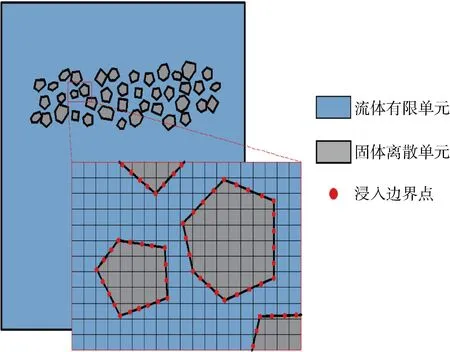
图1 基于浸入边界法的CFD-DEM流固耦合方法示意图Fig.1 Sketch of resolved CFD-DEM algorithm based on immersed boundary method

采用基于欧拉框架的CFD描述流体的运动,采用基于拉格朗日框架的DEM描述固体的运动及碰撞,在离散单元的表面布置浸入边界点,解决固体运动过程中与流体间的移动且未知的边界问题.为了实现流体域与固体域间的强耦合,提出流固耦合系统迭代求解方案.

1.1 流体域数值模拟

在黏性不可压缩Navier-Stokes方程组右端项中引入附加体力项,得到如下控制方程组:

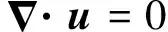
(1)

(2)

式中:u为流场速度;t为时间;p为压力;ρ为密度;fb为体力项;τ为黏性应力张量;f为附加体力项.

在直接力法中,附加体力项由动量方程结合浸入边界点上的速度相容条件推导而来.速度相容条件是指在流体固体交界面上需要满足速度相同条件,即

Un+1=Vn+1

(3)

式中:Un+1表示将笛卡尔网格点上的流体速度插值到浸入边界点上得到的速度;Vn+1表示同一浸入边界点上的固体速度;n表示计算步.

引入插值函数I(φ,Xi),将定义在笛卡尔网格上的物理量插值到浸入边界点上,同时,引入分配函数D(Φ,x),将定义在浸入边界点上的物理量分配到笛卡尔网格上,插值函数与分配函数分别满足如下条件:

(4)

(5)

式中:φ(x)表示定义在笛卡尔网格节点x上的物理量,包括u,p,f等;Φ(Xi)表示定义在浸入边界点Xi上的物理量;gb表示笛卡尔网格点的集合;NIBP为插值计算某笛卡尔网格节点上物理量时所涉及到的浸入边界点数目;ΔSi表示浸入边界点的控制域;δ表示狄拉克函数,在二维情况下满足δ(x)=d(x)d(y),

(6)

h取为网格尺寸的倍数;r表示有限元网格节点与浸入边界点的距离.结合式(4)～(6),可实现物理量的插值与分配.

基于特征线法,式(2)的时间离散格式如下:

Δu=Kn+Rn+1+fn+1Δt

(7)

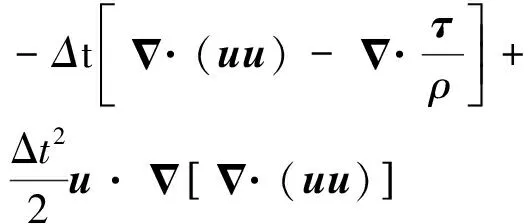
(8)

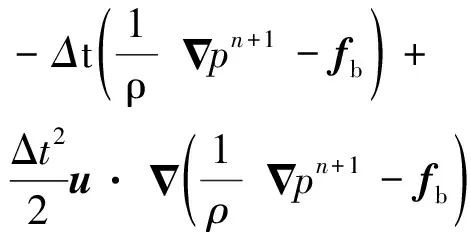
(9)

在此基础上,将第n个时间步的速度增量分为两个部分:

Δu*=Kn+fn+1Δt

(10)

Δu**=Rn+1

(11)

将中间速度场增量式(10)与速度场增量的修正量式(11)代入速度边界条件Vn+1=Un+1中,整理可得:

fn+1Δt=D[I(fn+1Δt)]=

D[Vn+1-I(un+Kn+Rn+1)]

(12)

由式(12)可见,附加体力项与速度场、压力场耦合,因此需要通过迭代计算求解上述三类未知量,具体步骤如下.

步骤1忽略压力及附加体力项,计算中间速度场u*,K,u*,K=un+Kn.

步骤2计算压力场增量Δpn,k及附加体力项fn+1,k.令pn+1,0=pn,fn+1, 0=0,k=1.

步骤2.1根据附加体力项的计算公式计算fn+1,k.

值得注意的是,当浸入边界点与网格点重合,式(12)中的fn+1Δt=D[I(fn+1Δt)]成立,附加体力项的计算无需迭代.然而,通常情况下,浸入边界点与网格点不重合,通过单次计算附加体力项并不能满足速度边界条件,因此需要迭代求解体力项.令fn+1,k,0=fn+1, k-1,i=1,根据fn+1,k,iΔt=fn+1,k,i-1×Δt+D[Vn+1-I(un+Kn+Rn+1+fn+1,k,i-1Δt)]计算fn+1, k, i.在此基础上,计算‖Vn+1-I(un+Kn+Rn+1+fn+1, k, i-1Δt)‖,进行收敛性判断,其中‖·‖表示任一范数,如果范数小于容差ε,则结束步骤2.1,否则令i=i+1,迭代计算直到满足收敛条件.最终,fn+1, k=fn+1, k, i.

步骤2.2更新中间速度场u*,计算式为u*=u*, K+fn+1,kΔt.

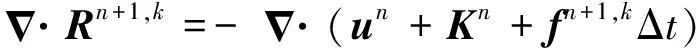
步骤2.4收敛性检查.计算‖I(un+Kn+Rn+1,k)-I(un+Kn+Rn+1,k-1)‖,如果小于容差ε,则满足收敛性检查,结束步骤2的迭代计算,否则,令k=k+1,重复步骤2.1～2.4,直到满足收敛条件.

步骤3更新压力场pn+1=pn+Δpn, k,校正速度场un+1=u*+Rn+1,k.

1.2 固体域的数值模拟

根据牛顿第二定律,固体运动的控制方程如下:

(13)

(14)

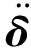
Fc可分为法向接触力Fcn和切向接触力Fct,Fcn的计算式如下:

Fcn=pf∮Sβc∩βtnSβc∩βt(φc-φt)dS

(15)

式中:pf为罚函数;βc为接触单元;βt为目标单元;n为重叠域边界的单位外法向向量;φc、φt分别为定义在接触单元、目标单元上任一点的势函数[13];S为重叠区域.

根据力-位移法则计算切向接触力,具体地,通过计算单元所受法向接触力合力及其作用点,并依据法向接触力合力的方向确定当前时间步切向力方向,以位移增量法计算切向接触力大小[14],详细步骤如下:

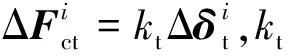
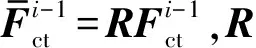
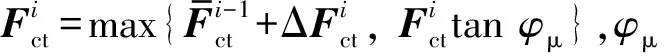
1.3 流固耦合系统迭代求解方案

为了实现流体域与固体域间的强耦合,提高计算的收敛性和稳定性,获得高精度的流场特性,准确反映固体运动过程中的流固耦合界面,提出了流固耦合系统迭代求解方案.为简化起见,流体和固体控制方程迭代格式记为

(Δun, k, Δpn, k)=Rf

(16)

Δδn,k=Rs

(17)

式中:Rf表示流体方程右端项,与un、pn、δn+1, k-1相关;Rs表示固体方程右端项,与δn、un+1, k、pn+1, k相关.

假设第n步计算已经完成,现在进入第n+1步的第k次迭代,执行过程如下:

步骤1求解流体方程,更新速度场un+1, k与压力场pn+1, k.

步骤2求解固体方程,更新固体的位置δn+1, k.

步骤3收敛性检查.计算‖Δζn, k-Δζn, k-1‖,如果小于容差εζ,则满足收敛性检查,结束当前时间步的流固耦合系统迭代计算,否则,令k=k+1,重复步骤1～3,直到满足收敛条件.其中,ζ可取为变量Δu、Δp以及Δδ,εζ为对应于各变量ζ的给定的小值.

2 数值算例分析

2.1 圆柱绕流涡激振动

圆柱绕流涡激振动[15-16]被广泛用于验证流固耦合算法解决固体平动耦合问题的准确性.圆柱具有水平向x及竖直向y两个方向的自由度,运动方程如下:

(18)

(19)

式中:ξ为阻尼比;U*为折合流速;D为圆柱直径;m*=ms/mf为质量比,ms、mf分别为圆柱质量与同等体积下的流体质量;CL、CD分别为升力系数、阻力系数;X、Y为圆柱无量纲位移,分别满足X=x/D、Y=y/D.

计算域大小为[-15D, 45D]×[-20D, 20D],初始时刻圆柱圆心坐标为(0, 0).雷诺数Re=200,ξ=0.01,U*=5.0,m*=4/π.计算域左侧边界为均匀入流边界,右侧边界为自由出流边界,上、下边界为滑移固壁.为分析网格敏感性,采用了3种网格尺寸,分别记为L1、L2及L3,对应地,计算域离散为204×112、408×224及816×448个非结构化四边形单元,圆柱周围的网格尺寸分别为D/20、D/40及D/80,在圆柱表面布置753个浸入边界点.

固定圆柱直至下游产生稳定的卡门涡街,此后释放圆柱,可在圆柱下游观察到如图2所示的涡(图中Ω为涡量).圆柱振动频率为0.187,与漩涡脱落频率接近.

图2 圆柱下游涡量场(L3)Fig.2 Vortexes field downstream of cylinder (L3)

由于流场拖曳力的作用,圆柱的振动中心偏离(0, 0),本文方法计算得到的圆柱振动中心为(0.632D, 0),与参考文献[15]中的(0.62D, 0)接近.为方便对比,将圆柱振动中心平移至(0, 0),在此基础上绘制了圆柱“8字形”振动轨迹对比图,如图3所示.由于L1网格较粗,无法精确捕捉下游脱落的漩涡,所以使得x方向与y方向的位移较小,当采用较密网格L2、L3时,本文计算结果与前人的贴体网格计算结果[15]、基于浸入边界法的强耦合数值模拟结果[16]极为接近,一方面说明了加密网格可显著提高数值计算的精度,另一方面说明了本文方法模拟固体平动耦合问题的准确性.

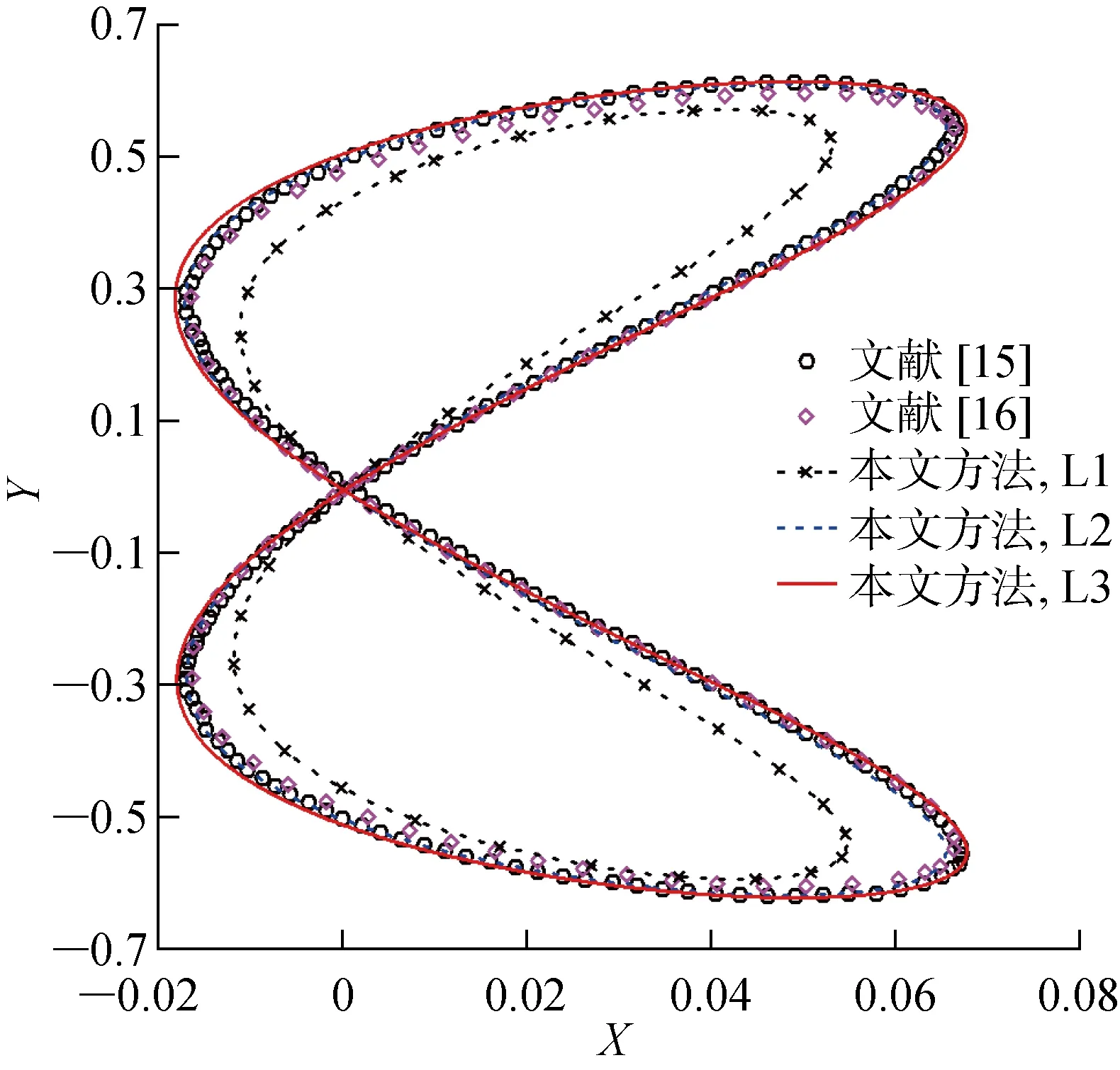
图3 圆柱中心振动轨迹Fig.3 Centerline displacement phase plot

为说明流固耦合迭代对计算效率的影响,比较了计算时间t=3 s时,迭代次数取1和3的耗时.迭代1次的工况耗时为 7 899.38 s,迭代3次的工况耗时为 23 150.77 s,约为迭代1次工况耗时的2.9倍.可见,增加流固耦合迭代次数对计算效率有显著影响.然而,对于流场的变化或流固耦合作用剧烈的强耦合问题,若采用弱耦合求解格式,即用上一个时间步的力来求解当前步的运动,即使流体、固体的计算收敛,仍不能代表流固耦合系统一定收敛.因此,对于此类问题,即使会损失计算效率,也必须采用强耦合求解格式来保证计算精度.

2.2 方块驰振

为说明本文方法计算固体转动耦合问题的准确性,计算了经典的方块驰振问题[16-18],参考文献[17]中采用贴体网格计算,参考文献[16,18]中采用基于浸入边界法的流固耦合数值模拟方法计算,提供了强耦合模拟结果.方块宽度为L,厚度为Ds,运动方程如下:

(20)

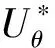
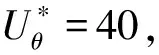
固定方块直至下游产生稳定脱落的涡,此后释放方块.方块转动过程中的流场涡量示意图如图4所示.当方块转动角度为正最大值及负最大值时,涡量场呈反对称状态,如图4(a)、图4(c)所示.

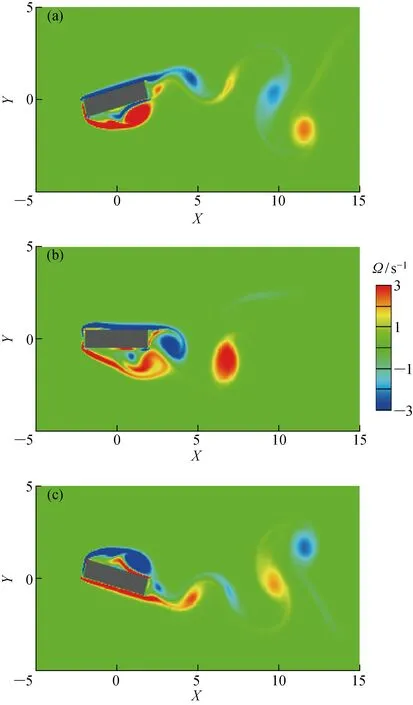
图4 方块转动过程中的瞬时涡量场Fig.4 Instantaneous vorticity surrounding rectangular rigid body

表1给出了本文计算得到的方块最大转角θmax及转动频率frot,当前方法得出的最大转角为15.4°,与文献[16]中的结果误差不超过4.4%;当前方法得出的转动频率为0.019 2,与文献[18]中的结果误差不超过3.1%.

表1 方块最大转角θmax及转动频率frot

图5中绘制了方块转角变化过程对比图.图中:U为流体自由流速.由于已有参考文献中方块释放时间不一致,初始阶段的方块运动有一定的差异,但 是当转动逐渐发展稳定之后,各结果间的吻合度较高,说明了本文方法模拟转动耦合问题的准确性.

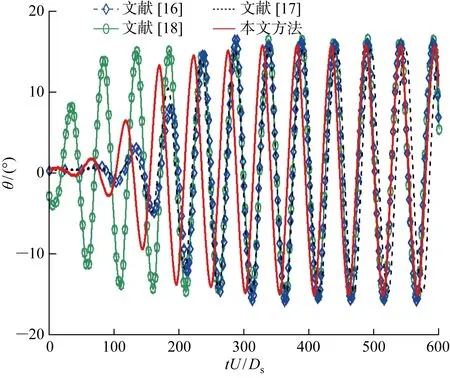
图5 方块转角变化过程Fig.5 Evolution of rotational angle

2.3 多块体沉降

为说明本文方法模拟流体与多固体间的流固耦合作用及固体间碰撞作用的能力,模拟了多块体沉降问题.

计算域尺寸为[0, 10 m]×[0, 10 m],采用两类正方形块体,共计28个,边长分别为0.698 m、0.548 m,在重力作用下自由下落.初始时刻位置如图6所示.A点坐标为(0.802 m, 7.945 m),B点坐标为(1.427 m, 6.750 m),同层块体间的x向距离均为1.100 m,相邻两层块体间y向距离为1.120 m.水体密度为1 000 kg/m3,动力黏性为0.01 kg/(m·s),块体密度为 2 600 kg/m3.计算域离散为480×480个结构化四边形单元,在边长为 0.698 m、0.548 m 的块体表面分别布置404、320个浸入边界点.本算例中所有边界均设为无滑固壁.

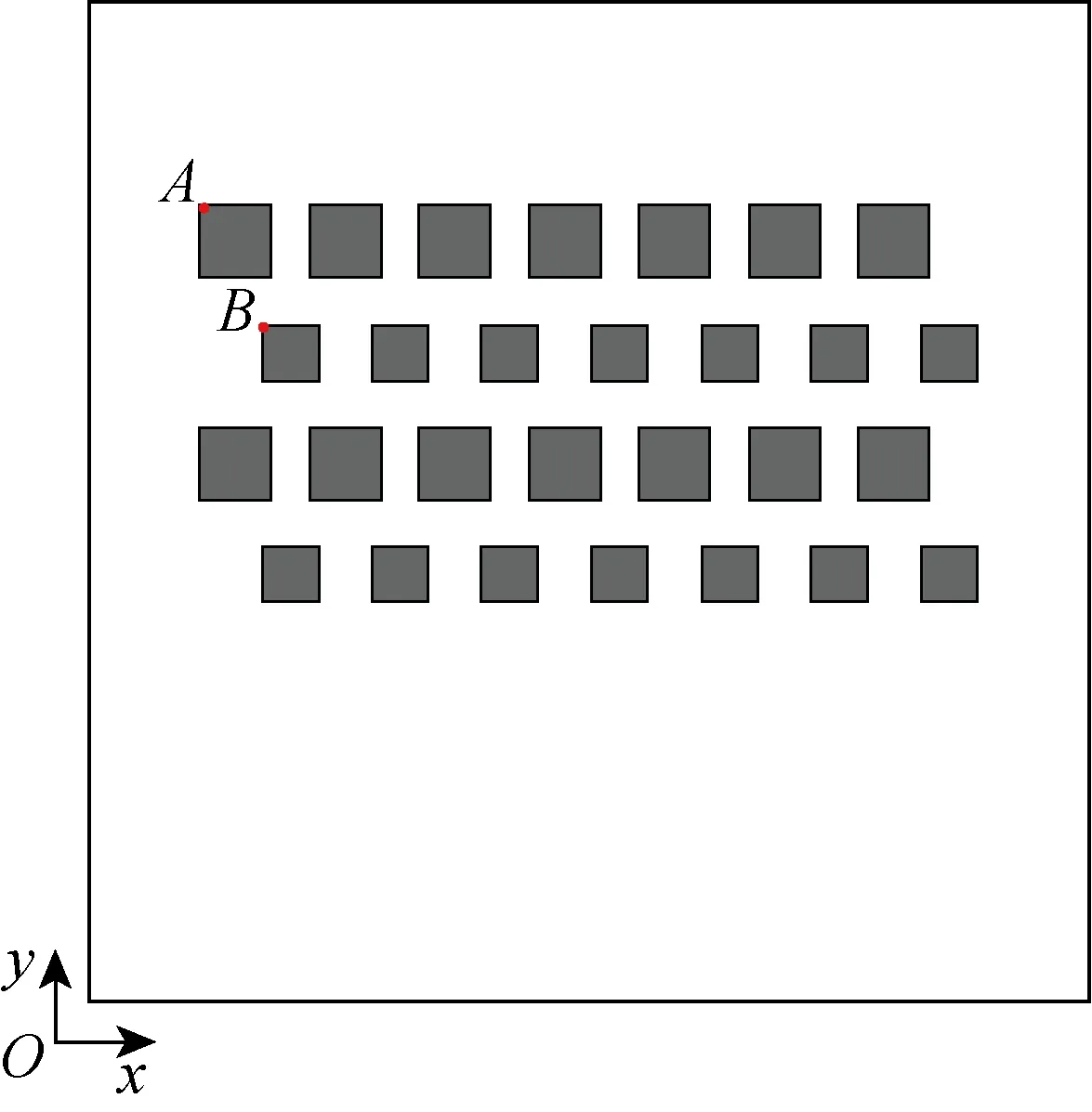
图6 块体初始时刻位置Fig.6 Initial positions of solids

图7中给出了块体运动速度(v)及流体域速度矢量场变化过程.初始阶段(见图7(a)),水体受块体运动扰动的同时,向块体施加了作用力.随着块体的进一步沉降,水体和块体间的相互作用逐渐增强(见图7(b)～图7(d)),此阶段在块体周围可以观察到大量的涡,受涡的影响,块体在沉降过程中伴随着转动.部分块体在2.8 s左右开始接触计算域底部,此后流场的扰动显著降低(见图7(e)～图7(f)).此算例说明了本文方法不限于模拟流体和圆形颗粒的相互作用,能够描述流场的复杂变化及固体间的碰撞,可实现复杂流固耦合问题中固体运动界面的准确描述.

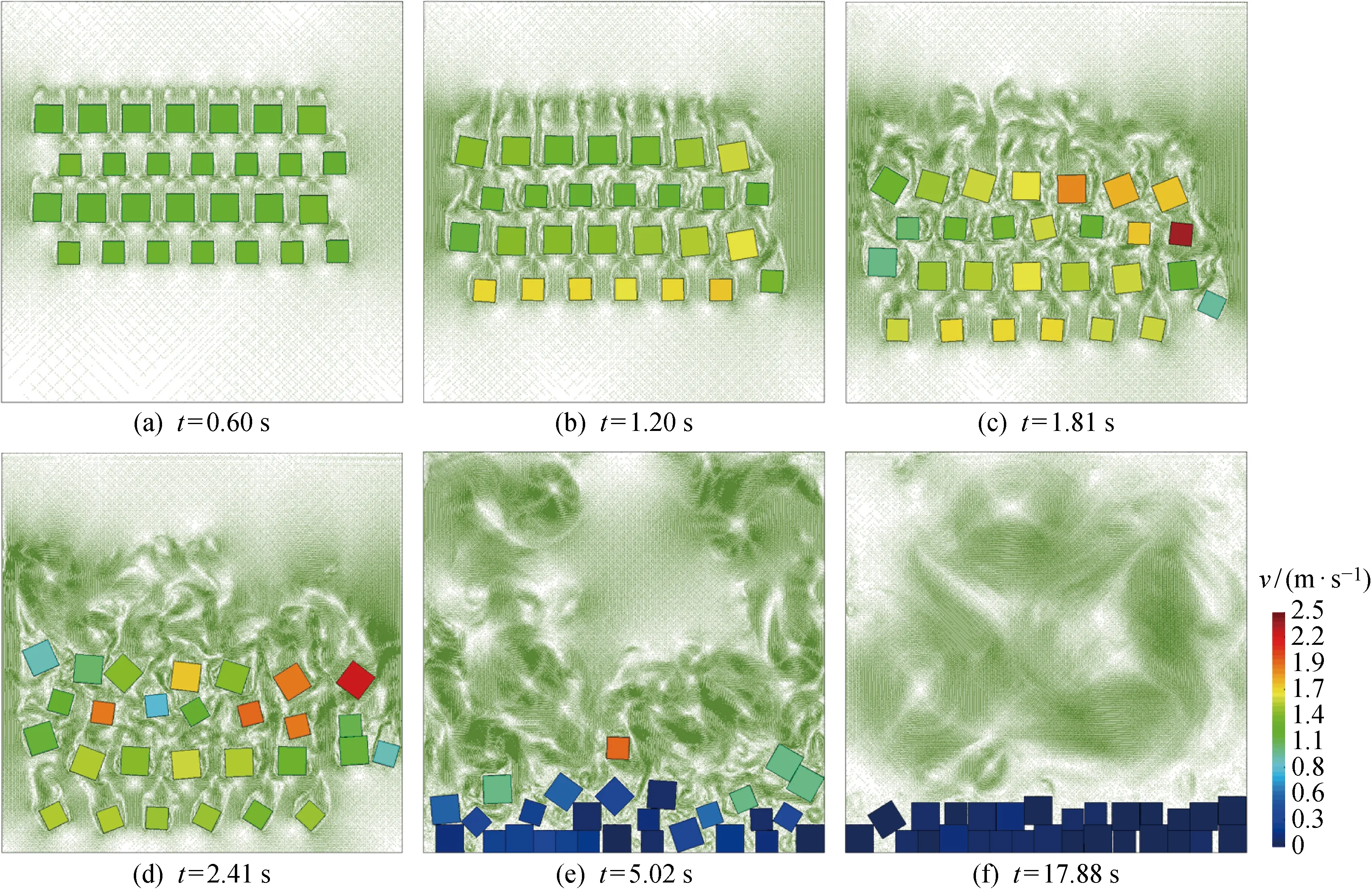
图7 块体运动速度及流体域速度矢量场变化过程Fig.7 Instantaneous velocity vector of fluid field and position of rigid bodies

3 结论

提出了基于浸入边界法的高解析度CFD-DEM流固耦合方法,主要结论如下:

(1) 区别于非解析CFDEM耦合方法依赖于经验公式计算流固耦合作用力,新方法采用浸入边界法表示固体和流体间的移动边界,并计算两者间的相互作用力.

(2) 计算了圆柱绕流涡激振动、方块驰振两个经典算例,并与已有数值计算结果进行比较,验证了新方法计算平动耦合问题、转动耦合问题的准确性.

(3) 模拟了多块体沉降问题,说明了新方法不局限于圆形颗粒,可以有效描述复杂流固耦合问题中的运动界面,获得高解析度的流场.