整体思想在解高考题中绽放
——以2022年浙江高考解答题为例
洪昌强
(台州市第一中学,浙江 台州 318000)
很多学生认为2022年浙江高考试题运算量较大,直接影响了高考得分.试题的运算量大在何处?造成运算困难的原因又在何处?笔者对各个试题的解题思维过程进行分析,不难发现学生在处理问题时,缺乏整体思想.下面对浙江卷的5道解答题进行剖析.
1 善用关系,化繁为简
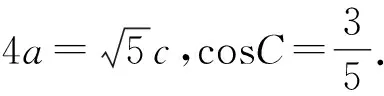
(1)求sinA的值;
(2)若b=11,求△ABC的面积.


图1 2022年浙江数学高考18题图

评注此题多数学生直接利用正弦、余弦定理进行求解,若从几何图形的整体性出发,根据条件所提供的信息,从整体上把握三角形边、角之间的内在关系,就能轻松、简捷地得到结果.
例2 (2022年浙江省数学高考第20题第(2)问)已知等差数列{an}的首项a1=-1,公差d>1.记{an}的前n项和为Sn(n∈N*).若对于每个n∈N*,存在实数cn,使an+cn,an+1+4cn,an+2+15cn成等比数列,求d的取值范围.
分析从条件知{an}是等差数列,且a1=-1,公差d>1,多数人受此影响,将an,an+1,an+2用n,d进行表示,即
an=-1+(n-1)d,
an+1=-1+nd,
an+2=-1+(n+1)d.
代入(an+1+4cn)2=(an+cn)(an+2+15cn),展开后发现等式中项数较多,运算量较大.对于运算能力薄弱的学生,很难完成接下去的推理过程. 若从整体思想考虑,先直接将(an+1+4cn)2=(an+cn)·(an+2+15cn)展开,整理成
根据等差数列的性质,对局部先进行化简,即
8an+1-15an-an+2=6d-8an.


因为a1=-1,公差d>1,
故n≥3时,an≥d都成立.
对于n=1时,△≥0显然成立.
当n=2时,由△≥0,解得1 所以d的取值范围为(1,2]. 评注本题充分利用an,an+1,an+2三者之间的特殊关系,对“an,an+1,an+2”先采用按兵不动的方法,保持“原貌”的整体性,这样在等式变形时,摆脱局部细节中一时难以弄清的数量关系的纠缠,避免了因项数多所带来的不必要的繁琐运算. 例3 (2022年浙江省数学高考第19题第(2)问)如图2,已知四边形ABCD和四边形CDEF都是直角梯形,AB∥DC,DC∥EF,AB=5,DC=3,EF=1,∠BAD=∠CDE=60°,二面角F-DC-B的平面角为60°.设M,N分别为AE,BC的中点,求直线BM与平面ADE所成角的正弦值. 图2 2022年浙江高考19题图 图3 补形图 分析本题的几何体是一个五面体,多数学生使用向量坐标法进行处理,此法思路比较简单,但需要建立空间直角坐标系,并求平面ADE的法向量坐标和直线BM的向量坐标,有一定的运算量.对于运算能力较弱的学生,容易造成失分.此题若用几何综合法进行处理,关键是找平面ADE的垂线所在的位置.由于题目的背景是一个五面体,形状有点“丑”,致使直线BM与平面ADE所成角被“丑”化,若通过补形的方法,过点A作AC1∥CB,AF1∥BF,CF∥C1F1,如图3,将原来的五面体补成一个完美的三棱柱BCF-AC1F1,易证这是一个正三棱柱. 又因AD=DE,M为AE的中点,根据几何体的对称性,易证DM⊥平面ABFE,即平面ADE⊥平面ABFE. 过点B作BH⊥AE,点H为垂足,则BH⊥平面ADE,∠BMH就是直线BM与平面ADE所成角. 在直角梯形ABFE中, 评注在研究不规则的几何体时,几何体的一些重要几何特征被遮掩,导致解题思路受阻.若通过补形方法,将几何体从“非常规形”转化为“常规形”,几何体的性质往往会突显出来,从中可以获得有价值的重要解题信息. 3巧用对称,以一当二 图4 2022年浙江高考第21题图 分析本题涉及重要的点有A,B,C,D,P,Q,其中A,B,C,D是动点.根据条件可知,A与C,B与D分别关于点P“对称”,同时,A与C之间的关系和B与D之间的关系又具有类同性. 评注一个数学问题中的所有信息都是一个有机整体,它们之间有千丝万缕的联系,而各部分信息之间的精彩配合往往是解题成功的必要前提,因此解题时要从整体的视角去审视问题,充分挖掘题目中有价值的信息,并发挥这些信息在解题中的作用,这样常常收到事半功倍之功效. (注:e=2.71828…是自然对数的底数) 由于方程结构比较复杂,要了解这三个根的分布情况,需要转化为函数问题进行处理,设 因为0 又因为x1 所以0 由g(x1)=g(x3)=0,得 ① ② ③ ④ ⑤ 根据⑤式是齐次式的特征,再设 则⑤式又变形为 有大格局的胸怀是一个人的重要品质.因此,在认识数学问题时,要重视从整体上把握题目的条件、结论及数量关系,认清整体与局部之间的关系,把握问题的本质.在解决数学问题时,应注重从数学问题的整体形式、整体结构、整体特征上进行处理.2 会用补形,化丑为美









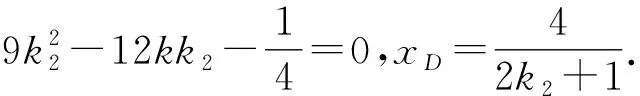





4 活用代换,化难为易