2019年高考数学浙江卷压轴题的自然解法
2023-08-30 07:14甘志国
数理化解题研究 2023年22期
甘志国
(北京丰台二中,北京 100071)
文章针对2019年高考数学浙江卷第22题压轴题给出多种自然解法.
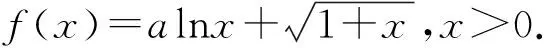
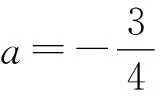
注:e=2.718 28…为自然对数的底数.
分析在第(1)问中,参数a变成了常数-3/4,因而难度不大,只是在根式求导、恒等变形上有些计算量.

可尝试着用减元法来证明这个二元条件不等式成立.

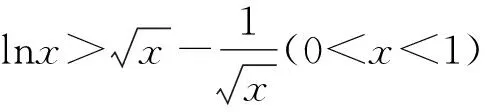
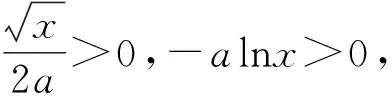


①


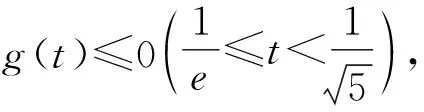

故h(t)单调递增.
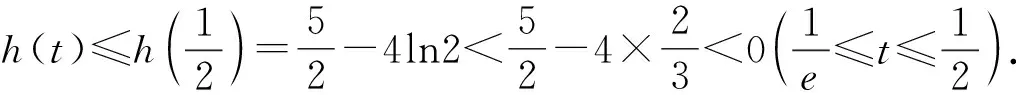


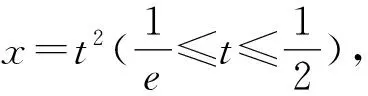
4tlnt+t2+1≤0
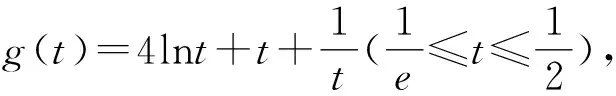

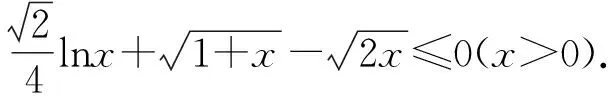
②
下面用四种方法证明该结论成立.
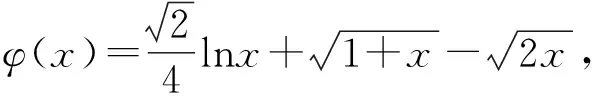
进而可得
下证当0



再由恒等式4x3+8x2+5x-1=(2x+1)(2x2+3x-1)+4x,可得欲证结论成立.
再证当x>1时,φ′(x)<0,即证
4x4+4x3-3x2-6x+1<0,
即证(x-1)(4x3+8x2+5x-1)<0,
即证4x3+8x2+4x+(x-1)>0.
进而可得欲证结论成立.
所以φ(x)在(0,1),(1,+∞)上分别单调递增、单调递减.再由φ(1)=0,可得不等式②成立.


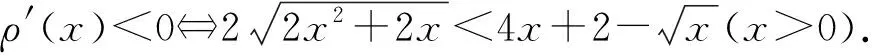

再由恒等式8t4-8t3+9t2-4t+4=2t2[(2t-1)2+3]+(t-2)2,可得ρ′(x)<0,ρ(x)单调递减.又由ρ(1)=0,可得φ(x)在(0,1),(1+∞)上分别单调递增、单调递减.再由φ(1)=0,可得不等式②成立.
解法3在不等式②中可设x=t4(x>0),得
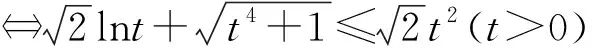

因而不等式②成立.

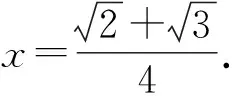

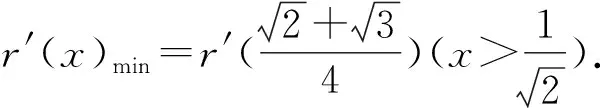

所以r(x)单调递增,得
③


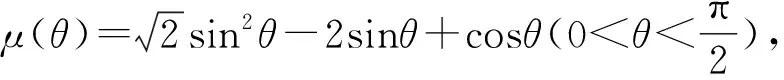

④
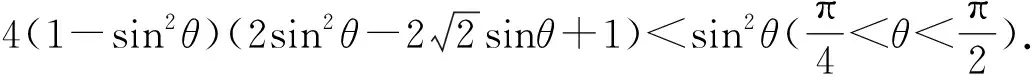


小结在高考导数题中,求参数取值范围时,常常用特殊值试探出一个必要条件(即得到参数的一个取值范围;对于难一点的问题,有时要多取几次特殊值,得到参数的最小取值范围,即求交集),再想办法证明该必要条件也是充分条件(往往是要证明一个条件不等式成立).如果是多元不等式,往往需要减元,减元的方法有主元法、均值不等式法、分类讨论法、换元法(有时用三角换元法还可把无理式化成有理式)等.
猜你喜欢
中学生数理化(高中版.高二数学)(2022年6期)2022-06-30
中学生数理化(高中版.高二数学)(2022年6期)2022-06-30
民族文汇(2022年23期)2022-06-10
中学生数理化(高中版.高二数学)(2021年4期)2021-07-20
河北理科教学研究(2020年3期)2021-01-04
数学物理学报(2019年4期)2019-10-10
中学数学杂志(初中版)(2019年4期)2019-09-18
重型机械(2019年3期)2019-08-27
周口师范学院学报(2018年5期)2018-09-28
发明与创新·中学生(2016年3期)2016-03-29

