小回线瞬变电磁探测线圈的耦合影响因素分析

万 玲，高 升，林小雪，王华梁

（吉林大学a.仪器科学与电气工程学院；b.地球信息探测仪器教育部重点实验室，长春 130026）

0 引 言

近年来，小回线瞬变电磁法已经越来越多地应用在城市工程勘查、隧道探测、水文地质和未爆物探测等方面［1］。小回线瞬变电磁系统适用于浅层地质信息的探测，具有可移动性强、横向分辨率高、可在狭小空间内探测等优点［2］。但是这种系统的接收线圈尺寸较小，通常需要增加线圈的匝数达到增加等效接收面积的目的［3］。匝数的增加不仅会增大线圈本身的自感，还会使线圈之间的互感急剧增加。这意味着发射线圈和接收线圈之间的耦合现象更加严重，使浅层探测盲区增大［4］。因此需要分析线圈的关键参数对自感和互感的影响，从而设计出低自感的接收线圈和弱耦合的瞬变电磁探测系统，以改善接收信号的质量。

针对瞬变电磁探测系统中线圈的耦合问题，已有众多学者从线圈结构和后期数据处理两方面提出了解决思路。嵇艳鞠［5］研究了一次感应电压及其过渡过程对全程瞬变响应的影响，论证了剔除一次场的过渡过程可以获取全程瞬变二次场，并开发了一套ATTEM数据处理及解释软件，其处理效果主要与理论值的计算精度有关。Auken等［6］采用回线偏移的方式研制了tTEM系统，可用于在平坦地形下进行高效率地浅层地质探测，但该系统长度达14 m以上。以上研究虽然可以在一定程度上解决一次场耦合问题，但并未详细地从原理上对小回线瞬变电磁的耦合机制进行分析，在弱耦合线圈参数设计方面缺乏全面的理论指导信息，因而还需要对线圈互感的影响因素做更深入的研究。

本文使用电磁场仿真软件构建不同参数、不同相对位置的接收线圈模型，通过分析多种关键参数对接收线圈自感和互感的影响，探索不同参数对接收线圈的影响规律，完善线圈的弱耦合设计方案，从而避免复杂的线圈补偿结构或后期数据处理，同时可以优化接收线圈的自感情况，为实现小回线瞬变电磁系统实现弱耦合提供技术基础。

1 小回线瞬变电磁法工作原理

瞬变电磁法的工作原理如图1 所示，发射机的激发电流一般为矩形、半正弦形、梯形、三角形、伪随机等波形［7］，仿真分析中以矩形波为例。装置工作时向发射线圈中通入阶跃电流i1，根据电磁感应理论，变化的电流会产生磁场，该发射线圈产生的磁场称为一次磁场。该磁场在传播过程中，如果遇到地下的异常体，将在异常体内部激发感应电流i2。i2的变化又会产生新的磁场，称为二次磁场。该新磁场的变化会使接收线圈中产生感应电压，即二次感应电压［8］，其中包含了异常体电阻率和分布位置等相关信息。

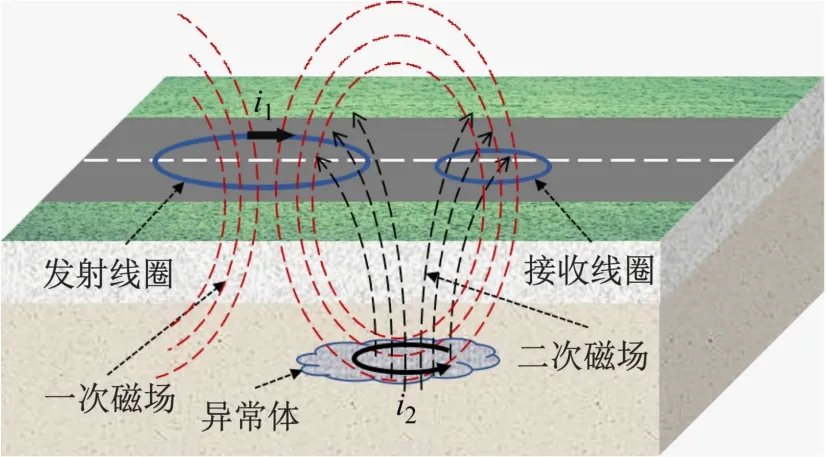
图1 小回线瞬变电磁法原理图

显然，接收线圈在接收到二次磁场的同时也会直接捕获一次磁场的变化，产生一次感应电压［9］。发射电流初始值为I1，电流关断时间为t0，发射线圈与接收线圈之间的互感系数为M，接收线圈中一次场感应电压为u1（t），则

二次感应电压是异常体的感应涡流变化使接收线圈产生的感应电压。异常体可以等效为一个单匝电流环，假设等效电流环的电感为L，电阻为R，时间常数τ＝L／R，发射线圈与电流环的互感系数为M2，等效电流环与接收线圈的互感系数为M3，接收线圈的二次感应电压为u2（t），则

瞬变电磁法所探测的地质信息包含在二次感应电压中，而接收线圈直接耦合到的一次感应电压不仅没有包含地质信息，还会使二次感应电压产生畸变，即接收线圈的过渡过程，影响探测的深度与精度。因此在瞬变电磁探测系统中，发射和接收线圈之间的耦合应尽可能为零。

2 自感、互感的计算

在小回线瞬变电磁系统中，接收、发射线圈的形状一般以圆形、方形为主。综合考虑仿真设计、实际效果等因素，仿真中采用发射线圈和接收线圈均为圆形的方案。

2.1 自感计算

在制作发射线圈和接收线圈时，应尽可能使自感降低。降低发射线圈的自感可以有效减少关断时间，使发射波形尽可能实现理想关断。降低接收线圈的自感则可以增大线圈的带宽，获得更完整的二次场信号，并且可以改善线圈的过渡过程，减小浅层探测盲区。

杨海燕等［10］给出了单匝和多匝圆形线圈电感系数的计算方法，单匝圆形线圈的自感为

多匝线圈是由单匝线圈串联而成，即多个自感串联，可以等效成1 个自感。且每匝线圈的参数均相同，故每匝回线的自感系数及任意两匝回线间的系数都相等，则多匝圆形线圈的自感为

式中：N为匝数；μ0为真空磁导率；RS为接收线圈的半径；r为接收线圈的导线半径。由式（4）可见，线圈的自感由N、RS和r决定，不过该计算公式是忽略绝缘层厚度影响的一种近似算法。

2.2 互感计算

如上所述，接收线圈感应到一次电压的大小由M、I1和t0决定，其中I1由探测需求决定，t0由发射系统决定。故若要消除一次场及过渡过程的影响，就必须使收发线圈之间的M尽可能为零。线圈之间互感的计算比较复杂，因此，能快速准确地计算出互感对解决该问题有很大的帮助。但互感的计算方法并不唯一［11］，文献［12-14］中比较详细地总结了平行线圈的互感计算问题。

本文采用Grover等［15］提出的方法，简单阐述具有平行非共轴的圆形线圈之间互感的计算，如图2 所示为平行非共轴线圈布设示意图，其中：RP为发射线圈的半径；c为2 个线圈间的轴向距离；l为径向距离；Ø是半径为RS的次级线圈任意点的积分角；K（k）是第1类椭圆积分；E（k）是第2 类椭圆积分；μ0为真空磁导率，μ0＝4π ×0.1 μH／m。需要注意的是，RP需大于RS，且c≠0，RS≠l，否则会出现奇异值。则2 个线圈之间的互感为：

图2 平行非共轴线圈布设示意图

实际上，线圈之间的互感除了主要受到线圈的半径、轴向距离、径向距离等因素的影响外，还会受到导线半径、导线间距、缠绕方式等多种因素的影响。因此，需要对不同的因素分别进行研究，了解这些因素对互感的影响效果，从而确定接收线圈的设计和线圈相对位置。

3 线圈关键参数对自感、互感的影响

本文使用COMSOL 软件对不同参数的接收回路进行建模，通过参数扫描的方式得出不同情况下接收、发射之间的互感值，进而分析各种参数对互感的影响效果，同时进行自感的扫描。在本文所有模型中，发射线圈和接收线圈全部为均匀多匝的圆形线圈。二者Y轴距离（径向距离）默认为0 m，Z轴距离（轴向距离）默认为0.5 m，发射电流为10 A。接收线圈的横截面如图3 所示，其中：RS＝0.5 m，接收线圈导线半径r＝0.4 mm，导线间距D＝0.5 mm。

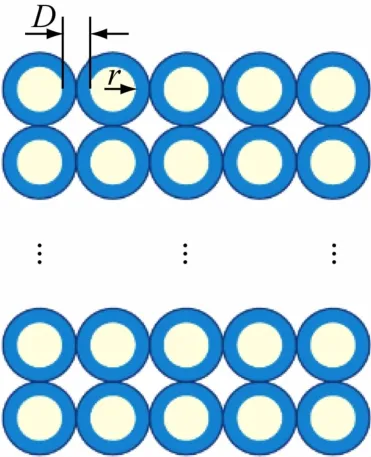
图3 接收线圈横截面示意图

3.1 r和D的影响

当r选用不同尺寸时，其产生的M和L幅度变化情况分别如图4 和5 所示。其中，参数r的范围为0.1～2.0 mm。

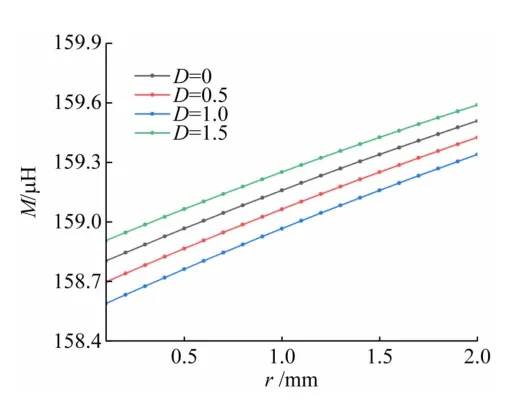
图4 M随r的变化情况

图5 L随r的变化情况

由图4 和5 可知，线圈之间的M与r近似呈线性关系，且随着r的增大而增大，但是增大的速度会逐渐变缓。当r由0.4 mm变为0.5 mm时，线圈之间的m值增加约40 nH，此时接收线圈感应电压的峰值增加约88 μV，接收线圈的L值会降低约221 μH，若忽视分布电容变化的影响，线圈的谐振频率会从332 kHz提升至337 kHz。由此可见M受r的影响较小，但接收线圈的L受r的影响较大。

实际导线外部会有绝缘层，将两个绝缘层的厚度之和视作导线表面之间的距离，即导线表面距离D，当选用不同厚度的绝缘层时，其产生的M和L幅度变化情况分别如图6 和图7 所示。其中，参数D的范围为0～2.0 mm。由图可知，D对M、L的影响与r对其影响类似。M随着D的增大而增大，L随着D的增大而减小。当D由0.4 mm变为0.5 mm，线圈之间的M值会增加约20 nH，接收线圈感应电压的峰值增加约42 μV，而L会减少约120 μH。

图6 M随D的变化情况

图7 L随D的变化情况

M会随着r和D的增大而增大，但变化的幅度很小，仅为nH级别。L受二者的影响很大，且随着二者的增大而减小。选取合适的r和绝缘皮厚度可以在几乎不增加M的同时大大降低L，这可以有效提高接收线圈的谐振频率，提高二次场信号的完整性，从而提高浅层目标体的探测能力。

3.2 N和RS 的影响

当N、RS同时改变时，M、L的变化情况如图8 和图9 所示。其中，RS＝0.05～1.00 m，N＝5～100匝。图中黑色的2 条线分别是100 μH和10 mH的等值线。由图8 和9 可知，与r或D不同，N、RS对M和L的影响非常大。无论是N的增加还是RS的增大，都会导致M和L的急剧上升。例如RS＝0.2 m，N＝40匝时，M≈20.84 μH，L≈1.69 mH，此时接收线圈中的感应电压峰值为0.41 V。若将RS增加为0.4 m，N增加为80 匝，M会提升至163.19 μH，L提升至14.09 mH，感应电压峰值增大到3.21 V。

图8 M随RS、N的变化情况

图9 L随RS、N的变化情况

可以看出，N和RS的变化对一次感应电压的影响十分明显，故N、RS均不能太大，否则会导致M过大，进而使接收线圈耦合到的一次感应电压过于强烈，甚至会直接使接收机饱和。此外，L太大会影响过渡过程，降低接收线圈的带宽［16］。

3.3 收发线圈不同相对位置的影响

当接收线圈与发射线圈的相对位置改变时，结果如图10 所示。其中，l＝ 0～ 5.0 m，c＝ 0～1.5 m。

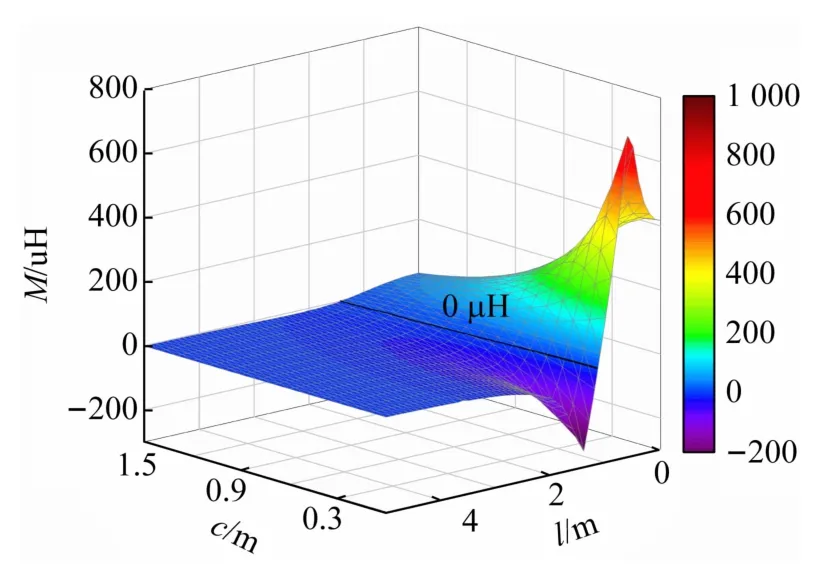
图10 M与相对位置的关系

由图10 可知，M与相对位置的对应关系并非简单的单调性变化。当c＝0 m，l＝0.6 m 时，M达到最大，为704.60 μH。c＝0 m，l＝1.4 m时，M出现另1 个峰值，绝对值为248.88 μH。即使2 个线圈距离较近，理论上也存在无限多处可以实现零耦合的位置，但是对两个线圈的相对位置精确度要求较高，还需要固定不变，这在现实中是比较难实现的，因为2 个线圈比较近时，几厘米的位置变化也会引起互感的剧烈起伏。例如c＝0 m，l＝0.4 m时，M＝556.85 μH，但当l＝0.5 m时，M会升至666.89 μH。而当c和l较大，例如当l＝4.5～5.0 m 时，M的绝对值会稳定在2 μH以下，此时一次感应电压峰值只有几十mV。

4 结 语

本文通过构建不同的探测线圈模型，研究并分析关键参数对发射、探测线圈之间的耦合效果和自感的影响规律。结果发现，在选择探测线圈的导线半径和绝缘层厚度时，可忽略对互感的影响，适当增大导线半径和绝缘层厚度，这样可以有效降低线圈的自感；在设计接收线圈的半径和匝数时，应该在满足等效接收面积的前提下尽量减小线圈的半径、减少线圈的匝数，从而使线圈的自感和耦合效果显著减小；在设计收发线圈的相对位置时，可以选择零耦合等值线上的点或者直接增大径向距离。本文可应用于小回线瞬变电磁法的弱耦合设计和优化接收线圈的自感情况。