旋转水槽颗粒流试验的流体形态

倪龙良，梁 龙，邓检良

（1.上海交通大学船舶海洋与建筑工程学院，上海 200240；2.浙江省工程勘察设计院集团有限公司，浙江宁波 315012）

0 引 言

泥石流对生命财产和生态环境等造成了严重危害，主要形式为破坏河道，也包括侵袭公路、铁路等交通线路，例如2022 年贵州榕江站动车脱线事故就由泥石流侵袭动车路轨引发。因此，国内外学者对泥石流的运动机理展开了系统的研究，取得了一系列成果，文献［1-2］中以Savage-Hunter（SH）模型［1］为理论基础，以大型泥石流试验结果为实验基础，建立了基于深度平均法的泥石流理论体系。在SH 模型中，假设沟底与颗粒流之间的摩擦服从库仑摩擦定律，同时假设横截面上的纵向压力可以采用底压与土压力系数的乘积确定。SH 模型及其扩展形式已被许多水槽试验［2-4］和野外观测记录证实［5］。Iverson［6］对沿粗糙河床稳定移动的理想化泥石流混合物进行分析，证实该模型可以预测实验泥石流的速度和深度。另一方面，很多研究者提出对土压力系数进行了改进，例如采用Rankine 公式的改进方法［7-8］；或者将土体压力作为各向同性处理，从而直接将土压力系数取为1［9-10］。

试验研究方面，近年采用了旋转水槽的方法再现泥石流取得了进展［11-13］，该方法的特征是用水槽的旋转模拟无限长斜面，并使流体形成稳定的流动［14］。由于颗粒流（包括泥石流）流动问题的复杂性，目前尚无出现采用SH模型及其扩展形式对旋转水槽颗粒流试验稳定流动的模拟计算，这导致人们对旋转水槽试验结果的有效性产生怀疑。

本文以Savage-Hunter（SH）模型为基础，通过修正土压力系数及考虑沟底倾斜角变化和离心力影响建立旋转水槽颗粒流流体的二维流动模型；同时用数值计算和试验研究对比，重点分析旋转水槽试验的颗粒流深度、长度及龙头龙尾位置变化等规律，验证该模型和数值计算用于分析旋转水槽颗粒流试验的流体形态变化规律的有效性。

1 改进的Savage-Hunter模型

在旋转水槽试验中的颗粒流流体形态有特殊性：在稳定流动状态下，其平均绝对速度为零；颗粒流长度与旋转水槽转速有关。为研究这一流动特性，采用SH模型并假设：11 忽略垂直于床层的速度分量，且运动过程中的质量和密度保持恒定，不考虑动量扩散效应；22 以深度平均流速代表实际速度，且沟底与颗粒流之间的摩擦角（简称界面摩擦角）与速率无关。

SH模型的基本方程是针对平直的沟底情况而提出的，本文首先将SH 模型推广到静止的圆弧形沟底情况，然后进一步推广到旋转的圆弧形沟底情况。

1.1 静止的圆弧形沟底的SH模型

考虑固体颗粒状材料沿旋转水槽装置的圆弧形底部轮廓的表面流动（见图1），假设颗粒流不可压缩流体，且水槽的旋转速度为零，即圆弧形沟底静止不动。

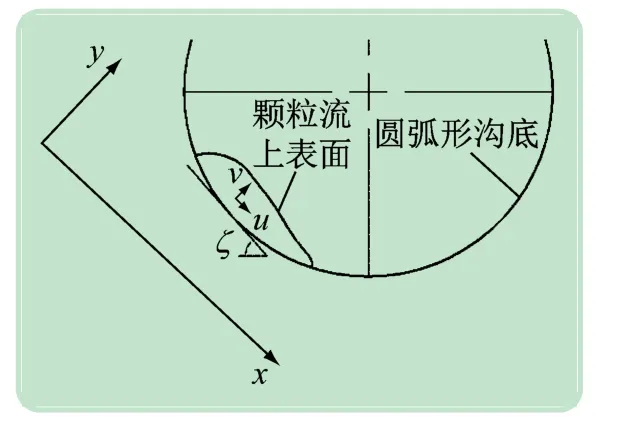
图1 颗粒流沿静止的圆弧形沟底运动

根据SH 模型，考虑沟底的倾角ζ 是随位置发生变化的，并以圆弧形沟底可产生离心力导致沟底正应力加大［5］，可得圆弧形沟底的动量守恒方程和质量守恒方程：

式中：Kact为主动土压力系数；Kpass为被动土压力系数；θ为颗粒的内摩擦角。

由式（1）和（2）组成的偏微分方程组包含未知数深度＾h（x，t）和横向平均速度。如果已知界面摩擦角δ、内摩擦角θ和沟底几何形状b（x），以及初始轮廓和速度分布，则就能确定颗粒流的深度＾h（x，t）和平均速度（x，t）。

1.2 旋转的圆弧形沟底的SH模型

在旋转水槽试验中，圆弧形沟底处于旋转运动，其动量守恒方程与前述静止状态下的圆弧水槽对应的动量守恒方程有两点不同：

式中，uflume为水槽槽底处运动速度。需要说明的是，式（4）中的是平均化的绝对速度，并不是沟底处的绝对速度，而式（4）仅仅用于判断摩擦力方向，对稳定流动状态下的计算影响不大。

（2）土压力系数的取值不同。旋转水槽试验结果表明，在水槽旋转速度不高的条件下，颗粒流流动状态以层流状态为主，层面与沟底底面大致平行［15］。因此，可认为颗粒流内部发生塑性流动时的剪切破坏面与沟底底面大致平行。沟底底面方向上的正应力为pyy，该应力大致等于上述剪切破坏面上的应力；相对应地，pxx为与剪切破坏面垂直方向上的正应力，如图2所示。对应的土压力系数

图2 沿着内部破坏的莫尔应力圆和破坏包络线

式（5）和式（3）的主要区别在于对颗粒体内部的破坏面的判断不同。式（3）的依据是固体颗粒在床层发生滑移时的莫尔圆分析结果，并认为这种破坏形式也存在于颗粒流内部。而式（5）是直接依据旋转水槽试验观测结果：无论沟底的界面摩擦角多大，颗粒流内的大部分的剪切破坏面都与沟底底面大致平行，因此采用图2 所示莫尔圆，这个莫尔圆与界面摩擦角δ 无关，且没有主动土压系数和被动土压系数的区别。

依据式（4）和（5），且将控制方程式（1）和（2）的所有变量转换为有量纲形式。得如下控制方程：

2 数值计算及结果

对式（6）采用拉格朗日法［1］求解，将颗粒流切分成一系列的“四边形＋弓形”单元体（见图3），网格单元的边界旋转水槽底边切线垂直。在时间步长为n－1 时的网格边界点定义为xj，n－1，边界点处的速度定义为uj，n－1，单元块的速度ˉui，n－1，边界点对应的颗粒流深度定义为＾hi，n－1，其中下标i对应的是网格单元中心，j对应的是靠近左侧网格i的网格单元边界点j。

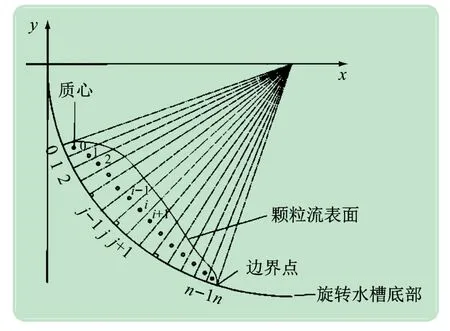
图3 拉格朗日法网格单元符号的定义

假定在初始时刻已知边界点速度uj，n－1、边界点位置xj，n－1、hj，n－1的初始数值，将已知的颗粒块的速度用插值法转换为边界点的速度uj，n－1后，计算经过时间步长dt后得到边界单元点xj，n新位置（式（7）），然后确定单元中心点i上单元体的深度＾hi，n，最后，根据式（6）求解单元块i在n时刻的速度：

偏微分的计算方法同文献［1］。本文数值计算方法与SH模型计算方法最大的不同是在离散单元体中考虑倾角ζ的变化；另外，采用了式（4）和（5）判断摩擦力方向和计算土压力系数，即：

在图3 坐标系下，旋转水槽槽底表达为式（9），设初始时刻颗粒流的上表面为式（10），内摩擦角θ ＝39°，界面摩擦角δ ＝31°，时间步长dt＝2 ms，uflume＝0.06～0.10 m／s。采用数学工具软件Mathcad 15 M050 版本编写程序，求解h、L、u、β 及龙头位置等参数，其中视摩擦角、龙头等的定义如图4 所示。数值模拟与试验测试结果如图5 和6 所示。

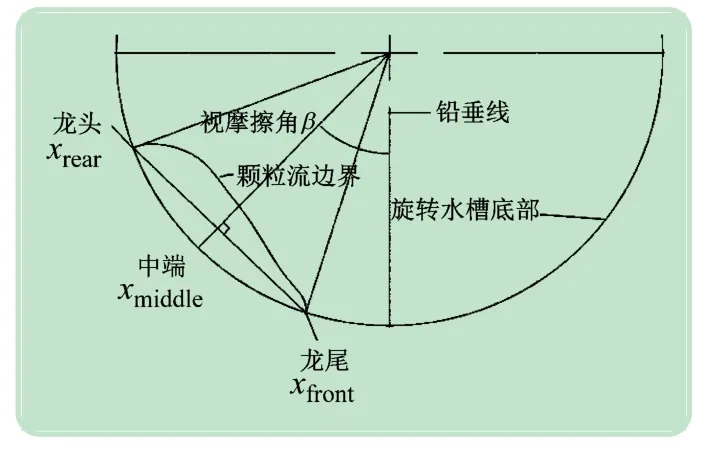
图4 视摩擦角定义

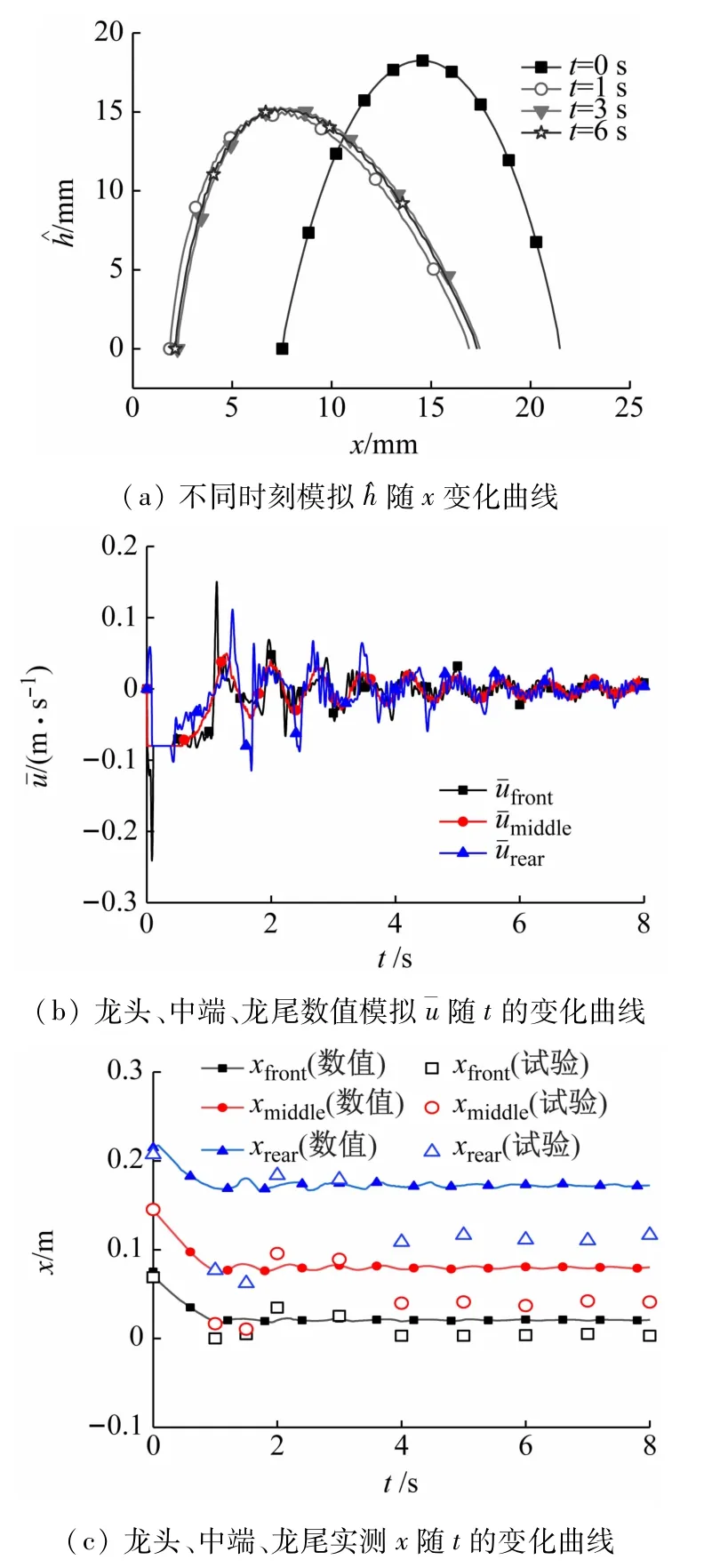
图5 uflume ＝0.08 m／s时颗粒流数值计算和实测结果

3 旋转水槽试验

3.1 试验方法

如图7所示为旋转水槽装置（或称为滚筒试验装置［14］）制备颗粒流。系统由旋转水槽（有机玻璃，内径φ29 cm，槽底宽6 cm）、动力系统（步进电动机和传动装置）、摄影系统（50 f／s）三部分组成。试验装置的特征是水槽的转速由计算机驱动模块精确控制。

试验颗粒材料是硅砂（密度2.65 g／cm3；50 μm孔径硅砂）。采用动态试验方法测量［16］，测得θ ＝39°，硅砂与有机玻璃之间δ ＝31°。

试验初始状态及旋转水槽初始速度与数值计算的输入初始状态一致。水槽旋转一段时间后，颗粒流会达到稳定状态。在后处理阶段，采用AE 软件根据摄影记录，提取颗粒流的位置坐标，每秒取5 点。需要说明的是，为保证流动的稳定，旋转水槽速度uflume设定在0.06～0.1 m／s之间。

3.2 试验结果与数值计算结果的比较

由于旋转水槽试验自身的特殊性，在水槽旋转一段时间后，可以观测到颗粒流稳定的流动状态（见图7（b））。在此状态下，ˉu（x，t）≈0（见图5（b）），这一现象表现为稳定流动状态下的β 稳定不变。由图6（a）可知，在不同的旋转速度条件下，试验测定的β与旋转速度无关，为30°；计算得到的β 也与旋转速度无关，为28°。计算结果与试验结果接近，结果表明：＾h（x）在不同时刻存在一定差异［见图5（a）］，但是差异很小，最大差异仅仅3 mm；而颗粒流上表面局部的小波动就超过1 mm［见图7（b）］；颗粒流龙头、中端和龙尾位置随时间变化明显［见图5（c）］，这导致对深度＾h（x，t）的直接的测量和试验验证存在一定的困难。另一方面，在颗粒流体积不变的条件下，L（t）的变化可以大致反应＾h（x）最大值＾hmax的变化，因此，由图6（b）中L（t）的实测值和计算值表明，L（t）在稳定流动状态下，实测值和计算值分别为150 和165 mm，二者相差10%，属于可接受的误差范围内。

图6 颗粒流数值计算与实测变化曲线

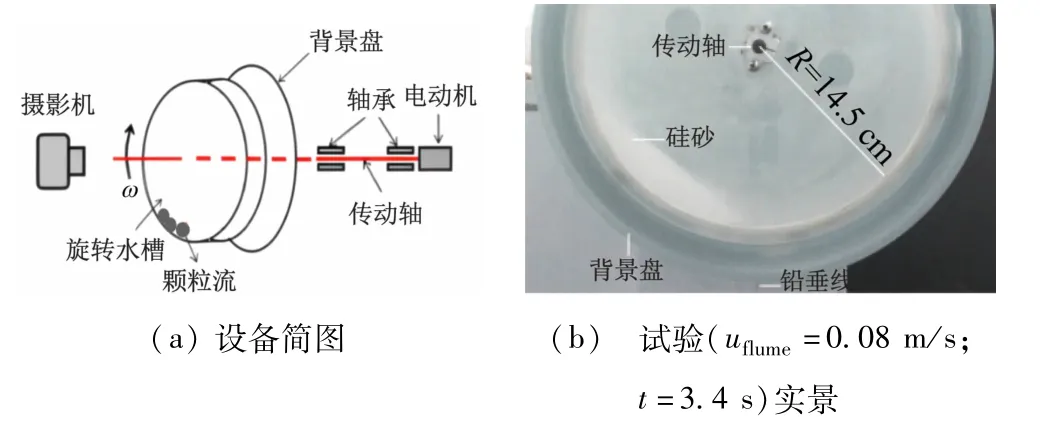
图7 旋转水槽试验

4 结 语

本文在Savage-Hunter（SH）模型基础上研究旋转水槽试验中的颗粒流流动特性，建立了流体形态计算模型及相应数值计算方法，并进行数值计算与试验结果对比分析，结果表明：

（1）考虑到颗粒流的流动特性，应对SH 模型中的土压力系数进行修正。水槽旋转速度不高的条件下，颗粒流流动状态以层流状态为主，层面与沟底底面大致平行，可以认为颗粒体（硅砂体）发生塑性流动时的剪切破坏面与沟底底面大致平行。因此土压力系数须做相应修正。

（2）计算与试验结果一致，颗粒流最终进入稳定流动状态。稳定流动状态下，视摩擦角的实测值和计算值分别为30°和28°；流体直线长度的实测值和计算值分别为150 mm 和165 mm。实测值和计算值相差不大。修正后的计算模型［式（6）］和相关的数值计算方法可用于研究旋转水槽试验中的硅砂颗粒流流体形态。

本文的研究为旋转水槽试验在泥石流试验研究领域的进一步发展提供理论依据和数据支撑。但对于水槽旋转速度对颗粒流运动特征的影响，缺少更多的试验结果，尚需进一步研究积累水槽旋转速度对颗粒流流体形态的影响。