考虑土拱效应的铁路刚性挡墙主动土压力计算方法
路维,孙文君,王学民,杨鹏志,崔立功
(河北工程技术高等专科学校,河北沧州061001)
考虑土拱效应的铁路刚性挡墙主动土压力计算方法
路维,孙文君,王学民,杨鹏志,崔立功
(河北工程技术高等专科学校,河北沧州061001)
对考虑土拱效应的水平微元滑裂体水平向及竖向静力平衡方程进行了分析,获得了平移模式下的刚性挡土墙侧向主动土压力、主动土压力合力及其作用点的计算公式,并与模型试验数据进行了比较。结果表明:本文得到的平移模式下刚性挡土墙墙后主动土压力分布与模型试验结果吻合较好,最大值比实测值略大;墙背主动土压力沿墙高呈非线性分布,墙背主动土压力合力作用点高度大于墙高的1/3。
土拱效应;刚性挡土墙;主动土压力分布;应力莫尔圆
目前铁路挡墙设计的墙背土压力计算均采用库仑等经典土压力理论,但经典理论的墙背土压力分布是线性的,这与试验测得的非线性分布不符[1]。这是因为经典土压力理论没有考虑土拱效应。土拱效应导致了墙背土压力呈线性分布[1],文献[2-8]对平移模式下刚性挡土墙墙背主动和被动土压力的分析中考虑了土拱效应,得到的墙背侧向主动土压力分布与模型试验[9-10]结果较一致。文献[2-4,7]在墙背侧向土压力分析中采用了朗肯滑裂面,而文献[5-6]采用了库仑滑裂面。朗肯土压力理论比库仑土压力理论严密[11]。文献[3-4]采用土拱效应较好地分析了墙背侧向主动土压力,但微元滑裂体的受力平衡推导中有误,误认为滑裂体的水平向力自动满足平衡,以及误认为滑裂面上的力在竖向上的投影为0。
本文在文献[3-4]的基础上,纠正其中的失误,推导出合理的墙背侧向土压力及其系数、墙背侧向主动土压力合力及其作用点高度的计算公式。
1 主动土压力分析
1.1受力模型
研究对象与文献[3-4]相同,为平移模式下处在主动极限状态下的墙面垂直、墙填土表面水平的刚性挡土墙。主动极限状态下的墙后砂性土体破裂面采用朗肯破裂面,滑裂面倾角=45°+φ/2,φ为填土内摩擦角。假定滑裂土体的小主应力迹线为圆弧曲线[2-3],见图1。滑裂体内部土体的应力莫尔圆见图2。
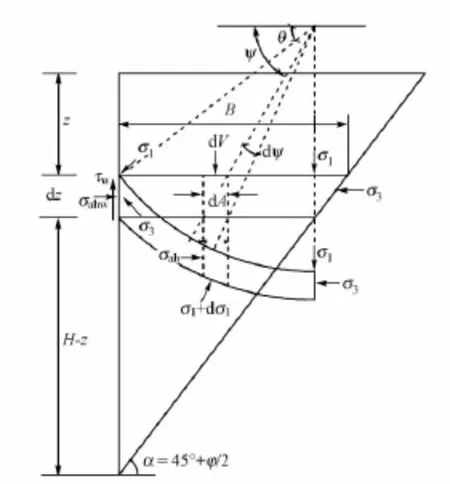
图1 微元滑裂体小主应力迹线
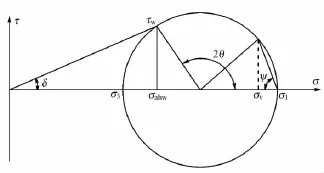
图2 滑裂体内土体应力莫尔圆
1.2土应力分析
根据图2,可得微元滑裂体内任意点水平平面上的竖向应力σv为

式中:

同理,可得微元滑裂体墙面处的水平应力σahw、剪应力w、主应力偏转角θ分别为[7]
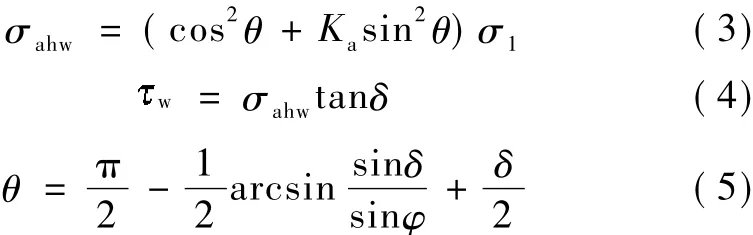
式中,δ为墙土摩擦角。
1.3侧向主动土压力系数
假定滑裂体中小主应力迹线为圆弧线,则可得σahw与微元滑裂体水平面上的平均竖向应力σav的关系,即主动土压力系数Kawn为[3,8]

1.4侧向主动土压力
取墙顶以下任意深度z处的微元滑裂体进行受力分析,如图3所示。
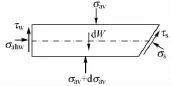
图3 微元滑裂体受力模型
由微元滑裂体水平方向的静力平衡,可得

对于微元滑裂体竖向的静力平衡方程,在文献[3-4]中认为滑裂面应力在竖向上的分力为0,但这属误解。微元滑裂体竖向静力平衡的正确方程为

式中:γ为填土的重度;z为微元滑裂体距填土面的距离;H为墙高;B为微元滑裂体的宽度。
文献[3-4]误认为dBσav=Bdσav,而实际上dBσav=Bdσav+σavdB。
由图1可知

则

把式(4),式(6),式(7),式(9)和式(10)代入式(8),可得微元滑裂体水平面上平均竖向应力的微分方程为

式中,λ为系数,其表达式为
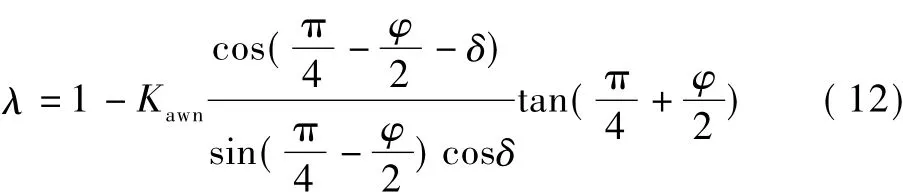
根据边界条件σavz=0=q(q为填土表面荷载)对上式积分,并由式(6)可得墙背侧向主动土压力

将式(13)对z积分,可得倾斜墙背法向主动土压力合力Eaw为

将式(13)按下式积分,可得墙背侧向主动土压力合力相对于墙趾的弯矩M为
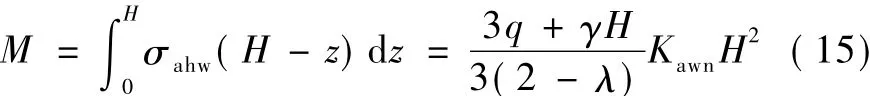
由式(14)和式(15),可得墙背侧向主动土压力合力的作用点高度h为
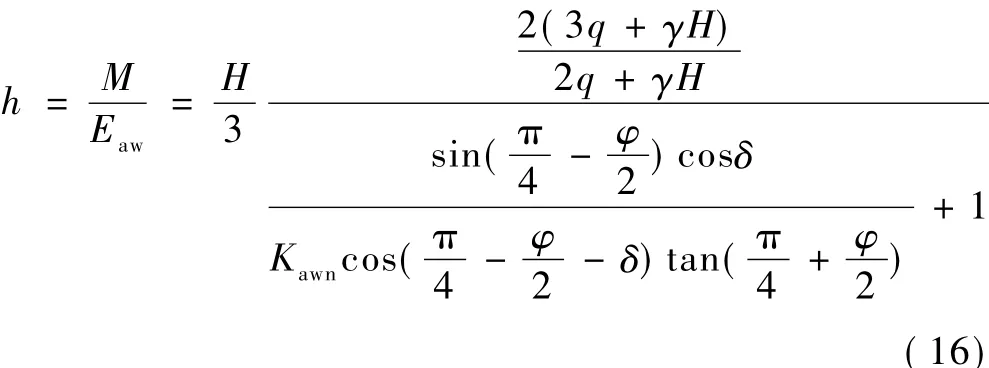
2 公式验证
本文推导的墙背侧向主动土压力计算公式计算值与实测值对比见图4。其中模型试验结果取自文献[8],计算参数均同文献[9]:墙高H=1m,填土内摩擦角φ=34°,填土重度γ=15.4kN/m3,墙土摩擦角δ=17°,填土表面荷载q=0。由图4可知,本文方法得到的墙背侧向主动土压力沿墙高的分布与试验结果吻合得较好,且最大主动土压力值比实测值略大。这说明本文推导的公式可以作为挡土墙设计的主动土压力计算公式。
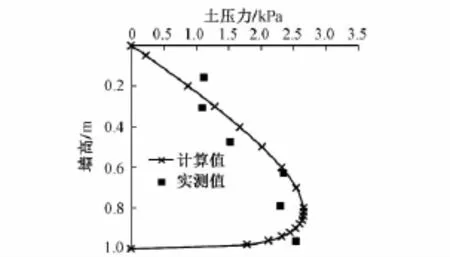
图4 墙背侧向主动土压力公式计算值与实测值对比
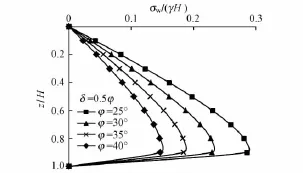
图5 侧向主动土压力随填土内摩擦角的变化规律
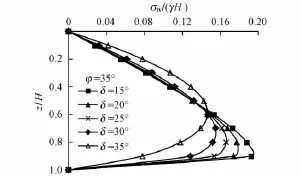
图6 侧向主动土压力随墙土摩擦角的变化规律

表1 墙背侧向主动土压力合力作用点相对高度随填土内摩擦角和墙土摩擦角的变化
3 结果讨论与分析
侧向主动土压力随填土内摩擦角的变化规律如图5所示,随墙土摩擦角的变化规律如图6所示。可见,本文方法得到的墙背侧向主动土压力沿墙高呈非线性分布,随填土内摩擦角的增加而增加,在墙上部随墙土摩擦角的增加而增加,在墙下部随墙土摩擦角的增加而减小;墙背最大侧向主动土压力随填土内摩擦角的增加而增加,随墙土摩擦角的增加而减小。从图5、图6中还可以看出:墙背侧向主动土压力合力随填土内摩擦角的增加而增加,随墙土摩擦角的增加而减小;墙背侧向主动土压力合力作用点高度随填土内摩擦角的增加而有所增加,随墙土摩擦角的增加而明显增加。
墙背侧向主动土压力合力作用点相对高度随填土内摩擦角和墙土摩擦角的变化见表1,随填土内摩擦角和δ/φ的变化见表2。可知:墙背侧向主动土压力合力作用点高度介于0.3333~0.4771倍墙高,随填土内摩擦角的增加而增加,随墙土摩擦角的增加而增加;墙土摩擦角一定时随填土内摩擦角的增加而减小;墙土摩擦角与填土内摩擦角比值一定且<2/3时随填土内摩擦角的增加而增加,但不明显;墙土摩擦角与填土内摩擦角比值一定且>2/3时随填土内摩擦角的增加而较明显地增加。

表2 墙背侧向主动土压力合力作用点相对高度随填土内摩擦角和δ/φ的变化
4 结论
本文对微元滑裂体的横竖向静力平衡进行了分析,并根据土拱效应分析得到平移模式下刚性挡土墙墙背侧向主动土压力分布、土压力合力及其作用点的理论解。结论如下:
1)墙背侧向主动土压力沿墙高呈非线性分布,随填土内摩擦角的增加而增加,在墙上部随墙土摩擦角的增加而增加,在墙下部随墙土摩擦角的增加而减小;墙背最大侧向主动土压力随填土内摩擦角的增加而增加,随墙土摩擦角的增加而减小。
2)墙背侧向主动土压力合力作用点高度介于0.3333~0.4771倍墙高,随填土内摩擦角的增加而增加,随墙土摩擦角的增加而增加,墙土摩擦角一定时随填土内摩擦角的增加而减小,墙土摩擦角与填土摩擦角比值一定时随填土内摩擦角的增加而增加。
[1]顾慰慈.挡土墙土压力计算手册[M].北京:中国建材工业出版社,2005.
[2]HANDY R L.The Arch in Soil Arching[J].Journal of Geotechnical Engineering,1985,111(3):302-318.
[3]PAIK K H,SALGADO R.Estimation of Active Earth Pressure Against Rigid Retaining Walls Considering Arching Effects[J].Geotechnique,2003,53(7):643-653.
[4]GOEL S,PATRA N R.Effect of Arching on Active Earth Pressures for Rigid Retaining Walls Considering Translation Mode[J].International Journal of Geomechanics,2008,8(2):123-133.
[5]李永刚,白鸿莉.垂直墙背挡土墙土压力分布研究[J].水利学报,2003,34(2):102-106.
[6]应宏伟,蒋波,谢康和.考虑土拱效应的挡土墙主动土压力分布[J].岩土工程学报,2007,29(5):717-722.
[7]吴明,彭建兵,徐平,等.考虑土拱效应的挡墙后土压力研究[J].工程力学,2011,28(11):89-96.
[8]俞缙,周亦涛,蔡燕燕,等.基于土拱效应的刚性挡墙墙后主动土压力[J].岩土工程学报,2013,35(12):2306-2310.
[9]YUNG Shoufang,ISHIBASHI I.Static Earth Pressure with Various Wall Movements[J].Journal of Geotechnical Engineering,1986,112(3):317-333.
[10]TSAGARELI Z V.Experimental Investigation of the Pressure of a Loose Medium on Retaining Walls with a Vertical Back Face and Horizontal Backfill Surface[J].Journal of Soil Mechanics and Foundation Engineering,ASCE,1965,91(4),197-200.
[11]刘成宇.土力学[M].2版.北京:中国铁道出版社,2001.
AbstractT his paper analyses the horizontal and vertical static equilibrium equations of horizontal differential sliding mass with soil arch.New formulas of rigid retaining wall lateral active earth pressure,active earth pressure resultant force and its action position were derived under translation mode.T he Comparisons between the theoretical and measured values shown that the lateral active earth pressure distribution of rigid retaining wall under translation mode from the proposed formulas are agree well with results from the model test,and the maximum value from calculation is slightly larger than measured value.T he distribution of the lateral active earth pressure is nonlinear along the wall height,and the action position of active earth pressure is larger than one third of the wall height.
Calculation Method of Active Earth Pressure of Railway Rigid Retaining Wall Considering Soil Arch Effect
LU Wei,SUN Wenjun,WANG Xuemin,YANG Pengzhi,CUI Ligong
Hebei Engineering and Technical College,Cangzhou Hebei 061001,China)
Soil arch effect;Rigid retaining wall;Distribution of active earth pressure;Mohr's stress circle
U213.1+52.2
A
10.3969/j.issn.1003-1995.2016.04.25
1003-1995(2016)04-0098-05
(责任审编李付军)
2015-10-23;
2015-12-11
河北省高等学校科学技术研究指导项目(Z2015191)
路维(1983—),女,讲师,硕士。

