大型接地系统接地阻抗测量的引线互感分析

张宣， 潘卓洪， 何智强， 任章鳌， 李欣

(1.华北电力大学， 河北 保定071003；2.国网湖南省电力有限公司， 湖南 长沙410004；3.国网湖南省电力有限公司电力科学研究院， 湖南 长沙410007)

0 引言

尽管国内外对电力系统接地设计有着不同的要求[1-2]， 但接地测量都是接地工程竣工验收的最终环节。 接地系统接地阻抗测量的准确与否关系到接地工程能否如期投运[3]， 以及接地工程在日后的运行和维护当中能否发挥防雷接地、 防静电接地、安全接地和工作接地等重要作用[4]。 大型接地系统接地阻抗测量目前存在多个难点， 如分流测量不准确[5]、 电源容量不足和测量仪器信噪比不高，以及电压引线和电流引线的互感问题[6-9]。

接地阻抗的测量标准布线方式有两种， 一种是平行布线法(又细分为5D-0.618 法[2，10]和反向布线法[10])， 另外一种是夹角法(2D-30 度夹角法或其他形式夹角法[2])。 在大型接地系统接地阻抗测量时需要布置长距离的电压和电流引线， 互感对接地阻抗的测量结果有重要影响。 以文献[9] 的某大型接地工程为例， 现场实测结果表明在平行布线引线间距离为4.5 m 的情况下， 引线间互感达到了0.4 Ω/km。

国内学者一直致力于接地测量互感问题的研究。 解广润和方瑜等人提出在站址附近引入一个辅助电极来消除引线间互感， 但未见推广应用[11-12]。李汝彪等人用附加串联电阻来消除互感影响， 但该法不适用于大型接地系统[13]。 端木林楠等人提出了“双频-双路径电压线布置” 的互感校正方法，但工作量较大[14]。 黄新波和侯苏洋等人提出了使用平行互感公式来校正接地测量结果[6，8]。 马御棠等人提出了二次直线测量法消除互感， 但未见大型接地系统的测量应用[5]。 袁培等人在平行布线的情况下采用多次移动电压极的方式对电阻和电感分量进行拟合以消去互感分量[9]。

在过往研究中仅考虑平行布线的互感， 并没有针对其他布线方式互感的研究， 往往导致接地阻抗测量结果偏大从而给接地工程带来不必要的降阻负担。 另外， 目前在评估引线互感时地下回流电流镜像穿透深度计算公式多取文献[12] 的近似结果，文献[12] 也指出了更为准确的穿透深度公式。与文献[12] 不同的是， 文献[8] 根据输电线路的暂态过电压模型选取2 倍趋肤深度作穿透深度。目前没有研究分析不同穿透深度公式的准确性， 给互感校正带来困难。

本文从接地测量的互阻抗基本理论入手， 提出了任意布置的接地测量引线互感分析方法， 并实现了互感的复镜像算法求解， 并与不同的穿透深度计算公式作对比。 在验证方法有效性的基础上分析了各种工况下互感数值的规律， 为校正接地阻抗受测量引线互感影响提供参考。

1 互感问题的理论分析

早在1946 年， Sunde 在文献[15] 中推导了任意两导体间互阻抗的通用公式。 存在任意布置的两直线引线L1和L2， 俯视图如图1 所示。 假设AB是L1的两个端点， CD 是L2的两个端点。 L1与L2间的夹角为θ。

图1 引线互阻抗的模型

假设大地电导率为σ、 介电常数为ε 和磁导率为μ， L1与L2间的互阻抗Zc计算公式为[15]:

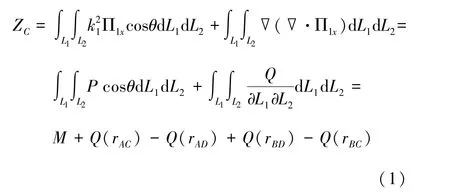
其中，

k1和k2分别为空气(介电常数为ε0和磁导率为μ0) 的波数和土壤的波数:

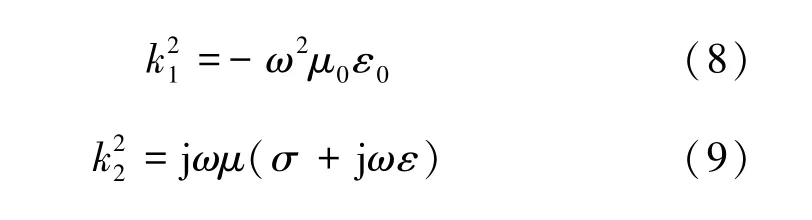
对比公式(3) 与公式(4)， Q 表示A、 B、 C、 D四点间的互电阻耦合， 与互感无关， 可以使用恒流场方法进行求解[12]。 接地测量引线互感M 为:

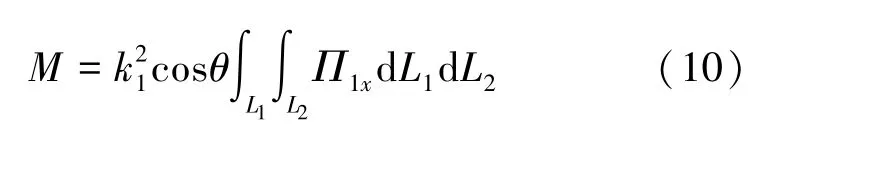
其中，

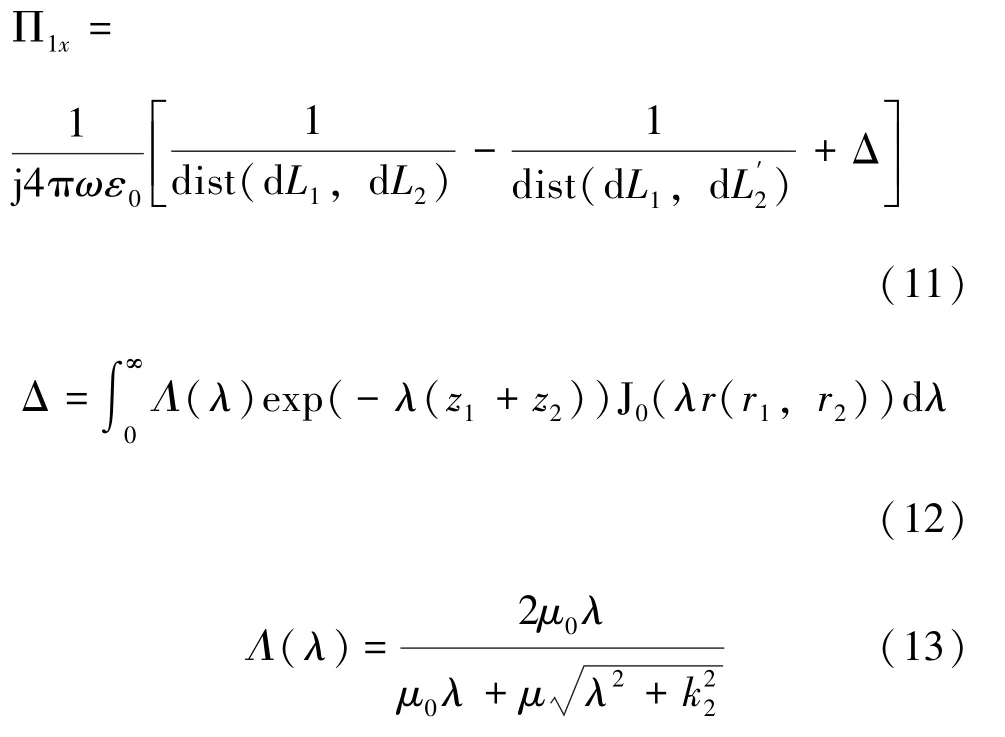
其中， dist 为距离函数， dist (dL1，dL2) 表示L1和L2上两微段dL1和dL2的距离； 同理，表示dL2关于地面的镜像。 在均匀土壤或者水平多层土壤的情况下， 互感修正项Δ计算公式可采用复镜像法来进行求解。 用复镜像来拟合式(13)， 有[16-17]:

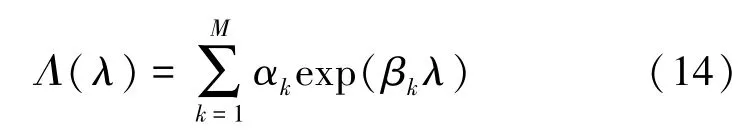
式(14) 代入式(12) 有:

把复镜像形式 (15) 代入互感计算公式(10) 有:

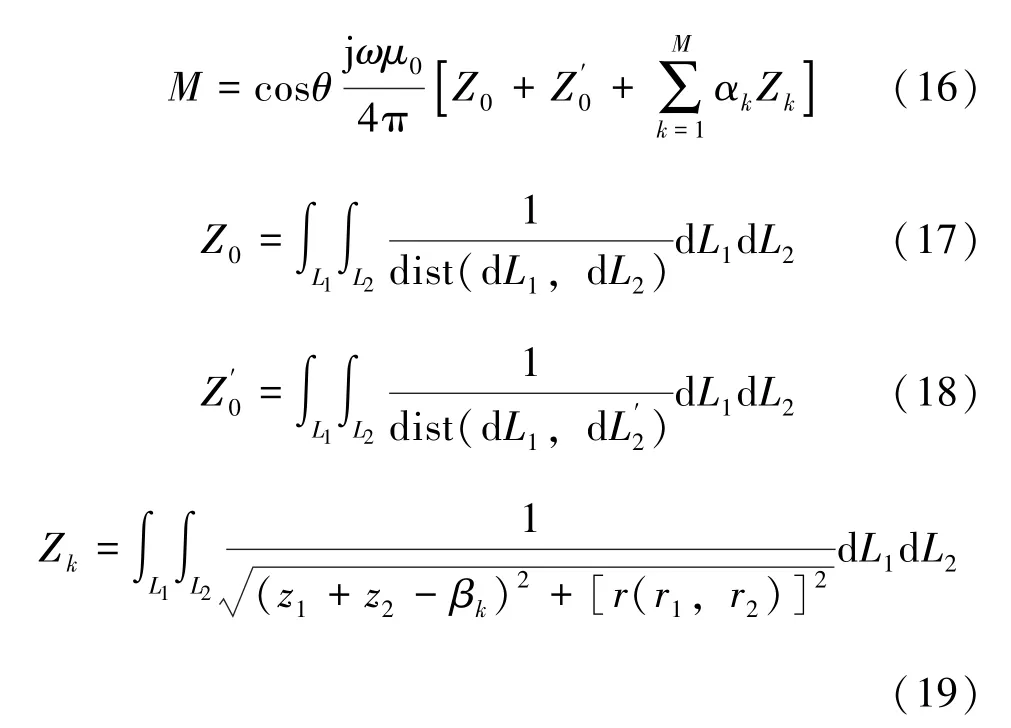
Z0和的理论表达式可由Heppe 公式导出[18]， 而Zk的理论表达式可以在复镜像位置和大小的基础上代入Heppe 公式以实现求解， 也可以对式(19) 直接进行数值积分求解， 在此不再展开。 下面列举算例， 取工频50 Hz， 大地电阻率为100 Ω·m， 接地测量电流引线长20 km， 采用5D-0.618 法， 电压引线与电流引线相距1 m， 引线布置于地表。 运用本文的复镜像法和数值积分法， 对比过往研究中不同版本的穿透深度。

目前应用最广泛的工频穿透深度De公式为[12]:

文献[12] 认为更严谨的穿透深度公式为:

文献[8] 选取2 倍趋肤深度作穿透深度为:

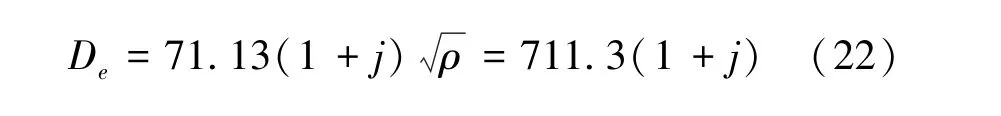
复镜像法和数值积分法的结果均为5.338 Ω，两者之间误差约为10-4Ω。 穿透深度取公式(20)时， 互感的计算结果为5.167 Ω， 穿透深度取公式(21) 时， 互感的计算结果为5.281 Ω， 穿透深度取公式(22) 时， 互感的计算结果为5.311 Ω。

公式(20) — (22) 均是对公式(13) 的单项指数形态拟合， 三个公式之间的结果有一定差别， 公式(22) 的精度最高， 公式(20) 精度最差。 尽管公式 (22) 在工频情况下的误差小于1%， 但本文的方法是更为精确的理论和数值方法，所得结果准确有效。 下面是不同工况下的互感计算分析。

2 互感计算分析

电流线L1和电压线L2的示意如图1 所示， 并约定C 点相对A 点的坐标为(X， Y)。 下面研究不同布线方式(5D-0.618 法、 2D-30 度夹角法、90 度夹角法、 反向法) 在不同引线长度和土壤电阻率情况下的互感。

2.1 5D-0.618 法

5D-0.618 法为引线同向平行布置的情况， 互感问题最为突出。 取大地电阻率100 Ω·m， 令X=0 m， Y=0 m、 5 m 和10 m 等三种情况进行分析，结果如图2 所示。

计算结果表明， 平行布线方法的互感与引线长度近似成正比， 而且受引线间距离的影响较大。 所以大型接地网应尽量避免采用5D-0.618 法测量接地阻抗， 即使是使用5D-0.618 法也需要尽量错开电压引线和电流引线的距离至5 m 或以上， 距离超过5 m 后影响不大。 取大地电阻率1 000 Ω·m， 互感计算结果如图3 所示。 结果与大地电阻率取100 Ω·m的情况类似， 只不过互感问题更为严重，这是由于地下回流镜像的穿透深度更大导致的。 若大地电阻率无穷大， 则相当于穿透深度无穷大， 这与不考虑大地影响的理论预期一致。

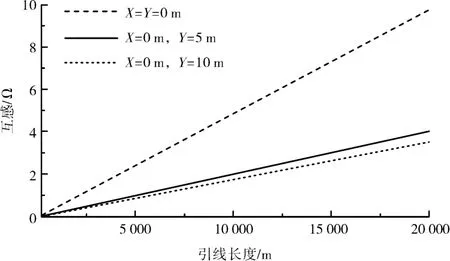
图2 互感与引线长度的关系(5D-0.618 法，大地电阻率取100 Ω·m)

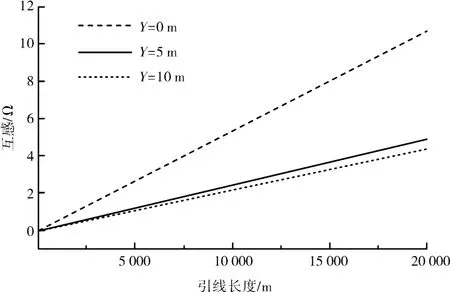
图3 互感与引线长度的关系(5D-0.618 法，大地电阻率取1 000 Ω·m)

2.2 2D-30 度夹角法

采用2D-30 度夹角法， 令测量引线长度L1=L2， 取大地电阻率100 Ω·m， 互感计算结果如图4所示。

图4 互感与引线长度的关系(2D-30 度夹角法， 大地电阻率取100 Ω·m)

由计算结果可知， 与5D-0.618 法布置情况下互感正比于引线长度的情况不同， 2D-30 度夹角法的互感随着引线长度的增加呈现饱和增长的趋势。 在测量引线长度大于20 km 的情况下可以认为互感增长进入饱和阶段。 图5 结果表明， 使用2D-30 度夹角法的情况下， 错开引线的距离可以减少互感， 但效果有限， 在测量引线长1 km 的情况下，互感约为0.06 Ω。 在测量引线长度取无穷大的情况下， 此时互感约为0.13 Ω。

图5 互感与引线长度的关系(2D-30 度夹角法， 不同大地电阻率)

取大地电阻率1 000 Ω·m。 在测量引线长1 km的情况下， 互感约为0.075 Ω。 在测量引线长度取无穷大的情况下， 此时互感约为0.4 Ω。 由于100 Ω·m 土壤电阻率对应的无穷长引线互感仅为0.13 Ω， 所以在大地电阻率较高的地方进行大型接地系统的接地阻抗测量时应尽量避免使用2D-30度夹角法。

2.3 90 度夹角法

采用90 度夹角法时互感恒为0， 所以在现场条件允许的情况下， 采用90 度夹角法可以完全消除互感的影响。 但需要说明的是， 由于90 度夹角法的电压极布置无法做到完全的电位补偿， 故测量数据需要除以一个修正系数来校正电压极位置不在补偿点而引入的测量误差， 即校正公式(1) 中Q的影响[6，10]。

2.4 反向法

采用 反 向 法， 取 大 地 电 阻 率100 Ω·m、1 000 Ω·m和10 000 Ω·m 等三种情况， X=Y=0 m， 计算结果如图6 所示。 可以看出， 使用反向布线的方式互感为负值， 大地电阻率100 Ω·m 时互感大小一般不会超过0.05 Ω。 由于互感较小，故反向布线法是一种受互感影响较小的测量方法。结果表明， 大地电阻率取1 000 Ω·m 时， 互感大小一般不会超过0.09 Ω， 即使是大地电阻率取10 000 Ω·m时， 互感大小一般不会超过0.25 Ω。高阻地区的大型接地网测量采用反向法时要考虑互感为负的影响。 另外， 反向法也存在电压极不在电位补偿点的问题， 测量结果也需要进行手动校正[6，10]。

图6 互感与引线长度的关系(反向法)

2.5 互感与引线夹角的关系

令L1= L2， 取大地电阻率为100 Ω·m， 改变引线夹角， 观察互感随引线夹角的变化， 计算结果如图7 所示。 从计算结果可以看出， 在0 ～180°范围内， 互感先随引线夹角的增加而迅速下降， 夹角＞60°后呈现缓慢减小的趋势。 如果分别以互感小于0.05 Ω 和互感小于0.01 Ω 作为控制条件， 取大地电阻率为100 Ω·m 能够满足要求的引线夹角范围计算结果见表1。

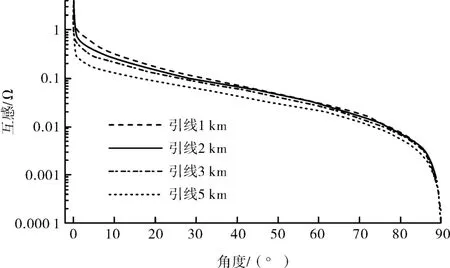
图7 互感与引线夹角的关系

表1 控制条件与引线长度对应的夹角范围

表1 结果表明， 如果是大型接地网需要使用夹角法测量接地阻抗， 建议测量引线夹角取为80°～105°。 夹角在90°附近对减少测量互感非常有利，但测量结果需要进行手动电位校正[6，10]， 需要事前进行分析以决定是否采用垂直布线的测量方式。

2.6 互感与大地电阻率的关系

令L1= L2， 取大地电阻率为1 ～10 000 Ω·m，改变引线夹角， 观察互感随大地电阻率的变化， 计算结果如图8 所示。 计算结果表明， 电阻率增加会使得互感增大， 而且互感增长的趋势呈现一定的饱和性。 鉴于5D-0.618 法和2D-30 度夹角法受大地电阻率影响较为明显， 建议加强测量布线范围的大地电阻率调研与测试， 以取得电阻率估算数据以准确评估互感大小。

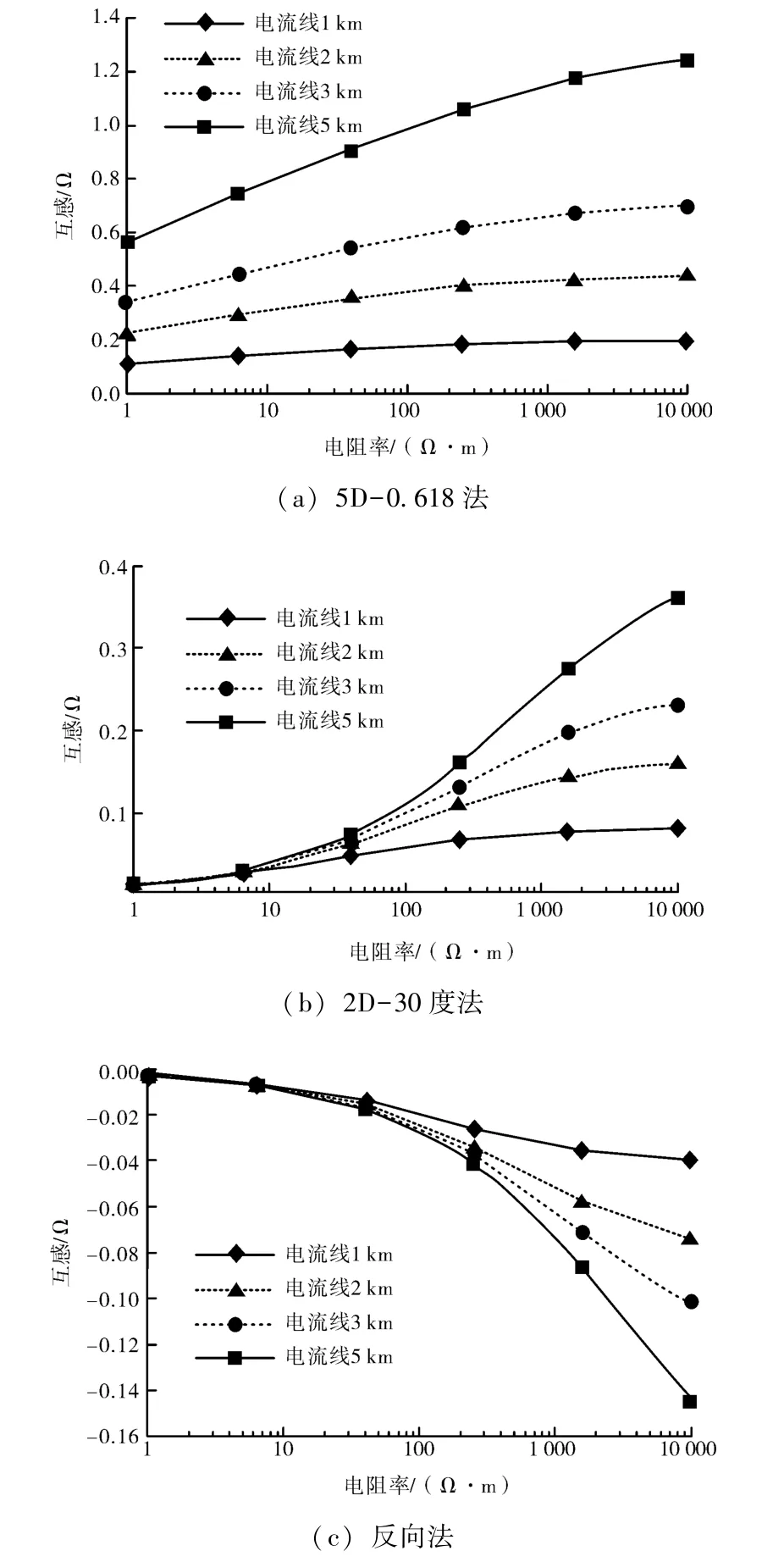
图8 互感与大地电阻率的关系

3 结论

本文基于电磁场理论和数值计算方法研究了接地阻抗测量中的引线互感问题， 结论如下:

1) 分析了完整的接地测量互阻抗理论模型，并提出了复镜像法的互感计算方案， 研究取得了不同布线方式(5D-0.618、 2D-30 度夹角、 90 度夹角、 反向)、 不同土壤电阻率情况下互感的数值分布规律， 分析了不同工况下互感对接地阻抗测量值的影响。

2) 在现场条件允许的情况下， 采用90 度夹角法可完全消除互感的影响。 5D-0.618 法的互感与引线长度成正比， 互感受引线间距离的影响比较大， 故大型接地网应尽量避免采用5D-0.618 法测量接地阻抗。 2D-30 度布线法的互感与引线长度存在饱和关系， 给出了不同土壤电阻率情况下的互感极限值供应用参考。 反向布线法的互感为负值，而且数值较小。

3) 电阻率增加会使得互感增大， 而且互感增长的趋势呈现饱和特性。 鉴于5D-0.618 法和2D-30 度夹角法受大地电阻率影响较为明显， 建议加强测量布线范围的大地电阻率调研与测试， 以取得电阻率估算数据以准确评估互感大小。