源于教材 发展于课堂
——核心素养与关键能力的落实
李振涛 王淑玲
(北京市顺义牛栏山第一中学)
课程标准是教学的依据,教材是落实课程标准的直接载体,教师是落实课程标准和教材的执行者和实践者,教师对课程标准和教材的理解直接影响到教学效果.充分利用教材,将教材中的例题和练习题进行深入的发掘和拓广,可以有效地减轻学生负担,达到提升学科素养和关键能力的目标,下面我们从教材的例题和习题出发,探索导数中放缩法的本源.
一、题目
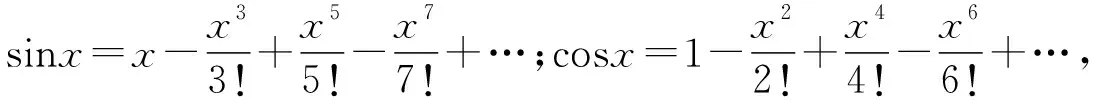
2.人教A版选择性必修第二册P97,练习1:利用函数的单调性,证明下列不等式,并通过函数图象直观验证:sinx 4.人教A版选择性必修第二册P94,练习2:证明不等式:x-1≥lnx,x∈(0,+∞). 5.人教A版选择性必修第二册P99,第12题:利用函数的单调性,证明下列不等式,并通过函数图象直观验证: (1)ex>1+x,x≠0; (2)lnx 1.题目1与题目2拓广探究 (1)当x>0时,sinx 【证明】sinx 所以可令f(x)=x-sinx,x>0,则f′(x)=1-cosx,易知在x∈(0,+∞)上f′(x)≥0, 所以f(x)在x∈(0,+∞)上单调递增,即f(x)>f(0)=0, 所以x-sinx>0在x∈(0,+∞)上恒成立,则sinx 由(1)可知m′(x)>0,所以k′(x)在x∈(0,+∞)上单调递增,所以k′(x)>k′(0)=0,同理可得f′(x)>f(0)=0,所以f(x)在x∈(0,+∞)上单调递增,所以f(x)>f(0)=0, 2.题目3,4,5的拓展探究 (1)指数ex≥x+1切线的放缩的推广. ①下面对其原式“加减乘除”并进行推广: 如果把原式x替换成x+a,则原式变成ex+a≥x+a+1,切点x=-a. 如果把原式x替换成x+lnx,则原式变成xex≥x+lnx+1(x>0),切点x+lnx=0⟹x0≈0.568. 如果把原式x替换成x-1,则原式变成ex-1≥x,又可表示为ex≥ex,切点x=1; ②下面对其原式“丢1换x”并进行推广. 如果把原式1丢掉,则变成: (2)对数lnx≤x-1(x>0)切线的放缩推广. 下面对其原式“加减乘除”并进行推广. 如果把原式x替换成1+x,则原式变成ln(1+x)≤x(x>-1). 从上面的代换可以发现,所谓导数中的“大招”其来源还是教材中的典型例题或习题的变形,这些所谓的“大招”只要教师在授课过程中稍加渗透就可以了. A.c>b>aB.b>a>c C.a>b>cD.a>c>b (Ⅰ)当a=0时,求f(x)的最大值; (Ⅱ)若f(x)恰有一个零点,求a的取值范围. 当x∈(0,1)时,f′(x)>0,f(x)单调递增; 当x∈(1,+∞)时,f′(x)<0,f(x)单调递减,所以f(x)max=f(1)=-1. ①当a≤0时,ax-1≤0,所以当x∈(0,1)时,f′(x)>0,f(x)单调递增; 当x∈(1,+∞)时,f′(x)<0,f(x)单调递减, 所以f(x)max=f(1)=a-1<0,此时函数无零点,不符合题意; 所以f(x)有唯一零点,符合题意; 这时候就要从题目要求出发,进行选择性调整,目标是解决f(x0)≥0,所以将-(a+1)lnx进行放缩,有两条途径:一是选择-(a+1)(x-1)≤-(a+1)lnx,我们试验一下看能否成功: 整理得到x2-(a+1)x+1≤0. 由二次函数g(x)=x2-(a+1)x+1的性质可知当0 命题得证; 令F(t)=-t2+2(a+1)t-a-2,则F(0)=-a-2<0, 所以f(x)恰有一个零点. 综上可知,a的取值范围是(0,+∞). 高考对高中教学起到重要的引导作用.高考评价体系将“引导教学”纳入核心功能,有利于理顺教考关系,增强“以考促学”的主动意识.从这个角度讲,高考不仅仅是对学生的选拔考试,也是对教师教学的一次评估,更是对教师在课堂中落实“立德树人、服务选材、引导教学”的一次评估,所以做好高三复习对于教师就是一次非常有挑战性的工作,也是非常具有创新性的工作,需要教师付出大量的时间和精力,不仅要在“一核四层四翼”上下功夫,还要着眼于学生的未来发展.现在的高三复习经常见到的现象是订阅一些教辅材料,通过教辅材料中大量的习题巩固基础知识与基本方法,教材经常被束之高阁,偶尔使用一下.教材是落实“一核四层四翼”的基本载体,如何用好教材进行复习是一个值得研究的问题.上面例子说明教材中的试题与高考试题之间有非常高的相关性,通过对教材中例题和练习题的多角度拓广使其能够对接到高考试题中,就能够实现减负增效,提升学生核心素养和关键能力的目标.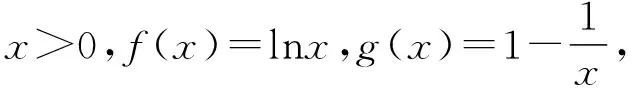
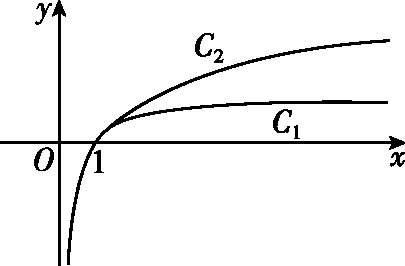
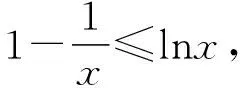
二、构建知识网络
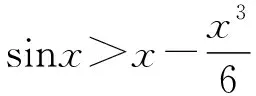
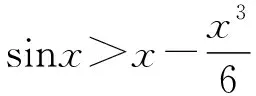
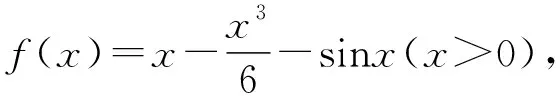
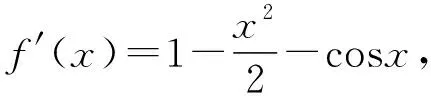
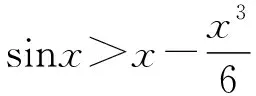
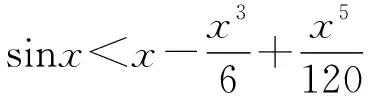
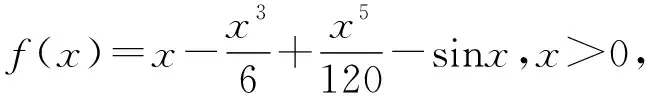
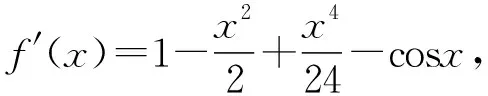
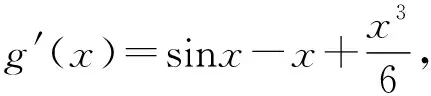
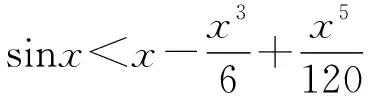
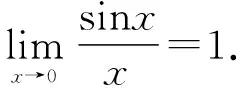
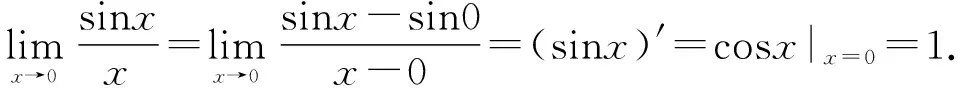
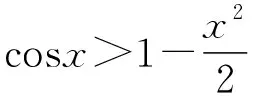
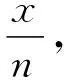


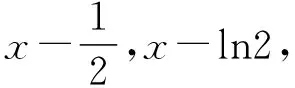
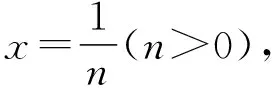
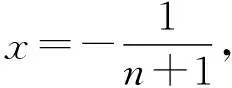
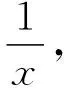
三、典型应用
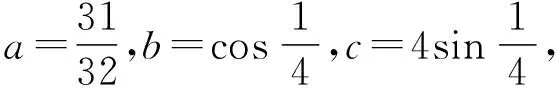
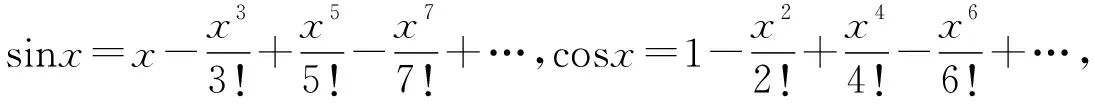
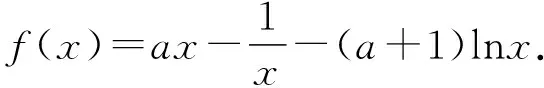
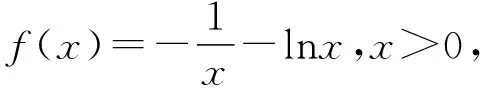
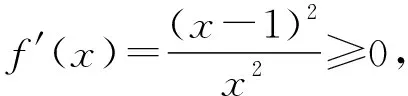
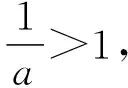
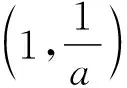
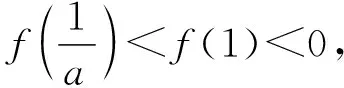
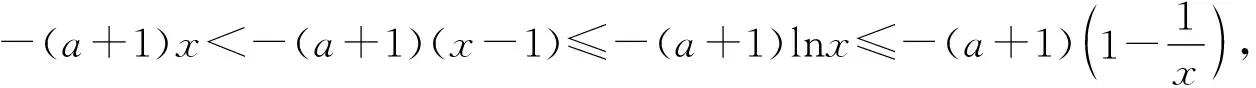
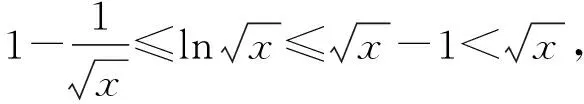
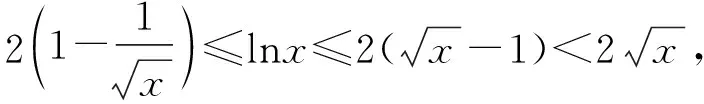
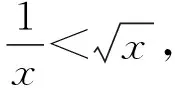
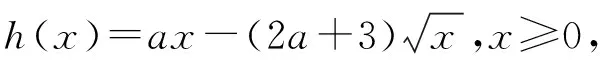
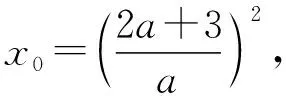
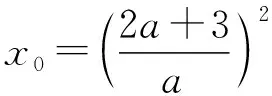
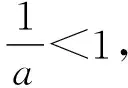
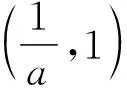
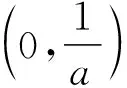
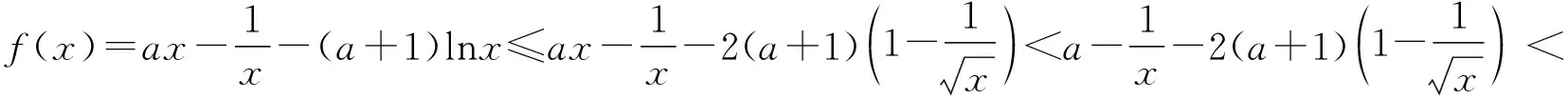
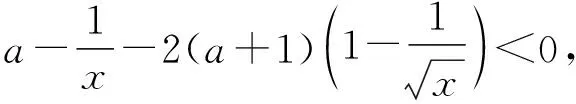
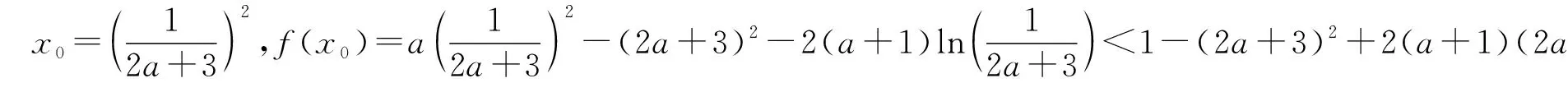
四、教学建议

