亚波长铌酸锂薄膜导模共振结构设计及二次谐波转化效率优化
曹春雨 ,瞿敏妮 ,谢 微
(1.华东师范大学 精密光谱科学与技术国家重点实验室,上海 200241;2.上海交通大学 电子信息与电气工程学院 先进电子材料与器件平台,上海 200240)
0 引言
铌酸锂(LiNbO3,LN) 因其优异的光学性能而被认为是光学领域的关键材料[1-5],被誉为“光学硅”.近年来,在低折射率衬底上成功地制备出亚微米厚度的铌酸锂单晶薄膜,开启了绝缘体–铌酸锂结构(lithium niobate on insulator,LNOI) 的新性能应用[6-8].依托于LNOI 高折射率对比度,人们制备出了低损耗波导[9-10]、微盘微环谐振腔[11-14]、超高速电光调制器[15-18]、周期性极化铌酸锂非线性器件[19]、宽带光学梳[20-21]和光子晶体[22-24]等高性能的微纳光电器件.LN 由于其非中心对称结构而具有较大的二阶非线性系数(χ(2)),结合其在超宽光谱范围内具有极低吸收率的性质,它是可见光–紫外波段二次谐波产生(second harmonic generation,SHG) 的完美材料.为了提高二次谐波转化效率,人们采用准相位匹配的方法用于补偿相位失配[25],又开发出梯度超表面用于提高二次谐波转换的效率[26].然而,当非线性介质薄膜厚度在亚波长尺度时,基频光透射薄膜样品产生的二次谐波转化效率往往极低.为了增强亚波长尺度LNOI 的非线性响应,利用高品质因子(Q值) 光学微腔增强光场的局域功率密度是一种可取的方案.
人工微纳结构可以在亚波长尺度实现对光子的捕获,从而获得高密度的局域电磁场能量,这是在极小的模式空间内操控光场的重要手段之一,在增强光学非线性方面有着重要应用[27-29].近年来,介质光学超表面在提高光与物质非线性相互作用方面取得了进展,在理论和实验上,高Q值的谐振腔结构都实现了二次谐波的高效转化[30-31].导模共振(guided mode resonance,GMR) 微纳结构是一种由光栅和波导结构衍生出的复合结构,其包含超表面光栅结构,以及由高折射率、低折射率介质层组成的波导层.当波导层厚度处于亚波长尺度时,极小的模式体积和较高的Q值参数可使GMR 微纳结构在加强光与物质相互作用方面有优良的表现,常被应用于光学滤波、光学非线性和生物传感器等领域[32].在理想的导模共振结构体系中,连续谱的束缚态(bound states in the continuum,BIC),即所谓的“暗态”[33],被证明具有完美的光场限制能力,拥有无穷大的Q值[34].光学BIC 首先在光子平板晶体中被发现[35].然而理想的BIC 无法被外场所激发,因此无法被直接利用.但是近来的研究表明,对于BIC 结构,通过打破其结构对称性或破坏动量空间的对称性,可以使理想的BIC 模式衰退成准BIC 模式[36-37].准BIC 模式仍具有大的Q值,但却可以被外场所激发.利用准BIC 模式的超高Q值并结合LN 所具有的大的二阶非线性系数,本文提出了在亚波长厚度LNOI 样品表面刻蚀GMR 超表面结构,并通过理论模拟证明了紫外波段二次谐波的显著增强效应,其增强比例高达105数量级.
本文后续: 第1 章介绍刻蚀GMR 的LNOI 模型结构;第2 章模拟GMR 超表面结构的各参数对于透射光谱的影响,重点分析对共振波长以及半高宽等参数的影响,探究不同偏振态以及不同入射角度对透射光谱的影响,利用非对称结构制备高Q值的准BIC 模式,并利用局域场增强实现LNOI 样品的SHG 效率提升;第3 章对全文做出总结.
1 模型简介
本文研究的全介质光栅结构如图1(a)所示: 基于“三明治”结构的铌酸锂(LN)薄膜平台,自上而下分别为亚微米厚度的LN 薄膜、二氧化硅(SiO2) 隔离层以及LN 衬底层,其中LN 薄膜和SiO2的厚度分别为h1和h2.这样,高折射率的LN(其折射率约为2.2) 和SiO2(其折射率约为1.45) 便形成了大的折射率对比度,为限制光场提供了有力支持.通过在LN 薄膜层刻蚀凹槽以形成周期性的光栅结构.光栅的参数: 周期长度(D); 刻蚀深度(h) ;光栅条宽度(d) ;填充因子(F),其定义为光栅条宽度和光栅周期的比值,即F=d/D; 入射光的波矢为k,入射方向在yOz平面,其与法线夹角为θ;光源的偏振态定义为TM(transverse magnetic) 极化波电场,方向在yOz平面(即与光栅刻线垂直),TE(transverse electric) 极化波电场沿着x轴方向(即与光栅刻线平行).为了激发出导模共振效应,光栅结构的相位匹配需要满足方程[38]
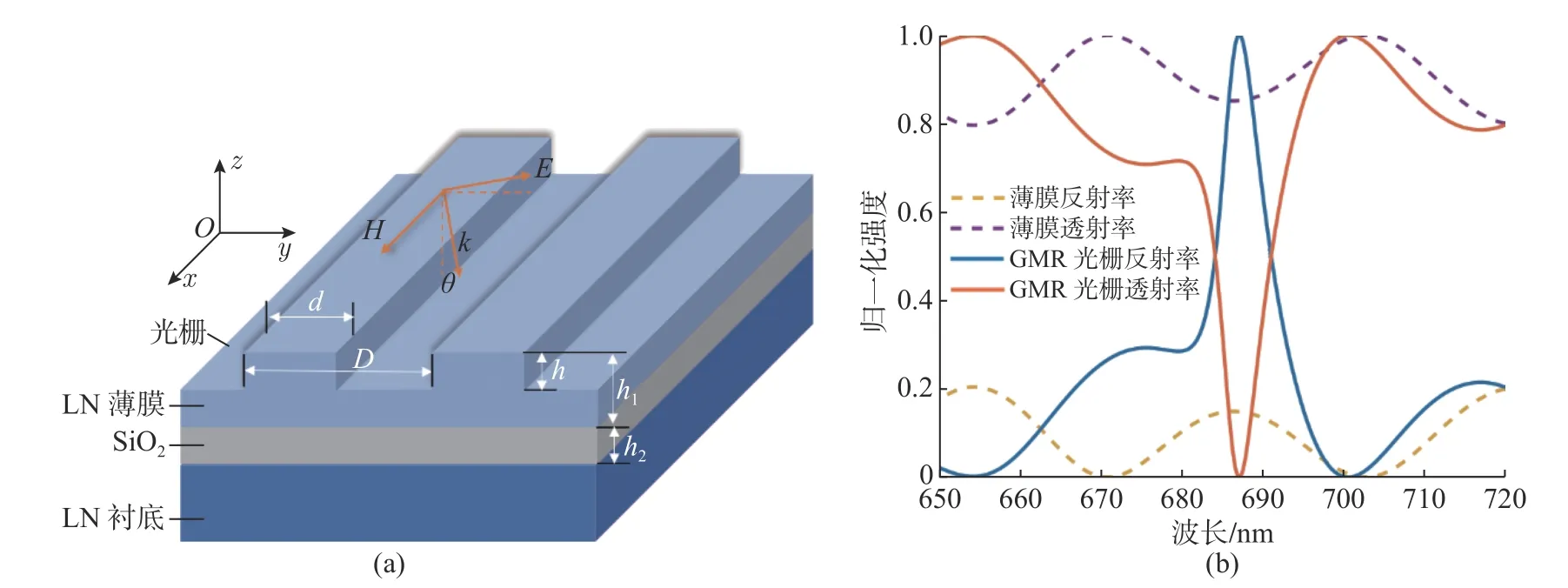
图1 (a) GMR 光栅结构示意图;(b)未刻蚀结构的铌酸锂薄膜与添加GMR 结构的铌酸锂薄膜的光谱信号对比Fig.1 (a) Schematic of the GMR grating structure;and(b) spectrum contrast of unetched lithium niobate film and GMR grating structures
式(1) 中:nc为覆盖层的折射率(在本文的结构中,覆盖层为空气);nS为SiO2的折射率;λ为入射波的波长;neff为光栅的有效折射率;i为光栅的衍射级.
根据式(1) 可以通过调整光栅参量初步确定共振波长.本文主要关注的波段为可见光波段,对其光栅结构的光学性质求解,仿真采用时域有限差分法(finite difference time domainmethod,FDTD).由于本文的结构是周期性重复结构,故只需要对单元结构仿真便可以求解整个空间内的电磁场分布.在x方向和y方向设置周期性边界条件,在光场的传播方向,即z方向使用完美匹配层边界条件(perfect matched layer,PML).由于LN 属于负单轴晶体,因此数值模拟不仅需要考虑LN 的色散性质,同时还要关注其双折射的影响.这里异常光折射率(ne) 和寻常光折射率(no) 均采用Zelmon 等[39]的文献数据.
基于h1=300 nm、h2=4µm 的z切向LN 结构,采用可见光波段的宽光谱平面波光源正入射到结构表面,入射光偏振态为TM 偏振.图1(b)给出了未刻蚀的LN 薄膜的光谱以及GMR 光栅结构的光谱的对比: 黄色和紫色虚线分别是薄膜的反射谱和透射谱;蓝色实线和红色实线分别为GMR 光栅结构的反射光谱和透射光谱.光栅的结构参数分别为D=356 nm,F=0.7,h=70 nm.从图1(b)可以看到,在没有加光栅前,薄膜对入射光几乎是透明的,所有波长的入射光都可以高透通过,只有很小的一部分反射回来;但是在添加光栅结构后,光谱发生了巨大的变化,在特定的波长处反射率急剧地增加甚至接近1,此时的透射率相应地衰减接近0,在远离共振波长时反射率将会迅速地下降.这说明导模共振光栅结构改变了原有的近场分布,将共振处的光场局域增强了反射、减弱了透射,并且共振峰线宽仅约7 nm.导模共振,实际就是光栅的高级次子波和波导光栅的传播常数相当时所引起共振的现象.同时为了控制衍射效率,选择亚波长光栅结构(D<λ),保证透射波和反射波只有一个级次的传播,从而达到能量集中的效果.
2 结果与分析
2.1 光栅结构参数对于透射光谱特性的影响
为了探究光栅结构中各参数对于光谱信号共振峰的影响,本文采用控制变量法分别研究了宽光谱平面波光源垂直入射下,光栅周期(D)、填充因子(F) 和刻蚀深度(h) 对光谱的影响,仿真得到的透射光谱如图2(a)、图2(b)、图2(c)所示.为了直观地观察光栅周期对共振波长的影响,图2(d)给出了共振波长随光栅周期的变化.由图2(d)可以看到,共振峰的波长分依赖光栅周期(D) 的大小,当D从330 nm 变化到370 nm 时,共振峰从近650 nm 的位置移动到了705 nm 左右.从图2(a)(F=0.7,h=70 nm)可以看到,共振波长随周期变化的趋势近似为一条直线,相应的斜率约为1.45.由图2(b)(D=356 nm,h=70 nm)可以看到,填充因子(F) 对共振峰的波长位置影响较小,在F从0.5 到0.9 大范围变化的过程中,峰位仅发生红移约10 nm;但是当F较小时,共振峰一侧旁带的影响就越突出.从图2(c)(D=356 nm,F=0.7)可以看出,刻蚀深度(h) 对光谱的作用十分显著,当h较大(h>100 nm)时,共振峰的线型越宽;随着h的减小,其半高宽(full width at half maximum,FWHM) 也就逐渐减小,同时其共振峰一侧的旁带影响也变小.为了直观且定量地表述刻蚀深度对光谱的影响,图2(e)分别给出了h=150 nm,120 nm,90 nm,60 nm,30 nm 时透射光谱图,显然随着h的减小,共振峰的线宽越窄,但是峰谷的高度还是很低,接近0.图2(f)定量给出了FWHM 随刻蚀深度的数值变化,显然FWHM 随着h的减小而减小,当h=30 nm 时,FWHM 仅有1.9 nm.

图2 光栅各参数对透射谱的影响Fig.2 Influence of grating parameters on the transmission spectrum
从上面的分析可以看出,周期直接决定了共振峰的波长,使用不同的周期参数便可以设计需求的共振波长,并且在光栅的刻蚀深度很浅即只有几十纳米时,便可以获得线宽非常窄的共振峰.这说明LN 薄膜在引入较浅的光栅槽调制、对原有薄膜破坏较小时就可以十分显著地导模共振效应.由于LN 材料以及SiO2在宽谱范围内具有透明性,因此LN 导模共振光栅结构不仅可以反射式滤波,而且可以对透射光滤波.
2.2 光源的偏振以及入射角度对透射光谱的影响
本文的结构属于一维周期性光栅,其结构具有明显的方向选择性,因此对于不同的偏振态的入射波可能会有不同的光学响应.为此,本文重点研究了TM 和TE 这两种偏振态下,不同角度的平面波照射对结构的透射光谱的影响.图3(a)为TM 偏振光入射下的透射光谱.在正入射时,如图3(a)所示,只有1 个共振峰.但是当斜入射时,任意入射角度(θ) 下都会出现2 个共振峰,并且随着θ的增大,上方1 个峰会发生红移,同时下方1 个峰会蓝移,导致2 个峰彼此间的距离越来越远,这正对应着式(1)中i=1 和i=–1 这2 个衍射级的贡献,共振峰出现左右高度对称的情形,即T(λ,θ)=T(λ,-θ) .当保持光栅结构各参数不变(D=356 nm,F=0.7,h=70 nm),仅改变光源的偏振态,即由TM 偏振变成TE 偏振时,仿真的结果如图3(b)所示.由图3(b)可以看到,共振峰的位置整体都发生了红移,在正入射时,共振波长由约685 nm 变为约730 nm,出现了近似双曲线的共振分布,如同TM 偏振态也是关于中轴线左右对称.但是不同的是,上下两条能带发生了分离,出现了约10 nm 的光学带隙;同时可以看到,上面的能带谱线出现了奇特的现象,在接近0°时谱线线宽逐渐减小直至完全消失,即此时出现了导模共振的“暗态”模式.“暗态”模式由于对称性保护,无法被垂直入射的平面波所激发,在光谱图上即表现为线宽消失.这种“暗态”模式称作BIC 模式,处于连续谱中,但是能量被完全束缚住,无法激发,理论上Q值为无穷大.
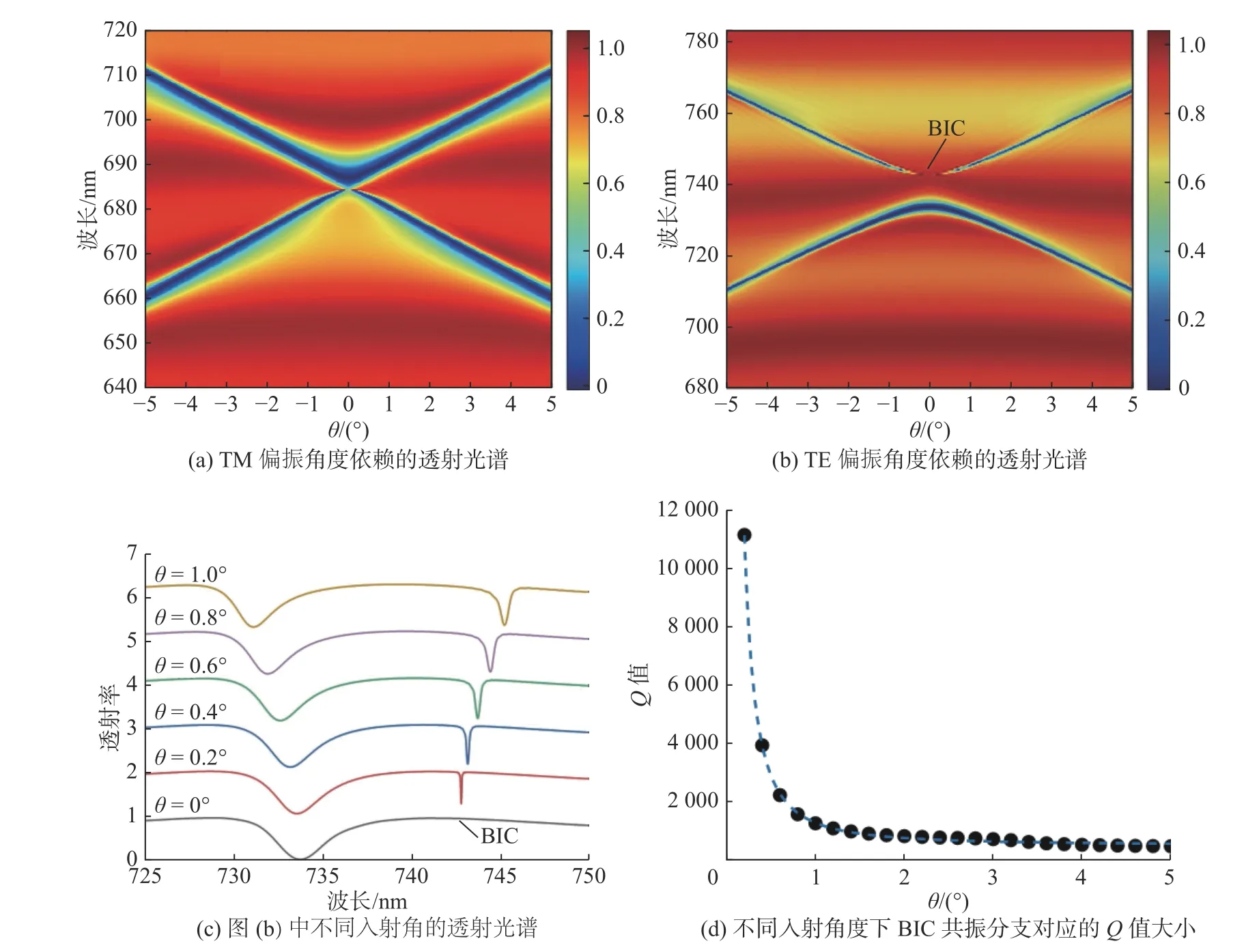
图3 光源偏振和入射角度对光谱的作用Fig.3 Role of polarization and incidence angle of the light source on spectra
为了进一步探究BIC 模式,本文将图3(b)中θ=0°,0.2°,0.4°,0.6°,0.8°,1.0°的透射光谱提取出来绘制在图3(c)中.当θ从1°逐渐减小时,透射谱右侧的共振峰波长向着短波移动,同时谱线的线宽也越来越小,直到θ=0°时,完全看不到峰的BIC 模式.图3(d)给出了θ在0°到5°范围内Q值的变化,Q值的定义是Q=λ/δλ,其中λ为共振峰的波长,δλ为共振峰的半高宽.在θ=5°时,Q值只有约300;随着θ的减小,Q值呈现指数级增长的趋势,当θ=0.2°时,Q值达到约1.1 × 104,这说明入射角度越小,其对光场的限制能力就越强,从而把能量集中在光栅所在的LN 薄膜层,加强了光与物质的相互作用,故具有非常大的Q值;当θ=0°时,由于其无法被外界的任意偏振态的光源所激发,即使在理论上存在无限大的Q值,也无法直接利用,反而破坏对称性的斜入射时,理想BIC 模式转变成准BIC 模式,仍然保持非常大的Q值,常常能够被实际利用.
2.3 非对称结构的共振增强与二次谐波增强
BIC 模式除了在动量空间能够实现,其结构对称性被破坏时也能够出现准BIC 模式.为此,本文仍然基于前面的结构,不同的是,光栅不再是单周期地无限重复,而是存在双周期的单元(图4(a)),其大的周期(D)=2da+db+dc,光栅条的长度为da=0.25D.这样结构就不再对称,而是沿着da+db和da+dc交替周期性地排列.为了表征结构的非对称程度,定义非对称系数δ=(db-dc)/(db+dc),显然δ取值范围为 [0,1] : 当δ=0 时,结构是对称的;当δ=1 时,表示dc为0,即右侧的空气槽完全消失.考虑到LN 的各向异性,为了后面更好地获得LN 的二次谐波响应,本文采用x切向的LN,但是LN 薄膜的厚度和SiO2的厚度保持不变(h1=300 nm,h2=4µm).

图4 非对称GMR 结构设计及线性光学性质Fig.4 Asymmetric GMR structural design and linear optical properties
在研究非线性之前,先需研究其线性光学性质,理解其作用机理.为此本文仿真采用图4(a)所示的结构,其中D为374 nm,h为70 nm,模拟不同δ值时,在TE 偏振光入射下其透射谱线的性质.与前面动量空间的BIC 类似,研究的结构在其结构对称性没有被破坏(δ=0) 时出现理想的BIC 模式,即线宽消失;当结构的对称性被破坏时,理想的BIC 模式就会变成可探测的高Q值的准BIC 模式.图4(b)给出了δ=0.1,0.2,0.3,0.4,0.5 时的结构透射光的谱线: 当δ值减小时,共振峰的波长向短波方向移动,且此时线宽逐渐变小,直到δ=0 时共振峰完全消失.图4(c)给出了δ=0.1,0.5 时其电场对于入射光的归一化分布:δ=0.5 时,场增强的最大处数值为16 倍;但是δ=0.1 时,场增强的最大数值为80 倍,此时电场主要分布在刻蚀光栅的LN 层,这也进一步说明了结构的δ越小对于光场的局域效果越好.
为了定量描述场局域效果,图4(d)给出了其Q值随着δ变化的情况: 当δ=0.1 时,Q值高达1.45×104;当δ增大时,Q值迅速衰减,在δ=1 处Q值仅约145;对Q值和 1/δ2进行线性拟合,说明Q值正比于 1/δ2,在δ较小时,由于形成准BIC 模式,在光栅结构非常小的模式体积中形成了强烈的局域场增强,品质因子也达到了很高的水平.
以往的研究表明,强的光场局域对于提高微纳结构的非线性响应至关重要.在本文的研究中,重点关注的是其Q值最大(δ=0.1) 处的非线性效应.由于LN 属于3m 点群晶体结构,其非线性张量(dijk)可以表示为
LN 是负单轴的双折射晶体,其二阶非线性系数为d33=27 pm/V,d31=4.6 pm/V,d22=3 pm/V .因此在足够强的基波(fundamental wave,FW)的泵浦下,LN 内部形成的二次谐波极化强度为
为了获得更强的二次谐波响应,本文利用最大的非线性系数d33.对于SHG 的仿真,选择非耗尽的泵浦近似.由前面关于非对称结构的线性光学性质的讨论可以发现超高Q值出现在约731 nm,同时为了利用d33,选择TE 偏振态(偏振方向沿着x切向LN 的光学轴,即图4(a)的z轴方向) 的强场光源垂直入射泵浦.为了评价其SHG 的响应效果,本文在结构的透射方向对相应面积内的坡印廷矢量做积分,以得到SHG 的转化的功率值.二次谐波的转化效率(η) 定义为二次谐波的峰值功率与基波(FW)的峰值功率之比,即
考虑到实际的应用,SHG 和FW 的光强依赖关系也被研究.FW 的峰值光强由0.12 GW/cm2到1.33 GW/cm2逐渐变化,SHG 的光强随着FW 光强的变化如图5(a)所示.表明SHG 的功率密度和FW 的泵浦激发功率密度的双 l og10坐标,拟合斜率约为2 的线性关系,即二次谐波的光强正比于入射基波光强的平方(对应电场强度的四次方).

图5 二次谐波的增强Fig.5 Enhancement of second harmonics
图5(b)给出了本文这种结构在δ=0.1 时,SHG 的转化效率随FW 泵浦强度的变化: 当FW 峰值光强为1.33 GW/cm2(对应电场振幅值为1 × 108V/m)时,其二次谐波的转化效率为0.58%;当光强为0.133 GW/cm2时,其转化效率为0.06%.SHG 的效率随FW 的光强呈线性变化,也进一步证明了二次谐波的产生.
SHG 在不同波长泵浦下的转化效率如图5(c)所示,在共振处(FW 波长约731.2 nm,SHG 波长约365.6 nm) 其SHG 的转化效率最大,η为0.58%.在LN 薄膜仅数百纳米厚度的情况下,二次谐波依赖相位匹配的传播距离十分有限,未刻蚀光栅的LN 薄膜其SHG 转化效率只有约10–8,但是通过刻蚀光栅结构,在局域场增强的作用下,可以使得结构的SHG 的转化效率增强约 1 05倍.同时可以看到,在稍微偏离共振波长的位置,其SHG 的转化效率呈指数级下降,这是因为共振处Q值高共振线宽十分窄,一旦远离共振处其光场的局域效果将会迅速下降,对于二次谐波的增强效果也将不再明显.
3 结论
本文在理论上设计了基于LN 薄膜的亚波长导模共振光栅结构,数值分析了结构参数以及光源偏振态和入射角度对于其共振特性的影响.结果表明,光栅周期决定了共振波长的位置,并且刻蚀深度对共振的线宽影响明显,刻蚀深度越小其线宽也就越小.同时研究了入射角度对于共振峰的线宽的影响,设计了非对称的光栅结构,实现了Q值为 1.45×104的准BIC 共振模式,利用超高Q值的局部场增强实现了对于LN 的二次谐波的共振增强.当非对称系数δ=0.1 时,在泵浦光峰值功率为1.33 GW/cm2下,实现了0.58%的SHG 转化效率.

