退相干演化对Jaynes-Cummings 模型影响的考察

黄艺漫,马 雷

（华东师范大学 物理与电子科学学院,上海 200241）

0 引言

量子理论是20 世纪科学发展进程中最重要的物理理论之一,其对推动现代科学技术进步的作用不言而喻.利用量子理论来研究并设计量子器件,是目前量子信息领域重要的研究方向.在量子力学中,量子计算、量子态制备等在很大程度上依赖量子系统的相干性.量子力学中的相干性是其区别于经典力学的一个根本特性,而量子计算机的运作依赖维持量子态的相干演化,需要抑制环境的干扰.所以实现精密量子测量的一个关键问题便是控制原子与腔场相互作用体系中的退相干效应.

在量子力学中,开放量子系统的量子相干性会因为体系与外在环境发生大量的量子纠缠,随着时间的演化过程逐渐丧失,这个效应称为量子退相干,是量子系统与环境由于量子纠缠而产生的结果.由于退相干的发生,量子相干性产生的干涉现象会消失无踪.量子退相干促使系统的量子相干行为变迁成经典行为,这个过程称为“量子至经典变迁”.该问题最早是由H.Dieter Zeh 在20 世纪60 年代提出,进而催生出了退相干理论(也称作动力学退相干或者环境诱导退相干);20 世纪80 年代,退相干的研究得到了进一步发展,H.Dieter Zeh 等提出了第一个具体的退相干模型[1].1991 年,Zurek[2]在Reviews of Modern Physics(《现代物理评论》)中更广泛地提出了退相干理论中的重要因素.到今天,在量子力学需要实现现实应用与推进的背景下,退相干越发成为量子力学中重要而迫切的理论分析问题.自20 世纪80 年代初首次对方案进行精确的公式化以来[3-6],到2000 年孙昌璞等[7]成功解释了量子态跳变现象,并给出了系统退相干的根本特征—在时间趋于无穷大时,密度矩阵的非对角元项会衰减至0,退相干问题对量子力学基础理论的影响越发成为量子信息技术领域重点关注的问题.

Jaynes-Cummings 模型[8-9](简称J-C 模型) 是描述原子与光场相互作用的理想模型,最初由Jaynes 和Cummings 于1963 年提出,Rempe、Walther 和Klein 于1984 年首次进行了实验证明[10].在量子光学中,J-C 模型是一个基本的理论模型,主要用来描述一个两能级原子与单模量子光场之间的相互作用.近年来,由于其可以精确求解、易于扩展的特点,人们对它的各种物理属性进行了深入、广泛的研究.

本文基于J-C 模型,对开放系统退相干时间演化后的量子态特性影响进行了考察与分析: 设定初态,采用Kraus 求和方法推导出了退极化模式下量子态发生退相干后的约化密度矩阵;在此基础上,分析了量子态退相干时间演化后的保真度、von Neumann 熵的变化情况.

1 J-C 模型与退相干模式

1.1 J-C 模型

1963 年,Jaynes 和Cummings 在讨论微波激射器时提出了标准的J-C 模型[8],该模型是量子光学中一个基础可解的理论模型.下面系统地给出该模型的哈密顿量(H).

光场与原子相互作用的总哈密顿量(H) 可以表示为

式(1)中:H0表示原子哈密顿量;HF表示单模自由光场哈密顿量;HI表示原子与光场相互作用哈密顿量.将能量零点选取在两能级之间,J-C 模型的系统总哈密顿量(H) 就可以表示为

式(2)中:ω0为原子的跃迁频率;ω为光子的频率;Sz是原子的自旋算符;S+、S-分别是原子向上、向下能级跃迁的跃迁算符;g为光子与原子的耦合常数,这里可设为实常数(如果是复常数,可以利用转动变换将复数幅角变换至产生、湮灭算符中);a+、a分别为光子的产生、湮灭算符; ℏ 为约化普朗克常数.于是在共振条件,即ω=ω0时,总哈密顿量(H) 用矩阵可以表示为(在|1,n+1〉态和|2,n〉态组成的子空间内)

J-C 模型下的初态由于光子数的差异可以写成很多种,也可以写出原子态与光子的直积态,例如,|1,n+1〉表示此时系统的量子态中原子处于下能级|1〉.光场光子数为n+1 ,量子态|2,n〉与此同理.

1.2 退相干模式

量子力学中的相干性是区别于经典力学的一个根本特性,量子信息的传播、处理、演化过程需要依赖量子态的相干演化,所以需要抑制环境、噪声等带来的干扰.从量子理论来看,封闭的量子系统时刻遵循幺正演化,但是在实际操作中量子系统却是普遍开放的,不存在完全孤立于外界与环境的封闭系统.外界与系统时时刻刻发生着信息纠缠、互换,所以量子态的实际演化一定伴随环境的影响,在这些影响下,量子态会逐渐失去相干性等特征,最后量子信息散失在环境中,发生量子退相干.

在对退相干问题的起源分析中,可能会来自如下的情况: ①子系统与环境(噪声) 耦合作用造成退相干;② 子系统在观测中的塌缩、跃迁造成退相干;③子系统的自发辐射、衰减、跃迁造成退相干.本文选取J-C 模型下一子空间的2 个基矢|1,n+1〉和|2,n〉,类比单qubit 信道演化过程[11]的衰减,对于原子与光子直积态,主要考虑退极化模式下的退相干效应.

退极化方式中,基并不稳定,会发生以下3 种误差翻转.

1)σx误差—位翻转误差

假设初态为|ψ〉,由有|ψ〉→σx|ψ〉,即假设体系子系统处于|1,n+1〉和|2,n〉这2个基矢.该种误差会使原子在|1〉,|2〉之间跳跃.

2)σz误差—相位翻转误差

假设初态为|ψ〉,由,有|ψ〉→σz|ψ〉,即假设体系子 系统处于|1,n+1〉和|2,n〉这2 个基矢.该种误差可能会使量子态发生相位翻转.

3)σy误差—混合型翻转误差

假设初态为|ψ〉,由,有|ψ〉→σy|ψ〉,即子系统会发生上述2 种误差的混合误差翻转的情况.

本文用一个幺正算符

来表示误差的发生.式(4)中:n=x,y,z,表明子系统的初态分别发生了σx,σy,σz这3 种误差翻转;|i〉E,i=0,1,表示环境态.

同样地,也可以假设这3 种误差同时等概率发生,表示为

后文将给出拟合图进行对比,分析哪种误差对系统的量子态性质影响最大.

2 退相干效应对体系保真度的影响

基于J-C 模型,设定光场与原子相互作用子系统的初态

其中,|i,n〉表示原子处在i能级(i=1,2) 而光场有n个光子的状态.由于旋转波近似,相互作用哈密顿量只能导致|1,n+1〉与|2,n〉态之间的跃迁.

式(7) 中:Mn是一组作用在子系统 S 上的算符,它表示在系统 S 与环境 E 相互作用下对系统状态的影响;S可以认为是将子系统的初态映射到时刻,这种映射称为超算符映射,式(7)也称作超算符的求和表示,且由于退相干发生的时间十分短暂,可以认为是在瞬间发生,所以这里的时间可写作

本文讨论的是发生一次退相干后,系统随时间演化过程中量子态的变化.所以在得出退相干的约化密度矩阵之后,可以定义一个时间演化算符,来描述原子与光子子系统退相干后约化密度矩阵的动力学演化.时间演化算符为

其中的H为哈密顿量,且取式(2) 中原子与光子相互作用系统的总哈密顿量.由此,末态的约化密度矩阵便可以写为

Jozsa[12]根据“跃迁几率”首先提出了保真度的概念,定义了量子混态的保真度,并且从数学上证明出了保真度的一些基本性质.保真度(F) 的表达式为

式(10)中:ρ0为初态的约化密度矩阵算符;ρ为末态的约化密度矩阵算符.F∈[0,1] ,当F取左/右端点值时,可以分别认为是正交演化过程信息完全失真,以及末态与初态保持一致的理想演化过程.

在退极化模式下,本文分别考察了σx误差、σz误差、σy误差以概率P翻转,以及3 种误差等概率翻转的4 种情形.

设定一个初态

根据1.2 节,在退极化模式的σx误差、σz误差、σy误差以P概率翻转,以及3 种误差以概率混合翻转下,由式(7)得出每种误差翻转后子系统 A 的约化密度矩阵,分别为

将式(12)—(15)代入式(9)和式(10),可以计算出各反转误差后的保真度.取P=0.2,各误差的保真度对比详见图1.

图1 是非退相干演化与退相干演化后的保真度随时间演化的拟合图.图1(a)是无退相干的纯态演化,此时由于时间演化算符中含有时间因数,末态的保真度会随着时间演化发生有规律的振荡,这与理想J-C 模型的Rabi 振荡规律是吻合的,此时量子态不会发生衰减.图1(b)-(c),依次是位翻转误差(σx误差)、相位翻转误差(σz误差)、混合型误差(σy误差)、3 种平均误差等概率发生后子系统保真度随时间(t) 的演化.可以看出,各翻转类型下,保真度在最开始会发生较缓慢且差值不大的振荡变化;随着时间的增加,差值开始变小,振荡也趋于稳定;最终,保真度都会趋于稳定,不再发生变化.这或许可以说明,在开放环境的作用下,长时间的退相干后,量子态趋于形成一个较稳定的状态,此时保真度也降至最低.不同之处在于误差类型不同,稳定发生的时间也不同.可以看出,σy误差由于是两种误差的混合型,其对保真度的影响最为敏感和迅速;而3 种误差等概率发生的影响介于三者之间,可以认为是三者的平均结果.

另外,对一种误差翻转情形取P为不同值,观察不同翻转概率时保真度振幅的差异.在3 种误差等概率翻转下,对式(12)—(15)取P=0.2,0.5,0.7,1,不同概率下保真度的对比详见图2.

图2 不同概率下保真度的对比Fig.2 Comparison of fidelity at different probabilities

图2 所示是在3 种平均误差翻转情形下,翻转概率P取不同数值时保真度随时间(t) 的变化.可以发现,由于翻转的发生,保真度会发生振荡变化,随着时间演化,最后会逐渐在固定值处趋于稳定;而随着翻转概率的增大,最后处于稳定的时间也在变短,稳定值也越来越小;当发生完全翻转时,量子态的保真度也逐渐趋近于零,量子信息发生全部失真.

基于上述的多种情形,本文发现,子系统一旦暴露于开放环境,信息不可避免会发生失真情况,并且存在不同的误差翻转对保真度的影响也并不相同;随着时间演化,存在退相干的演化对比非退相干演化,保真度也会发生周期衰退直至形成系统信息失真形成稳定情况;另外,随着误差翻转概率的增加,量子信息失真程度也会越来越严重.

3 退相干情况下von Neumann 熵变化

von Neumann 熵(Sv-N) 的表达式为

式(16)中:ρ表示量子态的约化密度矩阵;λα表示此时密度矩阵对应的本征值.

本文在类比保真度的推导过程中,将末态密度矩阵代入,求出von Neumann 熵的值;使用Matlab 工具做出退极化模式下的von Neumann 熵的变化图,并进行对比分析.

在退极化模式下,分别单独考虑σx误差、σz误差、σy误差以概率P翻转,以及3 种误差等概率的情形.类比第2 章保真度的计算,求得其熵的表达式.

将式(9)、式(11)—(15)代入式(16),取P=0.2,von Neumann 熵的对比详见图3.

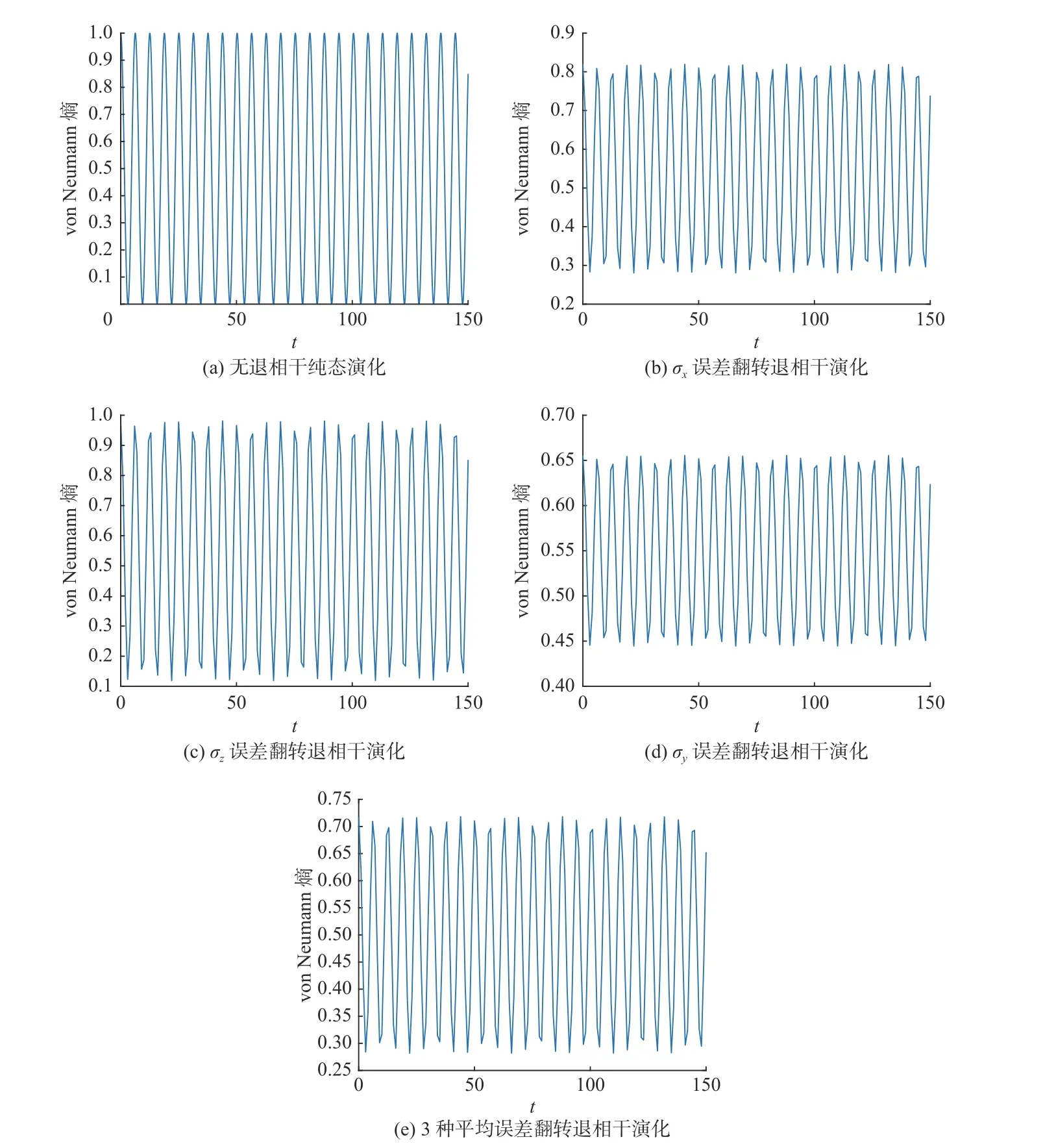
图3 von Neumann 熵对比Fig.3 von Neumann entropy comparison

图3 所示是非退相干演化与退相干演化后的von Neumann 熵随时间演化的拟合图像.图3(a)是无退相干的纯态演化,此时由于时间演化算符中含有时间因数,末态的von Neumann 熵会随着时间演化产生有规律的振荡.图3(b)—(e)依次是位翻转误差(σx误差)、相位翻转误差(σz误差)、混合型误差(σy误差),以及以上3 种误差等概率发生后子系统von Neumann 熵随时间的演化.可以看出,存在退相干时与无退相干时von Neumann 熵的振荡范围是不同的: 无退相干时,von Neumann 熵的值在 0～1 间振荡;存在退相干时,各翻转类型下不同振荡的高低范围也不尽相同.这或许可以说明,在开放环境下[13-16],发生一次退相干后,由于时间因数的存在,von Neumann 熵会发生振荡变化,此时系统的有序性也在变化.还可以看出,σy误差由于是两种误差的混合型,其对von Neumann 熵的影响最为敏感和迅速,而3 种误差等概率发生的影响介于三者之间,可以认为是三者的平均结果.

由上述结果可以发现,随着时间演化,存在退相干的演化对比非退相干演化,von Neumann 熵振荡振幅并不相同,存在误差翻转时振荡振幅也各有不同,但仍保持振荡并不会衰减至某一稳定值.这代表系统的混乱程度在发生变化,量子态之间的关联程度也在变化,但是仍存在一定的关联性.

上述各误差翻转中,von Neumann 熵的变化有增亦有减的趋势,似乎违背热力学统计物理中“熵增原理”的说法.但是本文所研究的演化过程与经典力学所遵循的熵增原理是不同的,在量子理论中,熵的变化仅能使人们对体系的混乱程度的变化有所了解,体系可以从无序到有序,那么也可以从有序到无序.

4 总结

本文使用Kraus 求和方法,对于退极化模式下末态演化的保真度与von Neumann 熵的变化进行了分析,使用Matlab 工具做出了变化的拟合图像.发现二能级原子与单模光场相互作用体系[17]在误差翻转的情况下,量子态会发生退相干效应[18],其中,退极化模式下3 种误差翻转对保真度与von Neumann 熵变化的影响不尽相同,相同之处在于,存在退相干时量子态的保真度与von Neumann 熵不会再保持 0～1 之间的振荡,而是会发生部分信息的失散,体系关联度也在下降,振荡范围发生改变;不同之处在于,保真度会随着时间衰退至慢慢稳定,而von Neumann 熵始终保持振荡,这与二者的物理性质有关.