哈密顿量宇称-时间对称性的刻画*

张慧洁 贺衎

(太原理工大学数学学院,太原 030024)

宇称-时间(PT)对称性理论描述了具有实能级的非厄密特哈密顿量,在量子物理学和量子信息科学中起着重要作用,是量子力学中活跃且重要的主题.研究者们对如何描述哈密顿量的PT 对称性的问题给予了高度关注.本文基于PT 对称理论和哈密顿量归一化特征函数,提出了算子F 的定义.然后,在找到算子CPT和算子F 的对易子和反对易子的特性后,给出了刻画了无量纲情况下哈密顿量的PT 对称性的第一种方法.进一步研究发现,该方法还可以量化哈密顿量在无量纲情况下的PT 对称性.此外,提出了另一种基于哈密顿量特征值实部和虚部来描述哈密顿量PT 对称性的方法,该方法仅用于判断哈密顿量是否具有PT 对称性.

1 引言

量子力学中的一个重要理论是宇称-时间(PT)对称理论.PT 对称理论的研究始于量子力学模型的研究.量子力学是数学希尔伯特空间中的态与实验中可测概率间的联系.由于概率是实的且是正的,所以要求概率所对应的希尔伯特空间上的向量的范数必须是正的.由于概率是守恒的,是不随时间变化的,即时间酉演化,所以希尔伯特空间上的任意两个不同向量之间的内积在时间上必须是常数.所以有了量子力学中任何量子理论都不能违背的两个基本公理: 1)能级是实的;2)时间酉演化.想要满足量子力学的两个基本公理需要限制数学上的哈密顿量是实的、对称的,但这不是一般的条件.事实上,物理情形中存在复哈密顿量,许多研究者将哈密顿量H从实空间推广到了复空间[1],这就有了更一般的条件要求: 哈密顿量是厄密的.

1998年,Bender 和Boettcher[2]发现具有实谱的非厄密哈密顿量具有PT 对称性.后来Bender[3]指出,因为函数PT 对称,所以考虑哈密顿量H=+是PT 对称的.通过考虑哈密顿量H=+的δ 展开H=,发现加入微小摄动的哈密顿量的能级在δ≥0时,哈密顿量的能级仍然是实的[4],所以引入了PT对称理论来描述有实能级的非厄密的复哈密顿量.拥有实能级的复哈密顿量可以是PT 对称的哈密顿量,也可以是厄密的哈密顿量,但是不能同时都是.但是实哈密顿量可以既是PT 对称的哈密顿量,又是厄密的哈密顿量.实际上,早已有文献说明非厄密PT 对称哈密顿量已经被用来描述小球量子系统的基态、场理论和Lee-Yang 边缘奇点等现象[5–7].文献[2]描述了PT 对称理论中新的复哈密顿量不同于经典的和量子的性质,刻画了非厄密哈密顿量的能级谱.文献[8]说明PT 对称的哈密顿量的能级谱仍然满足量子力学的两个公理,可以把PT 对称量子力学视为普通量子力学的复杂版本.

关于PT 对称理论及其应用的研究也不断深入[9−11].文献[9]研究了PT 对称耦合振子中的二重跃迁.文献[10]讨论了PT 对称哈密顿量在量子信息科学中的应用.利用PT 对称哈密顿量的不等价实验解决了使用PT 对称哈密顿量执行指数级快速数据库搜索(量子计算机不可能完成)与超光速信息传递的不可能性以及局域操作下纠缠的不变性等基本信息原理之间的冲突.充分评估了使用PT 对称哈密顿量提出的更快的时间演化和状态识别的方案.文献[11]利用PT 对称理论的非线性性质,说明在PT 对称性下,增益和损耗可以为波导系统提供最佳的和灵活的控制.这使得PT 对称性可能有很多物理上的应用,如光开关、单向无反射PT-光学频率下的对称超材料、单模PT 对称微环激光器、CPA 激光器和声子激光器等.

对于哈密顿量的PT 对称性的刻画同样值得进一步的研究.2018年,El-Ganainy 等[12]关注了非厄密物理学和PT 对称性间得与失的相互作用导致的新特征.2020年,Pi 等[13]说明了复Berry相拓扑结构和PT 对称破缺之间的关系.同年,俞上等[14]提出了一种基于扩张哈密顿量的弱测量来表征哈密顿量的PT 对称性的理论和实验方法,该方法也可以用来判断哈密顿量H是否PT 对称.

本文给出了哈密顿量PT 对称性理论上的其他刻画方式,主要结构如下: 第1 节介绍本文用到的一些基础知识;第2 节基于PT 对称理论,定义与哈密顿量归一化特征函数相关的算子F,刻画并量化哈密顿量的PT 对称性;第3 节通过使用哈密顿量能级的实部和虚部,利用已定义算子F,给出判断哈密顿量PT 对称性的另一种方法;第4 节总结本文的研究内容.

2 基本理论

1) 对易子和反对易子[15]

对易子:[A,B]=AB-BA.

反对易子:{A,B}=AB+BA.

对易子与反对易子通常与一对算子的可交换性和不可交换性相关,也与算子的对称性与不可对称性有关,可以作为研究量子力学问题时的工具.

2) 给定无量纲哈密顿量的参数范围下的能级情况[2,16]

哈密顿量H的形式:

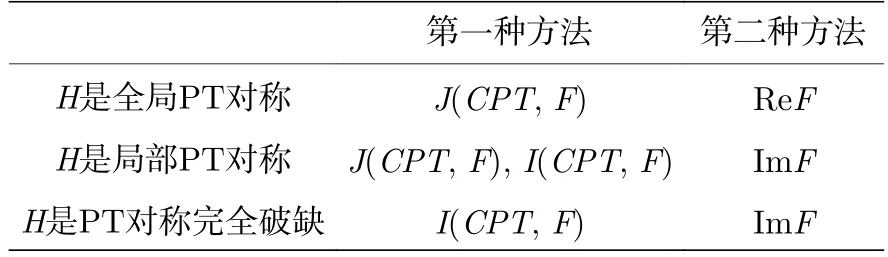
其中N是实数(N>0),m不等于0,和分别是动量运算符和位置运算符(在本文中,可以将,视为无量纲).有哈密顿量H的一般谱: 哈密顿量H的能级是参数N的函数.值得注意的是: 当N≥2时,能级谱是正的也是实的;N=2 对应于谐振子,其能级为En=2n+1;当1

3) 量子力学的两个公理: 能级是实的;时间酉演化.

4) PT 对称理论[3]

PT 对称理论核心的想法是用哈密顿量具有时空反演对称性(PT 对称性)这个较弱的条件代替量子理论中厄密的哈密顿量.用PT 对称性代替厄密性条件时,如果哈密顿量的对称性没有被打破,哈密顿量将表现出厄密哈密顿量描述的所有量子特征.而且PT 对称的哈密顿量有和PT 算子可交换的性质,即有[H,PT]=0 .PT 对称的哈密顿量在时间反演算子T对时间的反演(p →-p,x →-x,i→-i)和宇称算子P对于空间的反转(p →-p,x →-x)的共同作用下是不变的.但是哈密顿量H既不在宇称算子P下不变,也不在时间反演算子T下不变.因此对于PT 对称的哈密顿量H,有H=HPT=PTH.

5) 狄拉克δ 函数[17]

为了表示物理学中的质点、点电荷、瞬时力等不连续分布于空间或时间中,而是集中在空间的某一点或时间的某一瞬时的抽象模型的密度分布引入的概念.数学表示为δ(x)=0,(x0),=1.该表达式规定函数在0 点取非零值,其他点取0 值.不规定δ 函数在0 点的大小,函数值的大小由第二个积分式决定.

6) 本文所用名词解释

完全PT 对称的哈密顿量: PT 对称不破缺的哈密顿量,特征值全部为实特征值,整体随时间做酉演化.

局部PT 对称的哈密顿量: PT 对称破缺的哈密顿量,特征值为实特征值和复特征值对,整体随时间做非酉演化,局部随时间做酉演化.

PT 非对称的哈密顿量: PT 对称完全破缺的哈密顿量,没有实特征值,只有复特征值对.

哈密顿量的局部PT 对称部分: PT 对称破缺的哈密顿量保持PT 对称的部分,具有实特征值,这些实特征值是哈密顿量特征值的一部分.哈密顿量的PT 对称部分随时间做酉演化.

哈密顿量的PT 对称破缺部分: PT 对称破缺的哈密顿量不保持PT 对称的部分,具有复特征值对,这些复特征值对是哈密顿量特征值的一部分.不保持PT 对称的部分随时间做非酉演化.

3 利用对易子和反对易子刻画哈密顿量的PT 对称性

本节利用对易子和反对易子,进一步研究无量纲的哈密顿量的PT 对称性.虽然可对角化和非可对角化哈密尔顿量都可以定义具有正CPT范数的希尔伯特空间,但是只有可对角化哈密顿量的特征函数是其退化根子空间的基函数,而非可对角化哈密顿量对应于退化根子空间的基函数不是哈密顿量的本征函数[16].哈密顿量非可对角化的情况比较复杂,所以为了便于研究,需要确保哈密顿量是可对角化的.又由于正则斯图姆-刘维尔问题的证明结果,特征行列式中不存在多个零点[18]时,哈密顿量H的特征函数在希尔伯特空间中是完备的.因此,本节的研究基于系统的理想假设: 系统中不存在零CTP范数,即特征行列式中不存在多个零点.所以本节研究的哈密顿量是可对角化的,且其特征函数在希尔伯特空间中是完备的.

3.1 重构宇称算子P,哈密顿量H 的空间表示

设ψn是与哈密顿量H的特征值En相对应的特征函数,ϕn是哈密顿量H的归一化特征函数.这意味着:

为了更清晰地表征,可以根据本征函数重构宇称算子P、哈密顿量H的空间表示,分别表示如下[3]:

宇称算子P是酉的:P2=1.且有Hϕn(x)=Enϕn(x),En是哈密顿量H的能级.

特别地,Hϕn可以被表示为:Hϕn=Enϕn=Anϕn+Bniϕn(An+Bni=En),ϕn是能级En所对应的本征函数.An和Bn是实数,表示能级En的实部和虚部.

厄密量子力学中,希尔伯特空间内积是具体的[3].对于非厄密的哈密顿量,对PT 空间上的两个函数f(x)和g(x) 的内积的合理猜测是

这里,PTf(x)=[f(-x)]∗,有f(x)的PT范数为

所以哈密顿量H的本征函数ϕm(x)和ϕn(x)有新的内积形式.然而,本征函数的PT范数不是正定的:(ϕm,ϕn)=(-1)nδmn,当m=n.这是因为在PT 对称量子力学中,量子态的矢量空间是由能量本征函数构造的,其中一半有范数 +1,另一半有范数-1[3].

3.2 引入线性算子C

在连续对称理论中,哈密顿量H的对称性与正负能级的数量有关.这不利于描述哈密顿量H的局部PT 对称和破缺部分.为了便于描述哈密顿量H的局部PT 对称和破缺部分,引入了线性算子C.其性质类似于量子场论中的电荷共轭算符.还可以根据本征函数重构线性算子C,其空间表示如下:

线性算 子C是酉的:C2=1,且特征值是±1,C表示本征函数ϕn(x)的PT范数的符号的测量.因为C是线性算子,所以有Cϕn(x)=(-1)nϕn(x) .线性算子C具有一般的算子表示形式[3]:

则有

其中,An+Bni=En;An和Bn是实数,分别是能量级En的实部和虚部[3].

令K 是一个基于哈密顿量H的本征函数的空间,可以在空间 K 上得到函数f的CPT范数[3,19],如下所示:

其中CPTf(x)=.此内积满足正范数的要求和量子力学中的酉理论.

3.3 定义与哈密顿量归一化特征函数有关的算子F

算子G是将复空间中哈密顿量H的特征函数ϕn与其对应能级En的乘积作为列向量的算子.可以表示为

由CPT算子和哈密顿量H的空间重构,如果ϕn属于局部PT 对称部分,则CPTϕn(x)=[ϕn(-x)]∗=ϕn(x),且能级En是实的,所以CPTHϕn(x)=[ϕn(-x)]∗=Enϕn(x),否则,CPTHϕn(x)=[ϕn(-x)]∗[3].

若ϕn(n=1,2,···,n,···) 属于哈密顿量局部PT 对称部分,当m=n时,有(ϕn(x),ϕm(x))=若存在ϕn(n=1,2,···,n,···) 不属于哈密顿量局部PT 对称部分,则有上式中的不等号.

令cn=En/∥G∥,an=An/∥G∥,及bn=Bn/∥G∥,则算子G归一化得到算子F:

由CPT算子和哈密顿量H的空间重构,得到

所以,算子F的CPT 范数为

3.4 刻画哈密顿量的PT 对称性

将PTF分为两部分:PTF=[PT,F]+{PT,F}.其中[3],

对易算子[PT,F]表示PT和F是不可交换,反对易算子{PT,F}表示PT和F是可交换的.

又因为CPT算子是酉的,所以

接下来,将得到∥{CPT,F}∥CPT和∥[CPT,F]∥CPT的界.

因为CPT算子是酉的,CPT2=I,所以

因为ϕn不总是属于局部PT 对称的部分,函数f不一定是完全PT 对称的,所以f和CPTf不能保证是时间酉演化的.由于CPT算子是酉的,CPT-1算子也是酉的,所以

其中,∥∗∥a是算子范数.

这表明,0 ≤∥[CPT,F]∥CPT≤1/2 .

这意味着:

根据I(CPT,F),J(CPT,F) 的范围和与交换性的联系的特性,则有:

I(CPT,F)=∥[CPT,F]∥CPT可以表示PT 对称破缺部分;

J(CPT,F)=∥{CPT,F}∥CPT可以表示PT对称部分.

若I(CPT,F)=∥[CPT,F]∥CPT=0,表示所有ϕn属于PT 对称部分,即哈密顿量H是全局PT对称的.

若I(CPT,F)=∥[CPT,F]∥CPT0,表明ϕn属于PT 对称破缺部分,即哈密顿量H是PT 对称破缺的.

可以得到如下结论:

1)当N<1,哈密顿量H的能级谱中没有实特征值,不满足量子力学的两个公理.此时哈密顿量H是PT 对称完全破缺的,可以用I(CPT,F)=∥[CPT,F]∥CPT表示.

2)当1

3)对于N≥2,哈密顿量H的能级谱的特征值都是正的实特征值,哈密顿量H是全局PT 对称的,可以用J(CPT,F)=∥{CPT,F}∥CPT表示.

这意味着I(CPT,F)和J(CPT,F) 是守恒的,且当F为全局PT 对称的取最后一个等号,这与哈密顿量H的破缺部分和PT 对称部分是守恒的相一致.

基于上述讨论,建立了描述哈密顿量H的PT 对称性的一种方式.该方法下,哈密顿量H的局部PT 对称性与哈密顿量H与CPT算子的可交换性有关,哈密顿量H的破缺部分与哈密顿量H与CPT算子的不可交换性有关.该方法可以量化哈密顿量H的局部PT 对称部分和破缺部分,而不是仅仅判断哈密顿量H是否是全局PT 对称的.对于给定的哈密顿量H,可以得到特征值En和相应的特征函数ϕn,以及算子F的定义,进而得到哈密顿量H的PT 对称部分和破缺部分.

4 利用哈密顿量特征值的实部和虚部判断哈密顿量的PT 对称性

对于仅仅需要区分哈密顿量H是否是全局PT对称的情况,本节给出另一种较为简捷的刻画方式.该方法同样基于上述定义中的算子F,通过利用哈密顿量H的实部和虚部,刻画哈密顿量H的PT 对称性.

4.1 利用CPT 算子和F 算子表示哈密顿量的实部和虚部

本节定义另外一组特殊的算子,使其CPT范数为上一节算子F的实部ReF和虚部ImF的倍数.由算子F和哈密顿量H归一化特征函数的密切关系可以反映出哈密顿量H的实部或者虚部的情况.

另一方面,

所以,

表明算子F的实部和虚部的和是守恒的.这与确定的哈密顿量H的实部和虚部是守恒的相一致.

4.2 判断哈密顿量的PT 对称性

若ImF=0,所有本征函数ϕn的能级En仅有实部,是实数.此时全部本征函数ϕn属于PT 对称部分,表明哈密顿量H是全局PT 对称的,反之亦然.若ImF0,表明存在本征函数ϕn的能级En是具有虚部的,是复数.表明此时的哈密顿量H是PT 对称破缺的,反之亦然.若ReF=0,所有ϕn的能级En只有虚部,ϕn必定属于PT 对称完全破缺的部分,表明哈密顿量H是PT 非对称的,反之不然,是充分不必要条件.

5 结论

本文给出了刻画哈密顿量H的PT 对称性的两种方式: 1)J(CPT,F),I(CPT,F) ;2)ReF,ImF.由于实数和虚数在实验上是可探测的,后者比前者可能更容易操作.若仅关注哈密顿量H是否是PT 对称破缺的,而不关注破缺部分的量化,使用ImF的刻画方式更简捷.但前者在理论上可能更好,因为使用J(CPT,F) 可以量化哈密顿量的局部PT 对称部分,而ReF不能用于量化哈密顿量的局部PT 对称部分.

若哈密顿量H是全局PT 对称的,只需要关注实部ReF和PT 对称部分J(CPT,F) .若哈密顿量H是PT 对称破缺的,而第二种刻画方式只需要关注ImF,对于第一种刻画方式需要关注局域PT 对称部分J(CPT,F) 和PT 对称破 缺部分I(CPT,F).若哈密顿量H是完全破缺的,可以仅关注ImF和PT 对称破缺部分I(CPT,F),如表1所列.

表1 比较刻画哈密顿量H PT 对称性的两种方法Table 1.Compare two depiction methods of PT-symmetry of Hamiltonian H.

需要注意的是,当想要判断哈密顿量H是否是完全PT 对称破缺时,需要关注I(CPT,F) 是否为0,而不是ReF是否为0,因为ReF不利于区分局部PT 对称性和PT 对称完全破缺性.若哈密顿量H是PT 非对称的,则存在哈密顿量H的本征函数ϕn的能级En是复数,但不一定是纯虚数,所以ReF不一定为0.由于参数N与哈密顿量H能级谱的关联,此区别主要体现于参数N≤1 的情形.