识别高阶网络传播中最有影响力的节点*
李江 刘影2) 王伟 周涛
1) (西南石油大学计算机科学学院,成都 610500)
2) (弗里堡大学物理系,弗里堡 1700)
3) (重庆医科大学公共卫生学院,重庆 400016)
4) (电子科技大学大数据研究中心,成都 611731)
识别网络传播中最有影响力的节点是控制传播速度和范围的重要步骤,有助于加速有益信息扩散,抑制流行病、谣言和虚假信息的传播等.已有研究主要基于描述点对交互的低阶复杂网络.然而,现实中个体间的交互不仅发生在点对之间,也发生在3 个及以上节点形成的群体中.群体交互可利用高阶网络来刻画,如单纯复形与超图.本文研究单纯复形上最有影响力的传播者识别方法.首先,提出单纯复形上易感-感染-恢复(SIR)微观马尔可夫链方程组,定量刻画单纯复形上的疾病传播动力学.接下来利用微观马尔可夫链方程组计算传播动力学中节点被感染的概率.基于网络结构与传播过程,定义节点的传播中心性,用于排序节点传播影响力.在两类合成单纯复形与4 个真实单纯复形上的仿真结果表明,相比于现有高阶网络中心性和复杂网络中最优的中心性指标,本文提出的传播中心性能更准确地识别高阶网络中最有影响力的传播者.
1 引言
现实世界中,许多具有扩散效应但仅由局部相互作用驱动的动力学过程可以用复杂网络上的传播来描述,如社交网络上的流行病与谣言传播[1,2]、电力网络上电站的级联失效[3]、交通网络上的道路阻塞[4]、计算机网络上的病毒传播[5]等.失控的传播可能对社会经济及人们生活造成大范围的负面影响,如COVID-19 大流行影响经济发展[6],谣言传播引起民众恐慌[7],电力网络中部分设备故障导致电网瘫痪[8].由于网络结构的异质性,网络中节点的传播影响力具有显著的差异[9].如在Twitter与Facebook 平台仅有少量账户的信息被广泛分享[10],COVID-19 中10%最具传染性的宿主导致近80%的感染[11].网络传播中影响力最大的节点被称为最有影响力的传播者.识别最有影响力的传播者是快速、有效地控制传播过程的关键步骤.节点中心性利用网络拓扑结构度量节点在网络中的重要性.如基于邻居数目的度中心性[12]、H-index 中心性[13]、k 壳中心性[14]、集体影响中心性[15]等,基于路径的接近中心性[16]、介数中心性[17]、子图中心性[18]以及基于特定动力学过程迭代稳态的指标,如特征向量中心性[19]、PageRank[20]、非回溯中心性[21]等.随后,大量基于中心性的方法被提出,识别网络中最有影响力的传播者的算法性能不断提升,并从单层网络推广到多层网络[22–28].
已有识别最有影响力传播者的研究主要针对描述节点间成对关系的简单网络.简单网络用节点表示个体,边表示两个节点间的交互.然而现实中许多系统存在超越点对的成组交互,例如学术论文通常由团队共同完成[29],谣言与思想的传播在小范围群体中被加强[30].由3 个及以上个体组成的群体交互被定义为高阶交互,单纯复形和超图是两种描述高阶交互的数学工具[31].单纯复形是由一系列单纯形组成的集合.一个k阶单纯形由k+1个节点组成,且这些节点的任意节点子集也构成单纯形.如在科学家合作网中,若4 个作者组成一个3 阶单纯形,自然其中任意2 个作者,任意3 个作者也具有合作关系.在超图中,一条超边可包含任意数量的节点,表示这些节点相互影响.相比于单纯复形,超图不要求高阶交互的所有子交互必须出现在超图中.高阶网络上的传播动力学受到了广泛的关注.在高阶网络上的社会传播中,研究发现高阶结构会导致不连续相变与双稳态区域,双稳态区域中稳态规模依赖初始感染种子数目[30,32].在社会传播模型的基础上,研究人员提出了高阶网络上的多动力学耦合传播模型,例如高阶网络上的竞争传播与意识疾病耦合传播等.相比于简单图上的竞争传播[33],引入高阶交互使两种流行病可共存[34].意识疾病耦合传播中,社交网络中的高阶交互可缓解低流行病传播率下信息传播不足的问题,有助于抑制流行病传播[35].
简单网络与高阶网络间的传播现象具有明显差异,因此识别高阶网络上最有影响力传播者的研究值得关注.度中心性、接近中心性、介数中心性和特征向量中心性等概念被扩展至单纯复形,用于识别核心蛋白[36].类似地,特征向量中心性被推广并应用于识别超图中的重要节点与重要超边,其主要思想为节点的重要性依赖于节点参与超边的重要性,而超边的重要性依赖超边所包含节点的重要性[37].还有研究人员提出向量中心性以描述节点在不同尺寸超边中的重要性[38].现有高阶网络中重要节点识别方法主要基于网络结构,鲜有同时考虑网络结构与传播过程.
已有研究表明节点的传播影响力由网络拓扑结构与传播过程共同决定.相比于仅使用网络拓扑结构的方法,同时考虑传播过程与网络拓扑结构的方法能更准确地识别网络传播中最有影响力的传播者[39,40].本文基于网络结构与传播过程,提出传播中心性.首先提出单纯复形上易感-感染-恢复(susceptible-infected-recovered,SIR)微观马尔可夫链方程组用于描述单纯复形上的SIR 传播动力学;接下来计算微观马尔可夫链方程组收敛时节点被感染的概率.节点被感染的概率由网络结构与传播过程共同决定,将其定义为 “传播中心性” (spreading centrality,SC),用于排序节点的传播影响力.在两类合成网络与4 个真实网络上的大规模仿真实验表明,传播中心性与节点真实传播影响力高度正相关.相比于高阶网络的度中心性、特征向量中心性以及简单网络上最优的集体影响中心性、非回溯中心性等基准中心性,本文提出的传播中心性能更为准确地识别高阶SIR 传播中最有影响力的节点,排序准确性更高.
2 单纯复形上的传播模型
本节首先介绍单纯复形的定义,再说明单纯复形上的易感-感染-恢复传播模型.单纯复形定义为M=(V,C),其中,V表示节点集合,C表示单纯形集合[30].k阶单纯形σ ⊂C表示k+1 个节点{v0,v1,v2,···,vk}组成的高阶交互.单纯复形中,0 阶单纯形表示单个节点,1 阶单纯形表示边,2 阶单纯形表示“满”三角面等.单纯复形满足以下条件,若单纯形ω ⊂C,其所有子单纯形v ⊂ω必须被包含在C中.如2 阶单纯形w={v0,v1,v2}⊂C,则{v0},{v1},{v2},{v0,v1},{v0,v2}和{v1,v2}⊂C.为了简便,使用的单纯复形中仅包含0 阶单纯形(节点),1 阶单纯形(边)和2 阶单纯形(高阶交互).
在单纯复形上的SIR 传播[41]中,个体可有3 种状态: 易感态(susceptible,S),感染态(infected,I),或恢复态(recovered,R).在每个时间步,I 态个体以一定速率将S 态邻居感染,并以一定速率自发恢复为R 态.单纯复形上,沿着1 阶单纯形(连边)和2 阶单纯形(三角面)都将发生感染事件.本模型的传播参数为(β1,β2,µ),其中β1表示1 阶单纯形感染S 态成员的速率,β2表示2 阶单纯形感染S 态成员的速率,μ表示I 态个体的恢复速率.图1展示单纯复形上个体感染与恢复的过程,边表示1 阶单纯形,“满”三角面表示2 阶单纯形.图1(a)—(j)中橙色边表示S 态个体通过1 阶单纯形以速率β1被感染.图1(h)中橙色“满”三角面表示S 态个体通过2 阶单纯形以速率β2被感染.图1(h)中,S 态个体不仅通过1 阶单纯形被感染,同时也通过2 阶单纯形被感染.注意,当且仅当2 阶单纯形中的两个节点同时处于感染态时,2 阶单纯形才能感染其第3 个成员.图1(j)中,3 个节点虽形成“满”三角面,但其中只有1 个节点感染,流行病无法通过2 阶单纯形进行传播.
3 传播中心性
本节提出单纯复形上的微观马尔可夫链方程组,通过微观马尔可夫链方程组计算动力学稳态时各节点被感染的概率,并将其定义为节点的传播中心性.定义为t时刻节点i处于X状态的概率,X ∈{S,I,R},如表示t时刻节点i处于S 态的概率.定义qi(t) 表示t时刻节点i没有被1 阶单纯形感染的概率,有
其中,Γi表示包含节点i的1 阶单纯形集合.定义表示t时刻节点i没有被2 阶单纯形感染的概率,有
其中,∆i表示包含节点i的2 阶单纯形集合.节点i在t时刻未被感染的概率qi(t) 可定义为
节点i处于不同状态概率随时间t的演化方程组可写为
(4)式表示节点i在t时刻处于S 态且未被感染,在t+1 时刻仍处于S 态的概率.(5)式右边第1 项表示节点i在t时刻处于S 态且被感染,在t+1 时刻处于I 态的概率.右边第2 项表示节点i在t时刻处于I 态且未恢复,在t+1 时刻仍处于I 态的概率.(6)式由节点处于S态,I 态与R 态的概率之和为1 的性质所得.
为了求解单个节点作为初始传播源时,系统达到稳态后各节点被感染的概率,初始时设置=1-1/N,=1/N,=0,N为网络中节点数目.迭代(1)—(6)式至收敛,获得各节点被感染概率.将其定义为传播中心性(spreading centrality,SC).流行病通过接触传播,疾病将优先到达拥有着更多接触的个体,即表现出更高的被感染概率.一旦这些个体被感染,他们更有可能将流行病传播出去,造成大规模感染.传播中心性属于迭代中心性,但与特征向量中心性等不考虑传播过程的迭代中心性不同,传播中心性加入了传播过程,迭代过程与传播过程一致.
4 仿真实验方法
为了验证传播中心性识别最有影响力传播者的准确性,我们在两类合成网络(匀质度分布网络与异质度分布网络)与4 个真实网络上进行大量仿真实验.本节首先介绍合成网络与4 个真实网络的生成方法,然后说明4 个用于比较的基准中心性及评价准确性的指标.
4.1 网络构建方法
在实验中使用了随机单纯复形与无标度单纯复形两种合成网络.随机单纯复形模型(random simplicial complex,RSC)用于生成匀质度分布的单纯复形[42].生成步骤如下: 以概率p1在任意两节点间生成边,再以概率p2在任意3 个节点间生成2 阶单纯形.p1,p2与节点平均关联的1 阶单纯形数目〈k1〉,节点平均关联的2 阶单纯形数目〈k2〉 之间关系如下:
无标度单纯复形模型(scale-free simplicial complex,SFSC)用于生成异质度分布网络[42].生成步骤如下: 以Barabási-Albert 模型生成无标度网络,即每个新加节点按度偏好选择m个旧节点生成连边.然后以概率p2在任意3 个节点间生成2 阶单纯形.〈k2〉可由(8)式计算,〈k1〉 表示为
采用4 个面对面接触数据集构建真实单纯复形[43–46].这些数据集从不同的人群接触场所中得到,包括工作场所(InVS15)、医院(LH10)、会议(SFHH)与高中(Thiers13).每个数据集中,记录了以20 s 为时间间隔的个体间面对面的交互.我们以5 min 作为时间窗口聚合数据.在一个时间窗口中,若两个节点有面对面接触则生成一条边,即1 阶单纯形.3 个节点两两接触则生成2 阶单纯形.统计边与2 阶单纯形在所有时间窗口中出现的总次数,最后保留50%出现次数最多的1 阶单纯形与20%出现次数最多的2 阶单纯形用于构建真实单纯复形.表1 展示了使用上述方法构建的合成单纯复形与真实单纯复形的简单统计特征,其中N为网络中节点数目,〈k1〉 为节点平均关联的1 阶单纯形数目,〈k2〉 为节点平均关联的2 阶单纯形数目,是流行病爆发时,1 阶单纯形传播速率的阈值,通过计算机模拟所得.在后文实验中,将1 阶单纯形传播速率设置为该模拟阈值的1—2倍,以控制传播规模.

表1 合成与真实单纯复形属性Table 1.Properties of the synthetic and real simplicial complexes.
4.2 基准中心性
为了与本文提出的传播中心性比较,我们选择高阶网络的度中心性[31]与特征向量中心性[37],简单网络上当前最优的集体影响中心性[15]与非回溯中心性[21]作为比较的基准中心性.
高阶网络上的度中心性定义为节点直接邻居数目或节点参与交互数目.本文采用节点交互数目的定义方式,则节点度中心性可写为
其中,ki表示节点i参与1 阶单纯形的数目,表示节点i参与2 阶单纯形的数目.
超图中节点与超边的特征向量中心性(EVH)认为节点重要性依赖于节点所在的超边,超边重要性依赖于超边所包含的节点,其数学定义为
式中,λ 和μ是比例常数.x,y是向量,xi表示节点i的特征向量中心性值,ye表示超边e的特征向量中心性值.B是超图的关联矩阵,超边e包含节点i,则Bie=1,反之Bie=0 .g,f,ψ,φ 是4 个映射函数,用于实现不同的依赖关系.本文中设定:
集体影响中心性(collective influence,CI)与非回溯中心性(nonbacktracking,NB)是简单网络上的最优中心性算法.集体影响中心性基于最优渗流,推导得出节点i的CI 中心性定义为
式中,ki表示节点i的度,∂Ball(i,l) 表示与节点i距离为l的节点集合.本文计算集体影响中心性时设置l=2 .
非回溯中心性与标准特征向量中心性类似,但通过非回溯矩阵避免标准特征向量中心性的局部化问题.节点j的非回溯中心性定义为
其中,A表示简单图的邻接矩阵,vi→j是简单图的非回溯矩阵的主特征向量中边ei→j对应的分量.将简单图上的集体影响中心性与非回溯中心性算法用于单纯复形时,我们不考虑单纯复形中的高阶交互(即“满”三角面)的影响,即仅考虑网络中的节点与连边.
4.3 评价指标
为了评估不同中心性识别最有影响力传播者的准确性,我们使用不准确函数[14]、肯德尔相关系数与Top-K准确率作为评价指标.不准确函数ξ(p)度量中心性识别最有影响力传播者的不准确性,定义为
其中p是计算节点的比例(0 ≤p≤1).M(p) 表示规模为N的网络中,中心性排序在前的pN个节点的平均传播影响力,Meff(p) 表示真实传播影响力排序在前的pN个节点的平均传播影响力.ξ(p) 量化了实际最有传播影响力的传播者与中心性最高的传播者间平均传播影响力的接近程度.ξ(p) 越小,中心性在识别最有影响力的传播者时越准确.
肯德尔相关系数用于度量两个排序序列的相关性,定义为
Top-K准确率用于度量中心性对最有传播影响力的前K个节点的识别准确性,定义为
其中,SK表示中心性值在前K的节点集合,表示真实传播影响力在前K的节点集合,|SK| 表示集合SK中的元素数目.Top-K准确率越高表示中心性识别最有传播影响力的节点越准确.
5 实验结果
我们在合成网络与真实网络上度量传播中心性SC 排序节点影响力的性能.首先,分析了节点传播中心性与传播影响力的相关性,如图2 所示.结果表明,节点传播中心性与传播影响力高度正相关.当β1=时,RSC 网络上节点传播中心性与传播影响力的皮尔逊相关系数为0.9691;当β1=时,皮尔逊相关系数分别为0.9887 与0.9910.其他网络上,结果与RSC 网络中类似.实验中,为了获得单个节点的传播影响力,对单纯复形上的SIR 传播模型进行大规模的蒙特卡罗模拟.初始时,将节点i设置为感染态,其余节点设置为易感态,统计传播达到稳态时网络的感染规模,即恢复态占比.独立重复上述模拟 103次,将感染规模的均值作为对节点i的真实传播影响力Si的估计.当系统初始状态确定时,微观马尔可夫链方程组的收敛状态是固定的,不具备随机性.我们设置(t=0)=1-1/N,(t=0)=1/N,(t=0)=0,通过迭代微观马尔可夫链方程组计算传播中心性.在实验中,固定恢复速率µ=1,通过改变传播速率β1与β2设定不同的有效传播速率.μ的取值仅影响传播的时间演化尺度,不影响实验结果.

图2 节点传播中心性与传播影响力的散点图.SC与S 分别表示归一化后的节点传播中心性与传播影响力(a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13Fig.2.Scatter plots of the spreaing centrality and spreaing influence of nodes.SC and S represent the normalized spreading centrality and spreading influence of nodes: (a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13.
为了考察提出的传播中心性SC 排序节点传播影响力的准确性,采用不准确函数作为评价指标.不准确函数值越低,该中心性识别最有影响力的传播者越准确.如图3 所示,传播中心性能准确有效地识别最有影响力的传播者.在所有网络上,传播中心性的不准确函数低于0.02,传播中心性多数情况下优于其他基准中心性.在SFSC 与Thiers13网络中,传播中心性明显优于所有基准中心性.在RSC 网络上,传播中心性略优于集体影响中心性、特征向量中心性与非回溯中心性,明显优于度中心性.在InVS15 网络中,当0
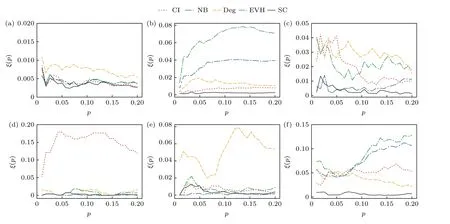
图3 各中心性的不准确函数(a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13 Fig.3.Imprecisions of the centralities: (a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13.
为了考察传播参数改变时,提出的传播中心性的性能,对比了不同1 阶单纯形传播速率下各中心性与节点传播影响力的相关性,如图4 所示.结果表明,在所有网络中,所提的传播中心性与传播影响力的肯德尔相关系数大于基准中心性与传播影响力的肯德尔相关系数.合成网络中传播中心性的肯德尔相关系数随1 阶单纯形传播速率的增大而增大.在RSC 网络中,传播中心性在1 ≤α≤1.4时略优于特征向量中心性、非回溯中心性和集体影响中心性,明显优于度中心性.当1.4<α≤2 时略优于集体影响中心性,明显优于其余中心性.SFSC网络中,传播中心性明显优于其他基准中心性.真实网络中结果与合成网络结果类似.在InVS15 与Thiers13 网络中,传播中心性明显优于其他基准中心性.在LH10 与SFHH 网络中,传播中心性略优于非回溯中心性,明显优于集体影响中心性,特征向量中心性与度中心性等基准中心性.其余传播参数设置如下: 恢复速率µ=1,1 阶单纯形传播速率β1=.2 阶单纯形传播速率设定为β2=0.1 .实验中设置1 阶单纯形传播速率β1∈.当β1<时,流行病不能爆发,所有节点的传播影响力接近于0;当β1>时,传播速率过大,所有节点都会导致较高的流行病爆发规模.传播速率过小或过大都无法充分地体现节点间传播影响力的差异.基本再生数度量感染节点感染下一代节点的能力,是传播中的一个重要参量.复杂网络SIR 传播模型基本再生数定义为R0=(k+s2/k)β/µ,其中β 是传播速率,μ是恢复速率,k是平均度,s是度分布的标准差.实验中,设置1 阶单纯形传播速率β1∈,此时各网络的基本再生数取值范围为: RSC [0.98,1.96];SFSC [1.06,2.12];InVS15[0.97,1.94];LH10 [0.97,1.94];SFHH [0.99,1.98];Thiers13 [1.05,2.10].由于流行病主要通过边进行传播,高阶作用仅起强化作用,我们计算R0时未考虑高阶作用.
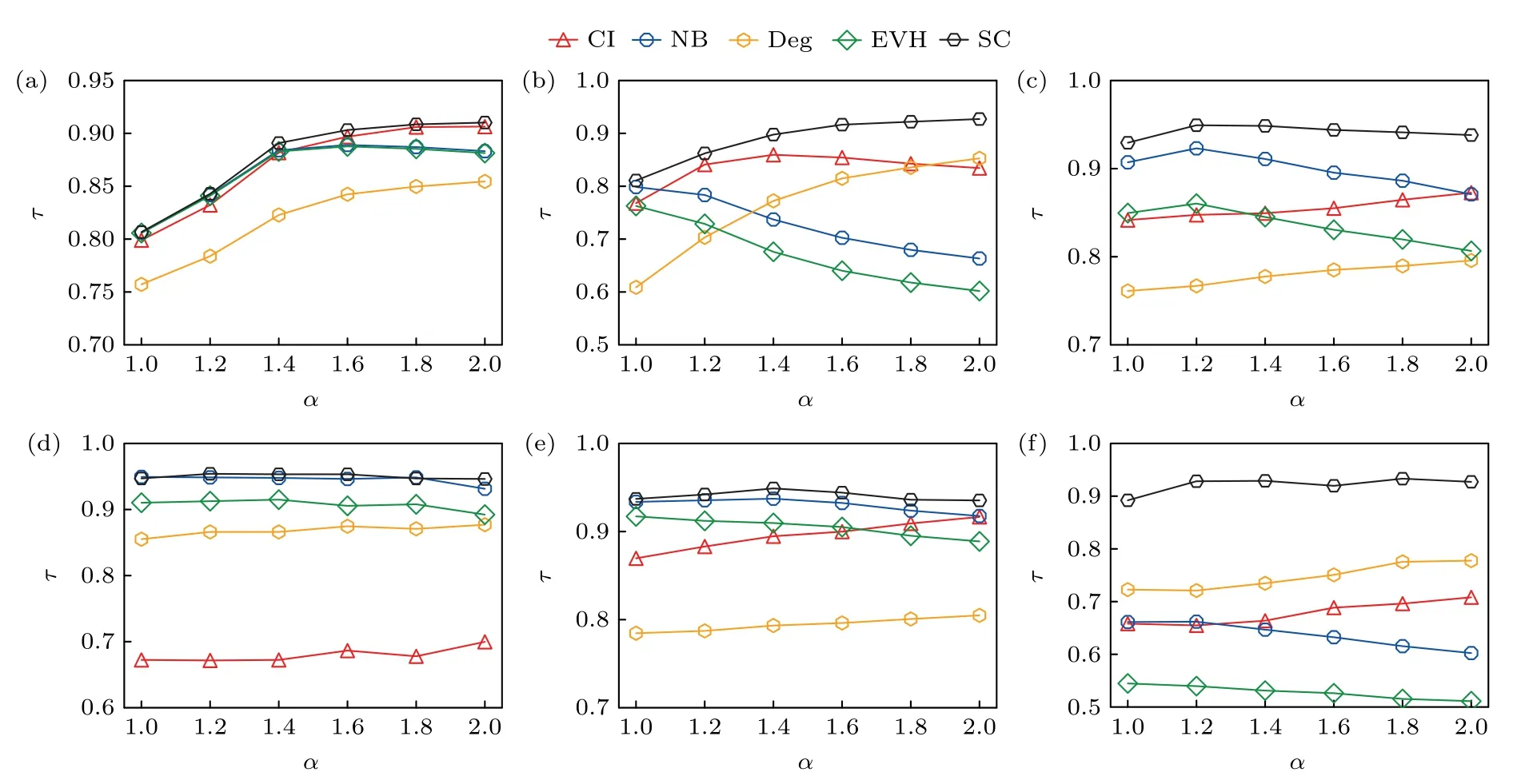
图4 不同1 阶单纯形传播速率 β1=下,节点各中心性与传播影响力的肯德尔相关系数(a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13Fig.4.Kendall’s tau correlation of the centralities and the spreading influence of nodes under different 1-simplex spreading rates β1=: (a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13.
在高阶网络传播中,2 阶单纯形传播速率会影响节点的传播影响力.我们改变2 阶单纯形传播速率β2,考察中心性与节点传播影响力的相关性.如图5 所示,在合成网络和真实网络中,多数情况下传播中心性SC 与节点传播影响力的相关性最高.在合成网络RSC 与SFSC中,传播中心性的肯德尔相关系数基本不随β2变化且优于基准中心性.在真实网络InVS15,LH10 与SFHH中,传播中心性的肯德尔相关系数随β2的增大呈现下降趋势.在Thiers13 中传播中心性的肯德尔相关系数变化趋势平坦.与基准中心性相比,InVS15 与Thiers13网络中传播中心性完全优于其他基准中心性.在LH10 网络中,当0 ≤β2≤0.1时,传播中心性优于所有基准中心性,当0.1<β2≤0.2 时传播中心性略差于非回溯中心性但优于其他基准中心性.SFHH网络结果与LH10 类似,当0≤β2<0.15 时传播中心性优于所有基准中心性,而当0.15≤β2≤0.2 时传播中心性略差于非回溯中心性但优于其他基准中心性.当β2=0时,2 阶单纯形不再传播流行病,高阶网络上的传播退回到普通网络上的SIR传播模型.此时,节点的传播中心性与传播影响力间的肯德尔系数接近或高于0.9,明显优于普通网络上性能最优的集体影响中心性与非回溯中心性.随着2 阶单纯形传播速率β2增大,传播中心性与传播影响力间的相关性呈现出小幅降低的现象.当传播发生在2 阶单纯形上时,节点感染与被感染过程是非对称的.若2 阶单纯形中仅有一个节点处于感染态,该单纯形无法传播流行病,即一个节点容易通过2 阶单纯形被感染不代表它容易通过2 阶单纯形传播流行病.随着2 阶传播速率β2增大,这种非对称性带来的负面效果将会升高,传播中心性与传播影响力间的相关性将小幅降低.在图5 的实验中,其余传播参数设置为:β1=,µ=1 .
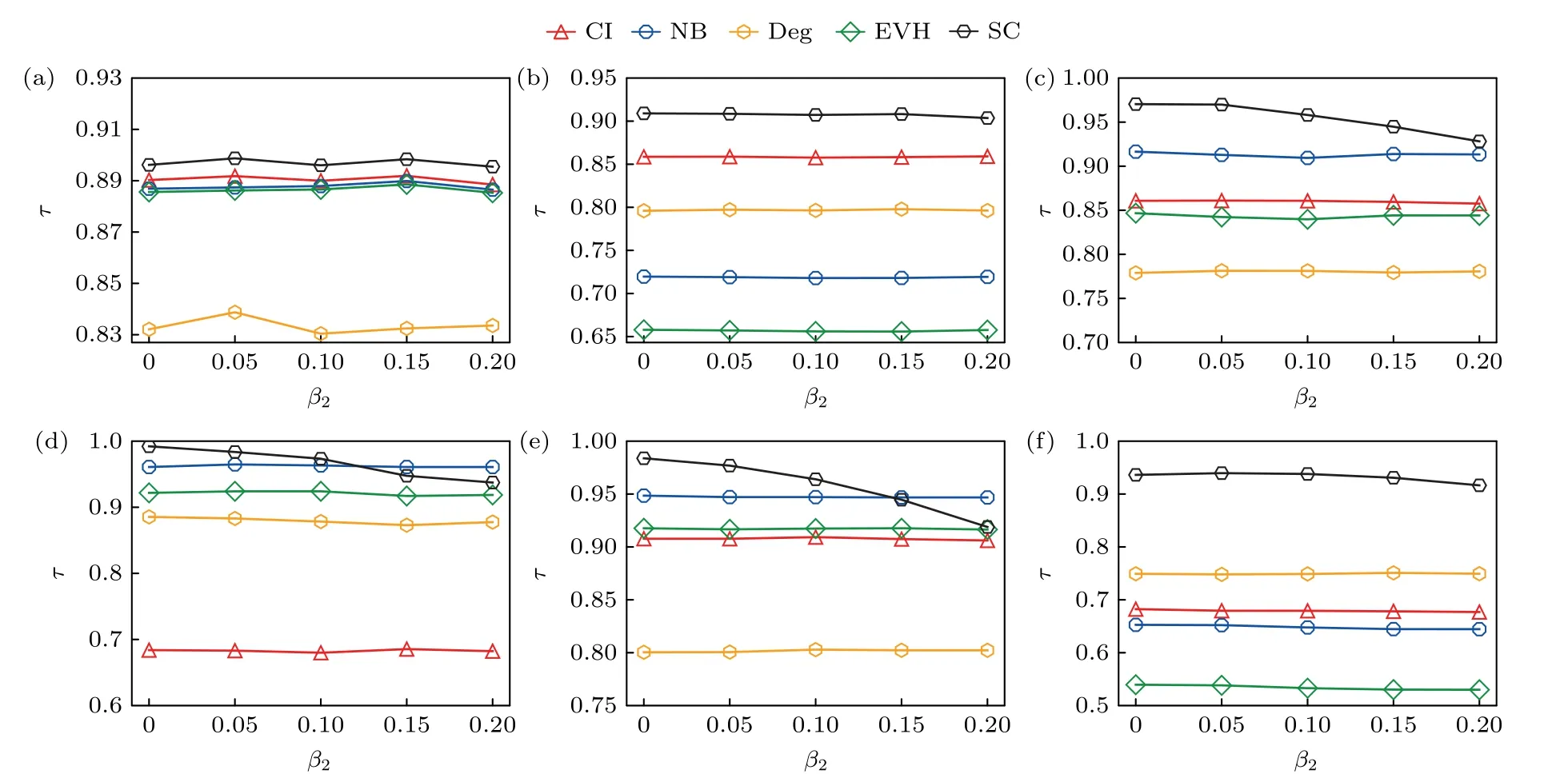
图5 不同2 阶单纯形传播速率 β2下,节点各中心性与传播影响力的肯德尔相关系数(a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13Fig.5.Kendall’s tau correlation of the centralities and the spreading influence of nodes under different 2-simplex spreading rates β2 : (a) RSC;(b) SFSC;(c) InVS15;(d) LH10;(e) SFHH;(f) Thiers13.
最后,通过Top-K准确率表征各中心性对前K个最有传播影响力节点的识别准确率.表2 展示了各中心性的Top-10,Top-20 与Top-30 准确率.综合来讲,传播中心性多数情况下能较为准确地识别前K个最有影响力的传播者.当K=10时,在RSC,InVS15,SFHH 与Thiers13 网络中,传播中心性有着最高的Top-10 准确率,即在识别前10 个影响力最大的节点时,传播中心性SC 准确率最高.当K=20时,在除SFSC 网络外的其他网络中,传播中心性有着最高的Top-20 识别准确率.当K=30时,传播中心性在SFSC,LH10 与Thiers13网络中有着最高的Top-30 识别准确率.Thiers13网络中,传播中心性有着最高的Top-K准确率,且明显高于所有基准中心性的Top-K准确率.传播参数设置如下:β1=,β2=0.1,µ=1 .
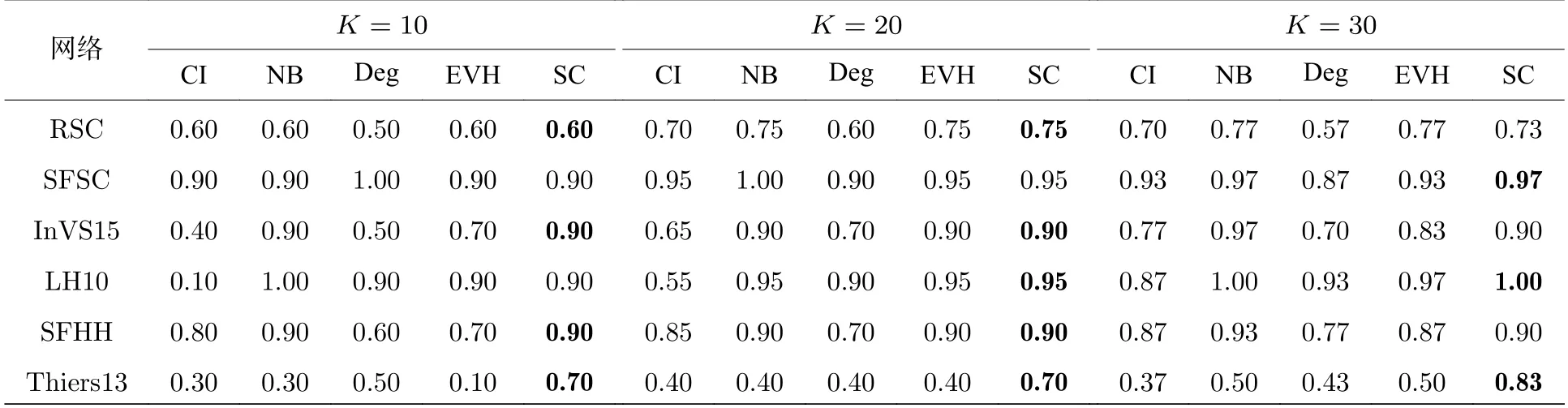
表2 各中心性的Top-K 准确率Table 2.Top-K accuracy of centralities.
6 结论
识别网络传播中最有影响力的传播者是控制传播过程的关键步骤之一.本文研究高阶网络上SIR 传播过程中最有影响力传播者的识别方法.我们提出单纯复形上SIR 微观马尔可夫链方程组,用于描述SIR 传播动力学过程.利用微观马尔可夫链方程组,计算单源传播时各节点被感染的概率,定义度量节点传播影响力的指标,传播中心性.大量仿真实验表明,传播中心性与节点真实传播影响力高度正相关.相比于4 种基准中心性,即高阶网络上的度中心性、特征向量中心性等仅考虑网络结构的中心性与复杂网络上最优的集体影响中心性、非回溯中心性,本文提出的传播中心性在两类合成网络中识别传播重要节点时比基准中心性更准确,在真实网络中多数情况下优于基准中心性.传播中心性方法可以扩展到超图上.对于超图上的传播,可以类似地写出描述传播动力学的微观马尔可夫链方程组,再利用该方程组计算节点的传播中心性.
传播中心性具有一定局限性.通过节点被感染概率预测节点的真实传播影响力时,假设越容易被感染的个体越容易感染邻居,即感染与被感染是对称的.考虑感染与被感染的方向性,当传播发生在1 阶单纯形上时,感染与被感染是对称的;当传播发生在2 阶单纯形上时,2 阶单纯形中单个感染态节点并不能通过该2 阶单纯形传播流行病,感染与被感染是非对称的.感染与被感染的非对称性会降低传播中心性的排序准确性,考虑2 阶单纯形上的非对称性可以进一步提升传播中心性的准确性.当感染与被感染的对称性受到严重破坏时,传播中心性可能不再适用.例如传播在有向网络上发生时,传播中心性可能不再准确.因此,未来需要进一步探索如何在有向网络上识别最有影响力的传播者.

