复原胞超光栅中负透射的鲁棒性

郭海琴,杜骏杰

（华东师范大学 物理与电子科学学院,上海 200241）

0 引言

光电混合集成芯片和全光芯片技术是下一代信息技术产业发展的潜在突破方向之一,它们有希望解决目前微电子芯片由于最小线宽越来越接近物理极限所带来的技术“瓶颈”.不仅如此,为了生产、生活的便利化,常用的普通光学元器件也有微型化的需求.人工光学材料是以纳米粒子为基本单元构造的新型材料,由此设计的几微米或几十微米的光学单元即可实现对电磁波的调控,是解决光学元器件集成化和微型化问题的有效方案.早期的人工光学材料包括光子晶体[1-2]和超材料[3-5].光子晶体的主要物理思想源于自然晶体中的电子能带结构理论[6],它的目的是获得属于光子的能隙或丰富的色散关系.超材料的物理基础是等效媒质理论,以亚波长谐振单元为人造“原子”定义出任意数值的等效介电常数和磁导率.目前,超材料实现了如负折射[7-9]、超棱镜[10]、电磁隐身[11-13]、光学黑洞[14]等传统材料无法取得的现象.然而,光子晶体和超材料都属于体材料,这类材料的尺度通常至少是波长量级或是波长的几十倍,无法做到更小.更严重的问题是,构成体材料的三维纳米粒子阵列的精细加工超过了目前的技术极限,使得体材料的批量生产难度很大.因此,很多与它们相关的研究成果仅限于实验室展示,无法真正走向应用.

与体材料难以加工不同,以超表面和超光栅为基础的平面光学通过纳米粒子的单层阵列来操控光波,加工实现的难度大大降低,成为近年来人工光学材料的研究热点之一.除了易于加工,平面光学材料相比体材料还具有更高集成度、更微型化、更低吸收损耗等优势.超表面[15-16]为光学诸多方面的突破和发展提供了可能,但通常超表面对光波的操控效率比较低,并且超表面的一个周期单元要由一系列不同的纳米粒子来构成.就目前的纳米分辨极限而言,批量加工仍是巨大的挑战.而构成超光栅的所有纳米粒子都是相同的,粒子的几何形状或尺寸不需要像超表面那样梯度变化,加工难度进一步降低.超光栅的调控对象是光栅所支持的各个衍射级,超光栅通过抑制低阶衍射级而使出射光完全沿着某一高阶衍射级方向传播,其理论操控效率通常可达100%.根据经典的光栅理论,光栅的高阶衍射级对入射角和波长的微小变化非常敏感,因此实现了高阶衍射的超光栅不仅可以控制光束的传播方向,也可以用于发展超光栅全息技术[17-18]和设计柔性变色板[19].

超光栅[20-29]里最引人注意的是介质超光栅,其吸收损耗几乎可以忽略不记,许多情况下又与互补金属氧化物半导体(complementary metal oxide semiconductor,CMOS) 工艺兼容,在应用上具有独特优势.对介质超光栅的研究已取得了很大进展,最早发现的超光栅也是介质超光栅,其中发生的负向透射现象可在单原胞和复原胞这两种结构中实现,复原胞结构的效率更高,可达93%左右[20].后来的研究调整了复原胞结构中大/小柱子的位置,获得了完美效率的负向透射现象[30].本文将进一步详细调查实现完美效率超光栅的各种可能的复原胞组合,并研究各种组合下,复原胞内小柱子半径与位置的变化对负向透射效率的影响.实际加工中,柱子半径与柱子位置都存在一定的误差,研究这些不确定性对高效超光栅的制备具有很大的指导意义.

1 结构模型与理论计算

本文研究的复原胞是由2 个半径不同的纳米柱(大/小纳米柱)组成.图1(a)给出了复原胞超光栅的截面示意图: 大/小纳米柱的半径分别为R和r,复原胞沿y方向以d为周期排列成一条直线.对于固定频率的入射波,晶格常数d保持不变,但复原胞结构内小柱子的方位以及与大柱子间的距离都可变.图1(a)仅显示了小柱子中心正好处在光栅轴线上的情形.本文研究的高斯光束(Gaussian beam)磁场沿z方向振动(transverse-electric,TE 极化波),入射角为θi,入射波波长为λ,入射波矢量大小记为ki=2π/λ.

图1 (a)复原胞超光栅的结构示意图;(b)入射角 θi=45°,晶格常数 d=时,超光栅支持的4 个衍射级Fig.1 (a) Schematic diagrams of metagratings with a complex unit cell;(b) The four diffraction orders are supported by a metagrating of d= at an angle of incidence,θi=45°

超光栅所处的背景介质的介电常数和磁导率分别为ε0和µ0,构成超光栅的柱子的介电常数为ε,磁导率为µ.这里考虑所有媒质都是非磁性的,即µ0=µ=1 .由光栅方程,入射角θi和晶格常数d决定了光栅能够支持的所有衍射级,即光束所有可能的出射方向.光场在这些出射方向的能量分布与纳米柱的半径R、r和介电常数ε等都有关系.本文以单原胞超光栅为例,首先介绍在各衍射级方向上透射率和反射率的计算方法,因为复原胞超光栅的透射率和反射率只要在此基础上稍作推广即可得到.

首先介绍单个柱子的米氏散射系数αn.这里入射场(Hinc) 和散射场(Hs) 分别展开为

式(1)—(2)中: Jn和分别为第n阶贝塞尔(Bessel)函数和第n阶第一类汉克尔(Hankel)函数;求和中的第n项表示第n个角动量通道.根据散射场和内部场的连续性条件可以求出米氏散射系数

超光栅是由柱子组成的一个一维周期性阵列,标记为0 的柱子(其坐标(0,0)) 的散射场系数可以在晶格求和的基础上得到.根据Floquet 定理,其他任意柱子,如第l个柱子(坐标(0,Rl=ld))的散射系数满足

这里,βν为第ν阶衍射级波矢量的x方向分量,可以表示为

式(6)—(9)中:kν为第ν阶衍射阶级波矢量的y方向分量,且kν=ky+gν,其中,ky=kisinθi,gν=2νπ/d(ν=0,±1,±2,···) 为周期结构的倒易晶格矢量,ν为阶数,亦即说明光的衍射方向时的级数;rν、tν分别是反射系数和透射系数,它们的表达式分别为

则反射率(Rν) 和透射率(Tν) 分别为

2 结果与讨论

本文分两种情况分别分析了复原胞内部结构对超光栅的影响: 第一种,分析了复原胞中大/小柱子相对位置改变对负透射率的影响,寻找不同相对位置下可以导致高负透射率的大/小柱子半径;第二种,固定复原胞内大/小柱子的半径,分析了小柱子与大柱子相对位置的改变对负透射率的影响.

2.1 不同的大/小柱之间的距离下,半径改变对负透射率的影响

对于入射角45°,波长1 550 nm 的光,为了使硅柱子构成的超光栅仅支持第0 级衍射和第-1 级衍射,光栅的晶格常数取为d=1 096 nm.对小柱子恰好处在两个相邻大柱子中间的情形,已有文献给出了近完美负透射率下复原胞两个柱子的半径大小[30].这里本文将小柱子沿y轴负向移动一个距离,使小柱子向大柱子靠近,研究大/小柱子间相对位置变化对负透射率的影响,调查能否仍然得到完美负透射率.图2(a)中左右两图分别显示了小柱子移动前后,复原胞及超光栅的结构变化,其中,δd=0 表示较小的柱子位于两个相邻较大柱子中心连线的中点;图2(b)分别显示了4 个不同的移动距离δd下,负透射率和复原胞内大/小柱子半径的关系,其中的红色区域表明4 个δd下都可以实现完美负透射,且每种情况下都有很多实现完美负透射率的复原胞组合.因此,相比于由单柱子组成的超光栅,无论复原胞内大/小柱子之间的位置怎样,复原胞超光栅在实现完美负透射方面都有很大优势.

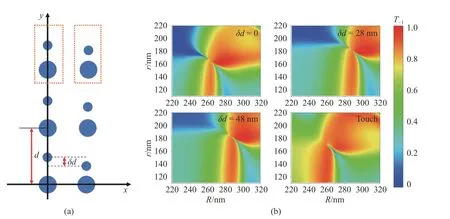
图2 (a)小柱子的位置移动 δ d 后复原胞的结构的变化示意图;(b) θi=45°,d=1 096 nm ,λ=1 550 nm 时,不同δd下R、r 与第–1 级透射率的关系图Fig.2 (a) A schematic diagram illustrating a variation of complex unit cell configurations,achieved by moving the position of the small rod by a distance δ d ;(b) A heatmap illustrating the transmissivity of the negative first order transmitted wave,T–1,with varying radii of the small rod and large rod(r and R,respectively) for different complex unit cell configurations,the fixed δ d value is different in each heatmap,with θi=45°,d=1 096 nm,and λ=1 550 nm

2.2 大/小柱半径固定不变,距离改变对负透射率的影响

下面固定复原胞内大/小柱子的半径,研究大/小柱子相对位置的变化对负透射率的影响.这里考虑“非粘连”和“粘连”两种复原胞结构.

2.2.1 “非粘连“复原胞内大/小柱子间距对负透射率的影响

将复原胞内大/小柱子不互相接触的结构称为“非粘连”结构,图2(a)所示的就是两种“非粘连”结构.现在固定“非粘连”结构中大/小柱子的半径,研究小柱子的位置偏差对负透射率的影响.本文的计算表明,在不同的大/小柱半径组合时,小柱子的位置对负透射率的影响不同.当复原胞内大/小柱子半径分别为R=274 nm,r=161 nm,而其他参数与前文所述相同时,小柱子位置在较大范围内变化,超光栅的负透射率都可以保持百分之百.因此R=274 nm,r=161 nm 是本文能够找到的最优组合.图3(a)显示了该组合下小柱子移动的距离δd和超光栅负透射率的关系图.可以看出,在20 nm 长的移动范围内,超光栅都可以实现完美负透射,20 nm 以内的位置偏差在实际加工中是完全可控的.随着小柱子移动距离的进一步增大,阵列的负透射率在缓慢下降,但即使δd达到110 nm,阵列的负透射率仍能保持90%以上.图3(b)和 图3(c)所示是δd=20 nm、δd=106 nm 时对应的磁场分布.从图3(c)中可以看出,当δd=106 nm 时,第-1 级反射方向出现明显的干涉现象,所以有部分光沿着第-1 级反射方向传输.按照上述求解单层柱状纳米棒阵列的散射率的公式,计算得出这种情况下第-1 级反射率为8.4%,第-1 级透射率为91.3%;而当δd=20 nm 时,如图3(b)所示,计算得出有98.79%的光都沿着第–1 级透射方向传播,几乎没有能量损耗.

图3 (a)随着小柱子位置 δ d 的改变,负透射率的变化曲线;(b)、(c)为高斯光束入射到复原胞超光栅中的磁场分布,其中,(b) δ d=20 nm,(c) δ d=106 nm.Fig.3 (a) The transmissivity of the negative first order transmitted wave,T–1,as a function of the change in position of the small rod in the complex unit cell,δ d ;(b),(c) The distribution of magnetic field intensity is illustrated for a Gaussian beam striking a metagrating with a complex unit cell with(b) δ d=20 nm,and(c) δ d=106 nm

2.2.2 “粘连”型复原胞内小柱子所处的方位角对负透射率的影响

将大/小柱子互相接触的结构称为“粘连”结构.之前的研究中,小柱子的中心都处在大柱子阵列的轴线上.下面考虑“粘连”时小柱子方位角的变化对负透射率的影响.图4 中的插图展示了大/小柱子半径分别为R=260 nm,r=120 nm 时“粘连”型复原胞的4 种结构;入射频率(f) 与这4 种粘连型超光栅的负透射率之间的关系也在此图中给出.图4 中绿色线和红色线完全重合,表明小柱子处于大柱子正左方和正右方时,超光栅对光有完全相同的调控.当入射光的波长为1 560 nm 时,无论小柱子粘连于大柱子上边还是左边、右边,3 种复原胞结构的负透射率都达到最大,且最大值相同都是约93%.但对于小柱子粘连于大柱子下边的复原胞结构,超光栅对光的调控行为与其他3 种结构非常不同,第-1 级透射率在各频率下都很低,最高也仅达70%左右,所以这种结构在实际加工中不是建议的选项.另外,如果同时考虑工作频带的宽度,小柱子粘连在大柱子正上方在实现宽频带方面更具优势,

图4 由半径为R=260 nm,r=120 nm 的大/小柱子组成的4 种不同的“粘连”型复原胞超光栅的负透射率Fig.4 The relationship between transmissivity of the negative first order transmitted wave,T–1,of the metagratings and frequency.The relationship is investigated for four metagratings,each with different complex unit cells consisting of two touching rods of radii R=260 nm and r=120 nm

如图4 黑线所示,在入射光的波长为1 560 nm 附近黑色线在最宽频带下保持了较高的负透射率.

3 结论

本文主要探究了复原胞超光栅的几何结构对负透射率的影响.基于多重散射理论,给出了复原胞中小柱子处在不同位置下,能够实现完美负透射率的大/小柱子半径的参数范围,证明了负透射现象具有很好的鲁棒性.在详细的模拟和计算基础上,本文也得到了一个大/小柱子半径的最优组合,在此组合下小柱子位置在较大范围内变化,超光栅都可以保持完美负透射率,并给出了小柱子位置变化浮动范围.不仅如此,小柱子在大柱子正上方的“粘连”型超光栅可以实现较宽频带的高负透射率.本文的计算结果说明复原胞超光栅在实现完美负透射率方面更有优势,对复原胞超光栅在实现完美负透射率方面鲁棒性的研究和给出的最优选择方案为高效超光栅的批量制备提供了参考.