挠率对自旋粒子的作用

惠 鹏 ,薛 迅

（1.新疆大学 物理科学与技术学院,乌鲁木齐 830046;2.新疆大学 理论物理中心,乌鲁木齐 830046;3.华东师范大学 物理与电子科学学院,上海 200241;4.华东师范大学重庆研究院,重庆 401120）

0 引言

有挠的引力理论自广义相对论诞生后就从没停止过探索.在引力的Platini 形式中,宏观物质源产生的引力场是无挠的.用广义相对论描述,挠率仅可能存在于旋量物质源处,挠率没有动力学,不能传播,离开旋量物质源,挠率为0.很多修改的引力理论模型将联络也作为动力学自由度来考虑,赋予其联络动力学.这种动力学一般认为来自高能引力理论,如有研究将联络场类比量子色动力学的胶子场[1-3],在低能时会囚禁或者凝聚到Levi-Civita 联络上;高能时的联络场具有动力学激发,偏离Levi-Civita 联络,具有非平庸的contortion(扭率) 和挠率分布.量子引力理论一般都明显假设或者隐含了一个不变的普朗克(Planck)能标(EP),在接近该能标时理论具有尺度不变性,由此导致洛伦兹(Lorentz)破缺[4-6].量子引力的Lorentz 破缺效应经过暴涨会被冻结在超视界的大尺度上,导致在宇宙学尺度存在冻结的大尺度Lorentz 破缺效应.相应的大尺度Lorentz 破缺宇宙学模型预言了宇宙学尺度上非平庸的挠率和扭率分布作为暗能量的候选者[7-15].测量挠率对尺度的依赖关系可以确定在多大尺度上时空对称性开始偏离Lorentz 对称性,同时也可以为一些量子引力理论提供证据.

自旋自由度作为一种粒子的Lorentz 变换量子性质在广义相对论诞生之初并没有被发现和考虑过,但是采用局域坐标的标架场语言描述可以很自然地将自旋纳入广义相对论框架中,在局域标架的Lorentz 不变规范理论框架中,可以一般地给出挠率与物质场的作用形式.以Dirac 费米子为例,在平直时空中,Dirac 费米子满足Dirac 方程;在弯曲时空中,通过引进Lorentz 规范场,也就是Lorentz 联络来保持局域Lorentz 变换不变性,将平直时空Dirac 作用量中的普通导数替换为Fock-Ivanenko 协变导数,即得到弯曲时空中局域Lorentz 不变的Dirac 作用量,相应地可得到弯曲时空中最小耦合的Dirac 方程.挠率张量本身在Lorentz 变换下可以分为3 个不可约部分: 矢量、轴矢量和纯张量.在最小耦合的Dirac 方程中,可以证明挠率的矢量部分和纯张量部分的贡献为0,只有轴矢量部分起作用.考虑到与挠率耦合的物质场的重整化效应,重整化抵消项会产生有效的挠率非最小耦合项,即使挠率与旋量物质场的裸耦合只有轴矢量与旋量场耦合,重整化抵消项也会诱导挠率与旋量场的非最小耦合.非最小耦合项是普适的,在非最小耦合情形,矢量挠率和轴矢量挠率都会与旋量场耦合[16-17].

挠率与旋量场的耦合导致挠率对自旋的作用,在经典极限下,这种作用体现为挠率–自旋作用力.从带挠率耦合的Dirac 方程得到挠率对自旋粒子的作用力,以及自旋在挠率作用下的演化问题,早在20 多年前Shapiro[16]就研究过,即可以通过对Dirac 方程的海森堡(Heisenberg)形式取经典极限来得到经典正则运动方程.这种得到经典自旋–挠率作用力的方法的缺点是,自旋算符没有经典对应,取经典极限时,自旋算符的意义不明确.有研究通过将带挠率耦合的量子力学问题拓展为超对称量子力学问题,再得到旋量粒子的经典运动方程.该方案的缺点是在模型的超对称扩展中,需要引入超对称坐标,但其在自旋粒子的经典运动方程问题中没有明确的物理意义.近年来,Trukhanova 等[18-20]利用几何–流体动力学框架研究了具有闵氏度规黎曼(Riemann)平直的黎曼-嘉当(Riemann-Cartan)时空中挠率对自旋和自旋粒子的作用,将挠率对自旋的作用处理为挠率对自旋算符的自旋波函数平均值,这样一个经典极限下有明确物理意义的三维矢量的作用,并将这种处理应用到了自旋粒子构成的多粒子体系[21].在宇宙学Robertson-Walker 度规背景下,时空不是Riemann 平直的,对于基于有挠引力模型的宇宙学模型,有给定挠率的时空背景,现有的几何–流体动力学方案对挠率的处理并不适用于非Riemann 平直[18-19].本文工作致力于将几何–流体动力学方案对挠率–自旋作用,从Riemann 平直闵氏度规背景推广到研究宇宙学的非Riemann 平直给定挠率的时空背景中挠率对自旋1/2 粒子的作用;从非最小耦合Dirac 作用量出发得出描述自旋状态变化的旋量方程;经过非相对论近似得出类Pauli 方程;用几何–流体动力学方法将自旋平均值对应到经典矢量,进而得出非相对论近似下的流守恒方程、动力学方程和自旋演化方程的一般形式,并将动力学方程视为自旋粒子的单粒子自旋平均后的半经典运动方程;最终考虑满足宇宙学挠率的情况,给出粒子速度和自旋平均值等物理量的具体解的形式.

1 弯曲时空的Dirac 方程

1.1 基本符号说明

本文采用希腊字母µ,ν,ρ,···表示时空指标,每个时空指标取 0,1,2,3 分别表示四维时空的四个维度;上下标用度规gµν,gµν升降;用拉丁字母i,j,k表示时空的三维空间指标,取 1,2,3 分别表示空间的三个维度;用拉丁字母a,b,c,d,e表示切空间指标,取 0,1,2,3 表示切空间时空的四维指标;闵氏时空度规ηab,ηab对角元取(-1,1,1,1) 升降;用拉丁字母l,m,n,o,p表示切空间的三维空间指标 1,2,3 ;时空指标和切空间指标用四标架联系,其与度规满足关系式

Dirac 矩阵采取的形式为

式(2)中:I是二阶单位矩阵;σi是泡利(Pauli)矩阵,为

克罗内克(Kronecker) δ 符号 为

Levi-Civita 符号采用定义

其中xµ是四维时空坐标.

本文采取自然单位制,普朗克常量(ℏ) 和光速(c) 都取1,即 ℏ=1 ,c=1 .

1.2 非最小耦合Dirac 作用量

弯曲时空中非最小耦合挠率的作用量参考[16]

η1,η2分别是矢量挠率和轴矢挠率的耦合系数,区别于[19]用最小耦合作用量来考虑自旋挠率作用,非最小耦合同时考虑挠率的矢量和轴矢部分,但纯张量挠率对Dirac 作用量没有动力学项,最小耦合对应的耦合系数为η1=0 和η2=1 .

1.3 Dirac 方程

由非最小耦合作用量式(7)出发得到Dirac 方程

选取满足宇宙学原理的Robertson-Walker 度规(R-W 度规)

其中a(t) 是宇宙演化的尺度因子.本文详细讨论的是空间平直k=0 的情况.

把Levi-Civita 联络在代数上也做类似式(8)和式(9)的分解,可以将Dirac 方程化为

为了讨论方便,下面不做说明使用新的定义符号,具体为

弯曲时空的Dirac 方程有四维流守恒方程

在有挠情况下,只要把自旋联络换成相应的有挠联络,就可以得到式(11)的流守恒方程

2 描述自旋1/2 粒子的半经典方程

2.1 Pauli 方程

Dirac 方程经过非相对论近似后可以得到Pauli 方程,以便进一步求出粒子的经典物理量的演化.先将四分量旋量波函数分为上下两个部分

将此结果带入式(13)可以得到2 个方程,具体是

对式(20)中第二式进行非相对论近似,保留零阶可得下分量χ,具体为

质量较大时,下分量远小于上分量.将此下分量带回式(20)中第一式,可得上分量φ的类Pauli 方程

Shapiro[16]直接从Pauli 方程出发得到算符演化Heisenberg 方程,并做经典极限 ℏ→0 得到经典运动方程.但自旋无经典对应量,所以要先解决自旋经典对应问题.Trukhanova[19]用几何–流体动力学方法对自旋先求平均,对应到一个经典三维矢量,这样就避开了这个难题.结合经典极限对应以及几何–流体动力学方法,本文从式(22)得到的非最小耦合挠率的Pauli 方程出发,先通过几何–流体动力学方法将自旋求平均,对应到一个经典矢量,然后求出经典运动方程.

2.2 自旋经典对应

先将二分量波函数进行分解,得到

式(24)中:A和B是四维时空坐标的实函数;φ是单位自旋波函数,可用两个实函数β和χ来表示,具体为

此旋量作为自旋态的一个基;再定义φr为

即可到一组描述自旋状态的正交归一的基,具体为

对Pauli 矩阵求自旋平均可得

这是三维空间的单位矢量,其物理意义是自旋角动量平均值在空间的方向.可以定义自旋本征态对应的自旋方向算符为.不难得出,此算符对应的本征态就是式(25)和式(26)中定义的2 个自旋态基底,其本征值分别为1 和-1,本征方程为

利用自旋态2 个基底,可以构造2 个态

利用它们对Pauli 矩阵平均,可以得到另外2 个单位矢量.若取自旋方向为z方向,则它们分别指向“x”方向和“y”方向(与自旋方向垂直且互相垂直的方向),即

它们与自旋方向构成正交归一的一组矢量,即

后面就以自旋方向nm为粒子自旋性质的经典对应来研究粒子自旋与挠率的作用,对其他物理量的影响也可以利用这种经典描述合理地给出经典结果.

2.3 流守恒方程与速度

通过Pauli 方程可以得到描述粒子经典物理量演化的方程.首先利用式(24)的分解方法代入式(22),然后求自旋平均,即左乘φ†,得到复方程

定义aµ是坐标表象下动量算符pi=i∂i与能量算符 i∂t对自旋求平均的部分,即

从式(18)直接做非相对论近似,式(21)得到的密度和三维流形式为

所以,由协变的流守恒方程直接非相对论近似得到的流与先做非相对论近似得到Pauli 方程求得的流一致.

通过流可以定义速度为

利用式(40)可得到三维流守恒方程

2.4 动力学方程

利用式(33)定义的速度,将式(33)的实部方程化简可得

式(47) -(49) 中:Υ项与自旋在空间中演化相关;M项为量子势[23].为得到动力学方程,将式(47)中的B消去,以速度为基本变量可以得到描述粒子速度演化的动力学方程

式(53)这两项类似于Lorentz 力的作用,是挠率自旋耦合的作用.

通过对式(22)左乘φr†,可得到自旋演化方程

其中,Ωq类似于磁场作用,即

广义相对论的测地线方程为[24]

在无自转自由降落系中,可以得到测地线方程三维形式

对比式(50)可以发现,在挠率和自旋的作用下,粒子的运动是会偏离测地线的;除此之外,在无挠情况下,还会有量子势的作用.此项可以看作量子涨落造成的影响,在大尺度下可以找到此项为0 的解[23].无挠情况下,若取ρ为常数作为经典极限,剩下的项化简可以写为

在无挠情况下,在无自转自由降落系对式(54)求解,可以得到自旋方向不变的解.式(50)中类洛伦兹力和Υ项在自旋不变时无作用,此条件下动力学方程与测地线方程一致.

通过式(46)、式(50)和式(54)组成的偏微分方程组以密度、速度和自旋方向作为变量,在给定挠率的条件下可以进行求解,得到这些物理量具体演化方式.

3 宇宙学背景下挠率对自旋1/2 粒子的作用

3.1 宇宙学挠率

满足宇宙学原理的挠率早有学者给出[25].结合本文使用的符号,挠率可以写为

此情况下只有时间分量有贡献,且它们都是时间的函数.

通过重新定义,可取挠率的2 个耦合系数都为1.将这些条件都代入式(46)、式(50)和式(54),取z轴为粒子传播方向,可以得到方程组

此结果使得式(62)和式(63)没有量子势贡献,只需求解这2 个准经典方程就可以得到粒子运动经典极限下的行为.

3.2 粒子传播路径与自旋演化

将式(62)和式(64)联立,取z轴为粒子发射源和接收点所在的轴线,先考虑不含尺度因子a和轴矢挠率A0的情况,可以得到解

式(65)—(66)中:v0是常数,轴矢挠率为0 时,粒子沿z轴运动,v0即为粒子沿z轴的运动速度;β是由初始自旋方向与z轴的夹角确定的常数.

粒子位移对时间一阶导数即为速度,即

通过对这些物理量取值,可以画出路径图以及自旋方向的变化图,详见图1.为展示路径与自旋细节,这里取质量(m)=1 kg ,速度(v0)=1 km/s,β=π/6 ,a=0.3 ,ξ=0.1 .由图1 可以看出,粒子在挠率作用下是沿螺旋线传播,自旋方向沿传播方向螺旋进动.

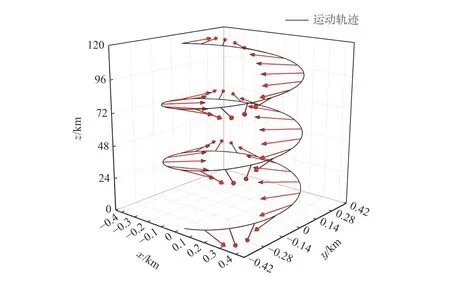
图1 粒子路径和自旋方向变化Fig.1 Particle motion path and change of spin direction

从含有轴矢挠率修正的Friedmann 方程

这里,a˙≡da/dt,¨a≡d2a/dt2.主要考虑暗能量

的影响.式(81)中,Ωλ=0.688 9 ,H0=2.2×10-18s-1.取粒子质量m=0.1 eV ,速度v0=0.1c,β=π/6,a=0.3 .

可以估测出ξ量级为 1 0-31,螺旋半径量级 1 0-5m ,螺旋周期量级为 1 029s(比宇宙年龄高十几个量级),所以此情况下挠率几乎没有影响.

从不含时的解出发,可以得到含时情况一阶近似解,为

式(82)—(85)中,v0和β是常数.式(83)后两项在β=π/2 的解中为0.与不含时情况相比,主要变化是螺旋进动的角速度和粒子传播速度会受自旋挠率耦合作用影响而随时间变化.从式(83)最后一项可以看出,挠率演化可以确定此项符号,粒子传播速度随挠率演化可能增加或降低.

式(83)对时间积分,并以式(70)做泰勒(Taylor)展开保留一阶项,可得粒子在传播过程中z轴的坐标变化,具体为

这种情况较为复杂,不能把粒子路径写成简单螺旋线的形式,在挠率随时间变化很小时,可以与不含时变化较为接近,路径总体接近螺旋线,自旋也做类似的进动变化.

4 结论

本文在前人研究挠率的基础上,选取合理的方法研究了挠率对自旋1/2 粒子的作用.首先,采取非最小耦合挠率,从而兼顾可能产生的重整化问题,合理地引入挠率.然后,由描述自旋状态的四旋量方程,通过非相对论近似得到二旋量的类泡利方程.由于目前无挠的广义相对论还是与观测吻合得很好,所以挠率作用较小,对于它采取非相对论近似而忽略高阶项的影响也是合理的.在得到经典方程之前,可以通过几何–流体动力学的方法对无经典对应的自旋进行处理,以自旋平均后的自旋方向(式(28))为描述自旋变化的经典量.最后,得到在宇宙学时空任意挠率背景下,以粒子密度、速度、自旋方向为变量的一组动力学演化方程(式(46),式(50),式(54)).

与广义相对论自由降落无自转系测地线方程对比,挠率会有类似Lorentz 力的作用,使粒子的运动偏离测地线,在常数挠率作用下,粒子可能会沿测地线螺旋进动.而对自旋演化,广义相对论没有相应的描述,从结果上看,自旋方向受挠率的影响发生变化,且自旋的变化也会影响到粒子动力学.在挠率为0 时,自旋粒子沿测地线运动.

由于挠率对自旋粒子的作用可能在大尺度下才能观测到与广义相对论的明显差别,并且一些量子引力理论最终也会导致大尺度下有挠率.基于这两点,针对宇宙学时空背景下进行具体求解.得到宇宙学矢量挠率只影响粒子密度,可以视为粒子的有效质量受其影响发生了变化.粒子运动轨迹为螺旋线,其自旋方向沿传播方向进动.粒子的传播速度会随着挠率的演化而增加或减小.