中心力场中的电子涡旋

周永香 ,薛 迅,2,3

（1.华东师范大学 物理与电子科学学院,上海 200241;2.新疆大学 理论物理中心,乌鲁木齐 830046;3.华东师范大学重庆研究院,重庆 401120）

0 引言

涡旋现象普遍出现于很多系统中,比如在经典流体系统[1-2]、量子流体系统[3-5]、非线性场系统[6]和光学系统[7]中.携带轨道量子数l的光波构成光学中的涡旋现象[8-9].文献[10]首次将涡旋光波的概念推广到了电子涡旋波,即携带轨道角动量的传播电子态.涡旋波的普遍特征是其等相面为连续螺旋面.在以传播方向为轴向的柱坐标系中,其波函数具有轨道角动量本征态 eilφ形式的相位因子,其中,φ是关于传播轴的方位角,l为轨道角动量量子数.涡旋波波函数具有连续螺旋状的等相位面[11-15],量子化的涡旋可以对应到带非平庸拓扑数的拓扑孤立子解.Nye 等[16]首先观察到这种非平庸的拓扑结构,他们认为这是波列中类似于晶体缺陷的螺旋式位错.

对电子涡旋态的描述可以借助薛定谔(Schrödinger)方程、狄拉克(Dirac)方程、克莱因-戈登(Klein-Gordon)方程的涡旋波解.这3 种方程的涡旋波解分别描述了电子涡旋波的非相对论极限、电子涡旋波的相对论旋量结构和电子涡旋波的相对论行为[10,17-22].由于电子涡旋波携带轨道角动量,其波函数表现为具有角动量本征态 eilφ形式的分离变量解,等相面为螺旋面.在非相对论Schrödinger 方程研究框架中,自由电子和恒定磁场中的电子具有守恒的轨道角动量分量,均保证了在波函数中存在角动量本征态 eilφ形式的分离变量解[23].涡旋波形式的波函数解可以是电子的可能运动状态.对自由电子,从Dirac 哈密顿量(H)来看,总角动量是守恒的,但轨道角动量和自旋角动量的z分量各自并不守恒,而在非相对论极限下,自由电子的哈密顿量与轨道角动量的z对易.为了将相对论协变的理论过渡到非相对论极限,Barnett[24]指出,正确的做法是借助Foldy-Wouthuysen(F-W)变换,这样才能得到正确的Schrödinger 方程,并作为相对论电子波动方程的非相对论极限,使哈密顿量、电子波函数与轨道角动量具有良好的定义.F-W 变换对Dirac 旋量做幺正变换,使得Dirac 哈密顿量对角化,即取表象使上下旋量满足的方程可以分离,在该表象下轨道角动量和自旋角动量分别守恒.同时Barnett[24]还指出,在相对论Dirac 方程下的轨道角动量(L)和自旋角动量(S)此时应该有新的定义—L＇和S＇,这个L＇和S＇与相对论情况下的Dirac 哈密顿量对易,从而说明携带轨道角动量的自由电子在相对论系统中仍然有好的轨道角动量的定义.同样在相对论协变下,恒定磁场中的携带轨道角动量的电子也具有不守恒的轨道角动量和自旋角动量,但是在非相对极限下,恒定磁场中的电子所对应的哈密顿量与轨道角动量L对易.2020 年,Zou[25]等同样利用F-W 变换,将此时电子所对应的Dirac 哈密顿量变为对角化的哈密顿量,从而分离上下旋量方程,得到相对论情况下对应的涡旋解,以及在均匀磁场中电子沿z轴传播对应的涡旋解的古伊相位(Guoy phase).Barnett[24]和 Zou 等[25]虽然选取了轨道角动量不守恒的相对论系统,但通过前面的介绍可知,即使在相对论情况下的Diarc 哈密顿量与轨道角动量不守恒,仍然可以利用表象变换找到与轨道角动量对易的哈密顿量;而且这个幺正变换也可以重新定义“新的轨道角动量”,使在相对论系统中同样存在守恒的轨道角动量,保证在新的表象下(Foldy-Wouthuysen(F-W) 表象) 的波函数中,存在轨道角动量的本征态 eilφ的分离变量解,从而证明自由电子和恒定磁场下相对论电子涡旋的存在.

在前面所介绍的相对论系统中,可以通过F-W 变换证明此时的相对论系统仍然存在守恒的轨道角动量.在自然界中存在大量的系统均不存在守恒的轨道角动量,如中心力场中运动的电子,在相对论情形下类似自由电子,具有不守恒的轨道角动量和自旋角动量.经过F-W 变换后,又因为此时的势能项与坐标有关,所以在F-W 变换之后哈密顿量中存在自旋–轨道耦合项,导致此时幺正变换之后的哈密顿量同样与轨道角动量不对易.那在这种系统中还能得到电子涡旋解吗？本文就是基于这一目的,从中心力场中的Dirac 方程出发,经过F-W 表象变换,找到在中心力场中携带轨道角动量的电子沿z轴传播的涡旋解,以及此时所对应的等相位螺旋面.

1 中心力场中的电子涡旋

1.1 中心力场中的Dirac 方程

中心力场中的电子满足Dirac 方程

其中,σi(i=1,2,3) 为泡利(Pauli)矩阵,I为 2×2 单位矩阵.

从式(1)和式(2)中很容易看到,[Lz,H]≠0,[Sz,H]≠0,[Jz,H]=0 .所以此时无法判定,在相对论情况下,中心力场中携带轨道角动量的电子沿z轴传播时,是否存在 eilφ的分离变量解.为了简单起见,可以借用Barnett[24]所提出的F-W 表象变换,将相对论Diarc 方程和非相对论下的Schrödinger 方程联系在一起,构造一个对角化的哈密顿量,从而使四分量旋量中的上下分量分开: 一个二分量方程构成Pauli 方程;另一个二分量方程描述负能解.

1.2 F-W 变换

对式(2)的H做F-W 变换.类似于自由电子下的F-W 变换,先对H进行分类: 一类为与β反对易的奇算子,用θ表示,满足{θ,β}=0 ;另一类为与β对易的偶算子,用ε表示,满足 [ε,β]=0 .因此H的分类为

式(6)所表示的H＇＇满足做F-W 变换的目的:将哈密顿量变为只包含偶算符的对角化矩阵,从而能够使四分量波函数分离成2 个二分量旋量.所以经过F-W 变换之后的Schrödinger 方程为

可以看到,在式(10)中的哈密顿量因为存在自旋–轨道耦合项,并不与轨道角动量和自旋角动量对易,即 [Lz,H＇＇]≠0,[Sz,H＇＇]≠0,但满足 [Jz,H＇＇]=0.这正是与之前的研究中不同的地方.在之前的有关电子涡旋波的研究中,轨道角动量守恒是电子涡旋解存在的条件,如在非相对论系统中的自由电子和均匀磁场中的电子;而在相对论系统中,即使Dirac 哈密顿量与轨道角动量并不对易,但是经过FW 表象变换之后,便可以找到与轨道角动量对易的哈密顿量,而且在F-W 变换之后,也可以定义“新的轨道角动量”使得在相对论系统中仍存在守恒的轨道角动量,从而使在F-W 表象下电子的沿z轴传播解具有涡旋结构.但在本文的研究中,考虑的是在F-W 变换之后,哈密顿量与轨道角动量和自旋角动量仍不对易,但因为存在总角动量守恒,可以用轨道角动量对应的本征态 eilφ和自旋的±1/2 的纠缠态去描述此时的涡旋结构.所以对于式(10)中的与总角动量对易的哈密顿量,其对应的波函数可以用总角动量的z分量Jz的本征波函数去描述,即

式(14)和式(15)这2 个方程与傍轴方程具有相似性.傍轴方程为

是对自由电子在柱坐标中的Schrödinger 方程

运用了傍轴近似∂2/∂z2≈2ik(∂/∂z)+k2.因为式(16)中的哈密顿量与Lz对易,可分离 eilφ的变量解.令ψ=u(r,z)eikzeilφ,代入式(16),可得

令τ=ρ2,可得到满足广义拉盖尔(Laguerre)多项式的方程

对于式(16)所对应的解,便可得到

式(14)和式(15)与傍轴方程(式(16))具有相似性,故可以对式(14)、式(15)这2 个方程也利用傍轴近似∂2/∂z2≈2ik(∂/∂z)+k2[30-31],并令a=eikza＇,b=eikzb＇,则a＇,b＇是只与(r,z) 有关的函数,与φ无关.代入式(14)、式(15)分别可得

其中,l＇=l+1 .

对于方程(23)和方程(24)无法像解傍轴方程一样,引入无量纲量ρ(r,z) 将方程变为只含ρ的常微分方程.故引入表示微扰程度的参数γ.令a＇=φ0+γφ1,b＇=η0+γη1,代入式(23)、式(24),得到γ的零次幂所对应的2 个方程

即为式(22)去除 eikzeilφ的解.

对于γ一次幂的2 个方程,先看第一个方程(式(27)),此时可以视为对有源的场方程求解.对其两边同时乘以 eikzeilφ,并还原傍轴近似,便可得到

2 柱坐标下的Green 函数

将式(35)化为柱坐标下的Green 函数方程,可得

对于 δ(φ-φ＇),δ(z-z＇),可用φ,z方向的正交归一函数来表示,即

其中,gm(r,r＇) 为r方向的波函数.

将式(38)和式(39)代入式(37),可得

其中,K为径向波数的平方,即K2=k2-kz2.当r≠r＇时,式(40)对应着贝塞尔(Bessel)函数的2 个线性独立解: Jm(Kr) 和 Nm(Kr) ,其中,Jm(Kr) 为第一类Bessel 函数,Nm(Kr) 为第二类Bessel 函数.所以可设式(40)中的解: 当r＜r＇时,P1(Kr) 为第一类Bessel 函数和第二类Bessel 函数的某一线性组合,它满足适当边界条件;当r>r＇时,P2(Kr) 为另一线性组合,它满足固有边界条件,其表达式为

此时便可利用文献[34]所介绍的方法得到在柱坐标系下的Green 函数的解

对于式(43)和式(44),可以用 δ 函数进行进一步的化简.因为Laguerre-Gauss 傍轴解φ0,η0中均不含方位角φ,所以可得

3 结论

由a＇=φ0+λφ1,a=eikza＇,便可以得到对于旋量波函数u的上分量 eilφa.相应公式为

可以看出,上旋量中Lz的本征态 eilφ的存在.

对式(53)做数值积分并画图,可以得到,当ρ一定时,ψ所对应的螺旋线如图1 所示,其中,ρ=r/W(z) 为无量纲径向坐标参量,波形每旋转一周转动波函数 eilφ相位变化为 2π .当携带轨道角动量的电子在中心场中沿z轴运动时,旋量上分量解φ所对应的螺旋等相位面如图2 所示,其中,轨道量子数l=1 ,波形每旋转一周相位变换为 2 π .

图2 旋量上分量解 φ 所对应的螺旋等相位面Fig.2 The helical equiphase surface of the spinor upper component solutionφ

根据上面得到的旋量上分量的方法,同样可以得到中心力场下的电子沿z轴运动时的旋量下分量解

取径向量子数n=0 的束缚基态和l=1 ,式(54)给出了不同的旋量下,分量等相面和不同常ρ面的螺旋线交线,详见图3 和图4,以及中心力场中的携带轨道角动量的电子沿z轴传播时,其旋量下分量η的等相位面,详见图5,其中ρ=r/W(z) 为无量纲径向坐标参量.

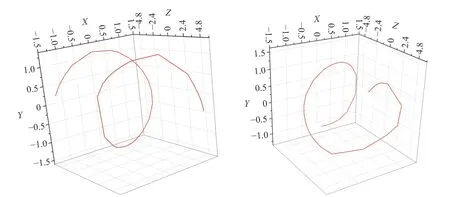
图3 z 取值从 - 6 到 6 时,旋量的下分量等相面与 ρ=1.2 面所交的涡旋线Fig.3 The spiral line intersected by the spinor lower equiphase and ρ=1.2 surfaces with the value of z ranging from - 6 to6

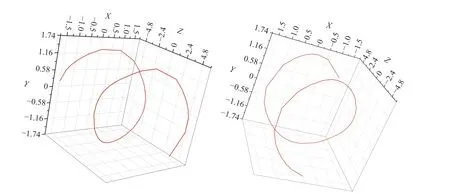
图4 z 取值从 - 6 到 6 时,旋量的下分量等相面与 ρ=1.5 面所交的涡旋线Fig.4 The spiral line intersected by the spinor lower equiphase and ρ=1.5 surfaces with the value of z ranging from - 6 to6

图5 旋量下分量 η 的涡旋解等相面Fig.5 The helical equiphase surface of the spinor lower component solutionη

由图3 和图4 可以看到,当轨道量子数l＇=2 时,旋量下分量等相面与等ρ面所交螺旋线为2 条.通过观察图5 则更清晰地看出,当选择同一相位时,此时对应的螺旋等相面却有两种不同的情况,这是因为初相位选择可以相差 π 的整数倍,而选择奇数倍和偶数倍就会导致相应的X,Y反号,因此导致了图3、图4、图5 中对于同一个等相位面,具有两种不同的情形.

本文所求得的二分量旋量作为Dirac 旋量在F-W 表象中式Dirac 旋量的上旋量,经F-W 逆变换会将上下旋量纠缠起来,下旋量由上旋量给出,其在中心力场中的自旋涡旋纠缠态解,会使Dirac 旋量整体具有涡旋结构.这样非相对论极限的涡旋解经过F-W 逆变换就可以给出相对论Dirac 旋量的涡旋解[25].

根据上面的数学表达式和图形展示,可以看到携带轨道角动量的电子在中心力场中沿z轴传播时,确实存在涡旋解及所对应的螺旋等相位面,这说明在中心力场中传播的电子确实具有电子涡旋结构.而且本文的研究是在轨道角动量不守恒的中心力场中,与之前的电子涡旋波的研究有很大的不同.之前的研究都是在可以得到守恒的轨道角动量的系统中,比如自由电子和均匀磁场中的电子,在这类系统中,能够分离轨道角动量的z分量的本征态 eilφ和自旋波函数的±1/2 解,从而得到人们熟知的涡旋解;而在中心力场下需考虑F-W 变换之后的自旋–轨道耦合效应,这就使得中心力场中电子所对应的哈密顿量并不与轨道角动量对易,但此时的体系总角动量守恒,可以构建电子自旋态与轨道涡旋态的纠缠态,这种涡旋波是二分量旋量涡旋波.

本文为轨道角动量不守恒的系统提供了新思路.因为总角动量守恒的限制条件比之前的条件限制更弱,所以能为更多的轨道角动量不守恒但总角动量守恒的系统证明该系统仍然具有涡旋结构.中心力场诱导自旋轨道耦合的体系对于电子的传播环境比自由电子和匀强磁场中运动的电子更具有普适性,其旋量涡旋波比单纯的轨道涡旋波有更高的稳定性和实验上的可实现性.另外,由于中心力场是大自然中较常见的势能场之一,而且中心力场在许多方面也有重要作用,比如中心力场在原子结构和原子核结构的研究中均占有重要地位,所以研究中心力场中的电子涡旋结构可以帮助人们更好地认识原子内部结构;中心力场与引力场的形式也很相似,因为在宇宙中存在大量携带轨道角动量的射线,但是在引力场的度规下,很难得到与轨道角动量对易的哈密顿量,而总角动量守恒的条件又相对较弱,所以便可以利用本文所描述的方法来更好地考虑引力场中的电子涡旋,从而为宇宙射线的观测开辟新的对象.