基于物理模型的BaZrO3钙钛矿机器学习力场

赵 亮, 牛宏伟, 荆宇航

（1.中国航发北京航空材料研究院，北京 100095；2.哈尔滨工业大学 航天学院，哈尔滨 150001）

高性能航空发动机往往要承受更高的涡轮进口温度。目前，推重比10一级的航空发动机涡轮前温度已经超过1800 K，推重比的提高将进一步提升涡轮前温度。镍基高温合金作为当前涡轮叶片的主要材料，其耐高温能力只有1373 K，因此为了保证长期可靠工作，涡轮叶片普遍由镍基单晶基体、热障涂层（TBC）以及复杂气冷结构组成。其中，热障涂层在提高涡轮前温度和延长叶片使用寿命方面成效显著，已成为高性能发动机研制的关键技术之一。20世纪，美、英、法、日、俄等国家都在积极研究热障涂层的设计与制备技术，并大量应用于航空发动机热端部件。进入21世纪，热障涂层技术逐渐成熟并得到广泛应用。俄罗斯的苏-30和苏-35战斗机的喷管都使用了热障涂层材料，而美国目前几乎所有的军用和民用航空发动机都采用了热障涂层技术[1-4]。

钙钛矿[5-8]结构化合物具有高熔点、低热导率以及高膨胀系数等特点，是热障涂层陶瓷的备选材料之一，典型的包括BaZrO3（BZO）等。很多学者对BZO进行了大量的密度泛函理论（DFT）计算研究，例如其结构、热力学和质子传输方面，特别是在掺杂状态下[9]，因为掺杂物会引起结构畸变并影响质子传输能力。BZO基态结构的中子散射实验和第一原理计算[10]揭示了不稳定的声子模式是一种过渡现象，这与ZrO6八面体的旋转有关，这些依赖于交换相关函数的计算表明了BZO的结构是稳定立方钙钛矿氧化物。BZO作为一种脆性材料，它的力学行为受到其自身固有微观结构的强烈影响[11-12]，如晶界、预先存在的微裂纹、晶粒和孔隙。这些微结构的取向、尺寸、形状和空间分布控制着材料的开裂、延伸、相互作用和最终失效[13-14]。因此，这些微观结构的变化可以改变裂纹的发生和扩展行为，导致结构最终的失效，从而改变材料中韧性和断裂强度的分散性。然而，为了更深入地理解BZO力学行为的本质，需要原子尺度模拟来获取必要的微观信息[15]。DFT[16-17]计算通常用于研究小系统的静态特性，而分子动力学（MD）模拟[18-19]已被广泛用于研究更大系统的动力学特性。力场对分子动力学计算结果起决定性作用，力场的精确度决定了分子动力学模拟的精确度。BZO体系目前已考虑两体短程作用和库仑静电作用的经验力场，但力场的计算精度有待提高。

广义来讲，MD力场分为基于物理模型的“纯物理”的经验力场[20-24]和基于机器学习算法的“纯数学”的机器学习力场[25-30]。在机器学习力场出现之前，经验力场是分子动力学模拟的主导。针对各种不同的体系和不同的科学问题，研究者已经开发出各种各样的经验力场，这些经验力场凝结了前人对于模拟体系和科学问题的物理理解。经验力场的优势是可移植性较好，因为其中包含了对体系的物理描述。但这些经验力场中的物理假设缺陷在于没有完全描述体系中的所有物理本质，例如有的经验力场仅考虑了体系的两体作用和三体作用，而忽略了体系的其他多体作用，势能面计算精度较低。“纯数学”的机器学习力场不含有任何对体系的物理假设[31-34]，通过大量的拟合参数和灵活的函数形式实现了极强的表示能力，因此势能面计算精度较高。但机器学习力场最大的缺陷在于可移植性较差：对于和训练集描述的构象空间相差较大的构象，机器学习力场可能会给出误差较大的结果。所以，一个自然的想法是，能否将“纯物理”的经验力场和“纯数学”的机器学习力场的优点相结合，即实现高精度的势能面，又实现较好的可移植性。

本研究以BZO体系为例提出了一般的基于物理模型的机器学习力场开发方法。对于经验力场没有考虑到的物理作用，采用机器学习的方法进行学习，总的力场就包含了经验力场和机器学习修正项两部分。经验力场考虑了体系主要的物理作用，并且使模型具有了较好的可移植性。机器学习修正项考虑了经验力场没有考虑到的其他多体作用，提高了模型的计算精度。这样就集合“纯物理”的经验力场和“纯数学”的机器学习力场的优点，实现高精度高可移植性的力场模型开发，最后从静态性质、相稳定相和力学性质三方面对基于物理模型的机器学习力场的准确性进行了验证。

1 机器学习数据集及方法

以BaZrO3体系的静态性质和力学性质为研究目标，构造了和静态性质和力学性质密切相关的数据集，包括应变下的BaZrO3构象和沿不同方向单轴拉伸的构象。所有构象均来自于从头算分子动力学（AIMD）[35]模拟或者基于经验力场的MD模拟。详细的数据集如表1所示，该数据集共包含60000个构象。其中，（δ，δ，δ，0，0，0）应变的BaZrO3构象包含了无应变、±1%应变、±3%应变和±5%应变等不同类型，这些构象将用于学习如晶格常数、结合能以及弹性常数等静态性质；沿不同晶向单轴拉伸的构象将用于学习不同晶向的杨氏模量等力学性质。

本工作使用的经验力场来源于参考文献[36]，考虑了两体短程作用和库仑静电作用。经验力场表达式为：

式中：Uij是原子i和原子j之间的势能；rij是原子i和原子j之间的距离；qi和qj是原子i和原子j的电荷数；ϵ0为真空介电常数；Aij，ρij和Cij为原子i和原子j之间的Buckingham力场参数。

BaZrO3体系中不同类型原子之间的Buckingham力场参数如表2所示。长程的库仑静电作用采用Particle-Particle Particle-Mesh（PPPM）算法[37]求解。

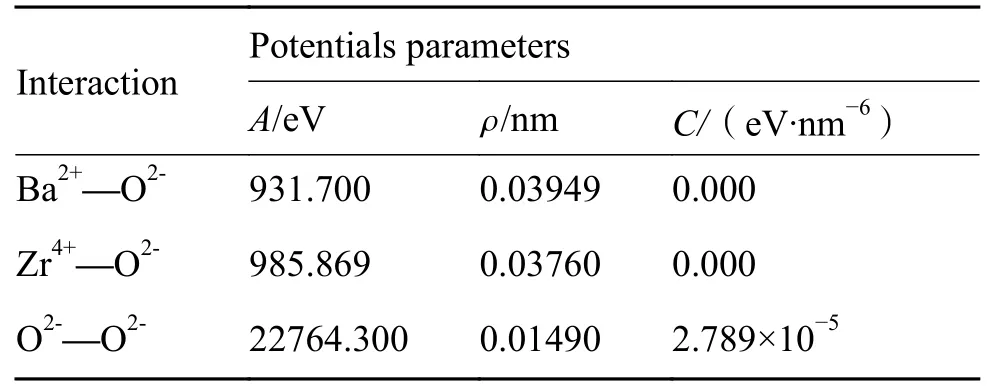
表2 BaZrO3体系中不同类型原子之间的Buckingham力场参数Table 2 Interatomic potentials parameters for BaZrO3

对于数据集中的构象，分别使用DFT和经验力场[36]计算每个构象的体系势能和原子受力，两者的差值被用做机器学习的数据集。最终的力场模型由经验力场和机器学习力场修正项构成。使用VASP软件包[38-40]进行DFT计算，计算采用增强投影波方法和Perdew-Burke-Ernzerhof泛函[41]。平面波基组的截断能设置为400 eV。所有AIMD模拟均使用了2×2×2的Monkhorst-Pack K点网格。图1给出了构建基于物理模型的机器学习力场的流程。

图1 构建基于物理模型的机器学习力场的流程Fig. 1 Workflow for constructing a machine learning force field based on a physical model

基于上述数据集，使用DeePMD[42]人工神经网络框架训练了机器学习力场。训练的截断半径为0.6 nm，批次大小设置为4，训练迭代了10万个批次。起始和终止的学习率分别设置为5×10-3和5×10-8，学习率在训练过程中指数衰减。最后，使用一个隐藏层结构为240×240×240的深度神经网络，将局部原子环境映射到原子对体系势能的贡献。训练完成后将获得基于物理模型的机器学习势。

2 结果与讨论

训练过程中训练集体系势能和原子受力的均方根误差（RMSE）随训练批次的变化如图2所示，可以看出在训练结束时体系势能和原子受力的RMSE均达到收敛状态。

图2 训练过程中训练集体系势能和原子受力的RMSE随训练批次的变化Fig. 2 Variation of RMSE of potential energy and atomic forces on training set against training batches during training

图3为数据库和机器学习力场的体系势能和原子受力之间的比较。训练集和测试集的体系势能RMSE分别为2.09 meV/atom和1.99 meV/atom。对于原子受力，训练集和测试集的RMSE分别为1182.99 meV/nm和1180.99 meV/nm。机器学习力场的RMSE值与机器学习模型的典型RMSE值一致[43]。

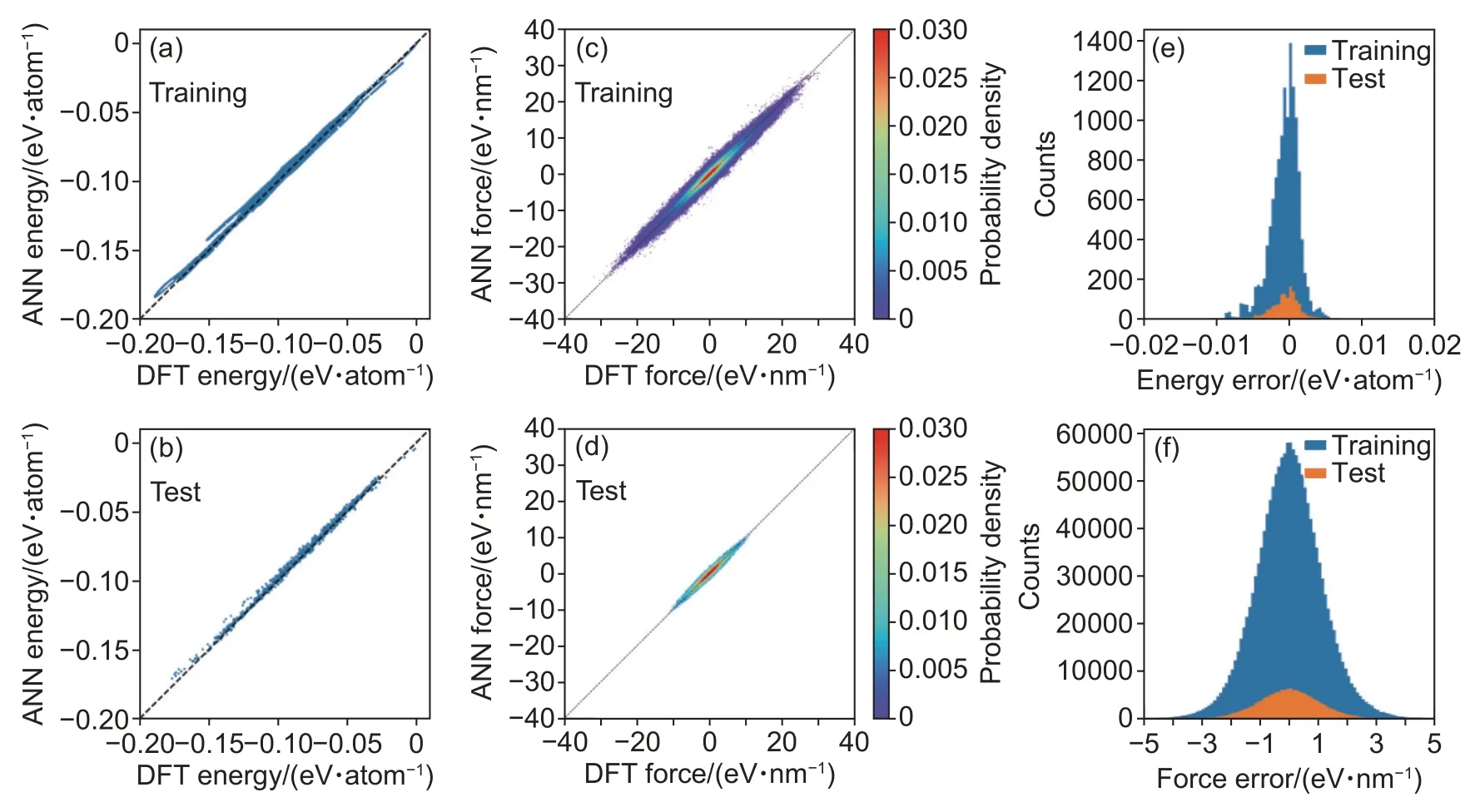
图3 机器学习力场计算结果和密度泛函理论参考数据的比较 （a）训练集每个原子平均能量的比较；（b）测试集每个原子平均能量的比较；（c）训练集上各个原子受力的比较；（d）测试集上各个原子受力的比较；（e）训练集每个原子的平均能量和各个原子受力的分布；（f）测试集每个原子的平均能量和各个原子受力的分布Fig. 3 Comparisons of machine learning potential results with respect to the references of DFT data （a） comparison of average energy per atom for training set；（b） comparison of average energy per atom for test set；（c）comparison of forces on individual atoms on a training set；（d）comparison of forces on individual atoms on test set；（e） error distributions for energies and forces for training set；（f）error distributions for energies and forces for test set

为了验证基于物理模型的机器学习力场的准确性，计算了静态性质，并和DFT理论计算结果进行了比较。这里的静态性质包括晶格常数a，弹性常数C11、C12和C44。详细的结果如表3所示。同时，还给出了经验力场和直接学习训练集数据得到的纯机器学习力场的结果。

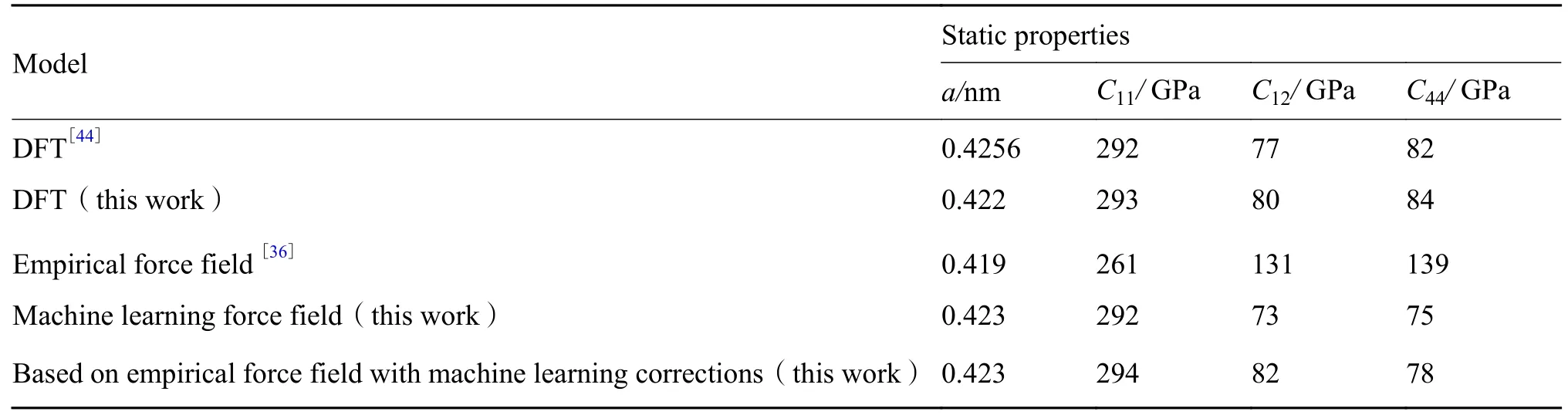
表3 基于物理模型的机器学习力场的静态性质和DFT理论计算结果的比较Table 3 Comparison of static properties based on empirical force field with machine learning corrections and DFT references

从表3可知，本研究的DFT计算结果与其他DFT工作结果一致。另外，无论是基于物理模型的机器学习力场还是纯机器学习力场，静态性质结果都接近DFT参考数据，远好于经验力场。最后，对于静态性质，基于物理模型的机器学习力场获得了和纯机器学习力场接近的结果，说明机器学习修正项可以提高经验力场计算精度，使其具有类似于纯机器学习力场的精度。

合理的力场可以使结构从不稳定转变为稳定状态。例如，将不稳定的无序结构转变为稳定的有序结构，抑或对模拟盒子施加形变后结构可以恢复原状。为了验证基于物理模型的机器学习力场的准确性，还进行了如下测试：（1）对BaZrO3体系所有原子施加一个随机的位移，构造出无序结构，然后进行能量最小化，观察结构能否转变为稳定的有序结构恢复原状；（2）对模拟盒子施加不同的应变，然后进行能量最小化，观察结构能否恢复原状。同时，还给出了经验力场和直接学习训练集数据得到的纯机器学习力场的结果。

分子动力学模拟采用LAMMPS软件包[14]，三边均采用周期性边界条件，能量最小化采用共轭梯度算法。使用径向分布函数（radial distribution function，RDF）表征结构的有序性。RDF通常指的是给定某个粒子的坐标，其他粒子在空间的分布几率，因此RDF既可以用来研究物质的有序性，也可以用来描述电子的相关性。

RDF的定义为：

式中：g(r)是径向分布函数；n(r)是半径r处，宽度为Δr内的原子总数；ρ是平均原子密度。

对原子数目为625的BaZrO3体系所有原子施加一个大小为0.053 nm（25%的O—Ba键长）的随机位移构造无序结构。图4为使用基于物理模型的机器学习力场能量最小化过程中结构和RDF的变化（图中红色为O原子，蓝色为Ba原子，黄色为Zr原子）。可以发现随着能量最小化的进行，结构逐渐从无序转变为有序，RDF的峰由低变高、由宽变窄。能量最小化结束后，体系恢复为完美的结构。

对原子数目为625的BaZrO3体系所有原子施加了从5%到30%的O—Ba键长的随机位移，分别使用经验力场、机器学习力场和基于物理模型的机器学习力场进行能量最小化，结果如表4所示。可以发现，对于20%及以内的O—Ba键长的随机位移，所有三个模型均可以使无序结构恢复到完美有序结构。但施加25%的O—Ba键长的随机位移时，机器学习力场无法使无序结构恢复到完美有序结构。最后施加30%的O—Ba键长的随机位移时，所有三个模型均无法使无序结构恢复到完美有序结构。由于训练集多数构象均位于平衡位置附近，所以机器学习力场在描述远离平衡位置的构象时可能产生较大误差，比如计算施加很大随机位移的无序构象时。但经验力场由于具有物理模型，对于这种远离平衡位置的构象仍然具有一定的有效性，因此在处理无序构象恢复为完美有序结构时具有优势。基于物理模型的机器学习力场继承了经验力场的这一优势，在这一场景中展示出了相似的结果，好于纯机器学习力场。

表4 基于不同模型的无序结构能量最小化结果Table 4 Energy minimization results for disordered structures based on different models

另外，对原子数目为625的BaZrO3体系模拟盒子施加应变，分别使用经验力场、纯机器学习力场和基于物理模型的机器学习力场进行能量最小化，结果如表5所示。可以发现，当同时压缩模型，并且改变夹角时，纯机器学习力场无法使施加应变结构恢复到完美有序结构。此时经验力场和基于物理模型的机器学习力场仍然有效。这一测试再次说明基于物理模型的机器学习力场继承了经验力场中含有物理模型的优势，能使远离平衡位置的结构恢复到平衡位置，效果好于纯机器学习力场。

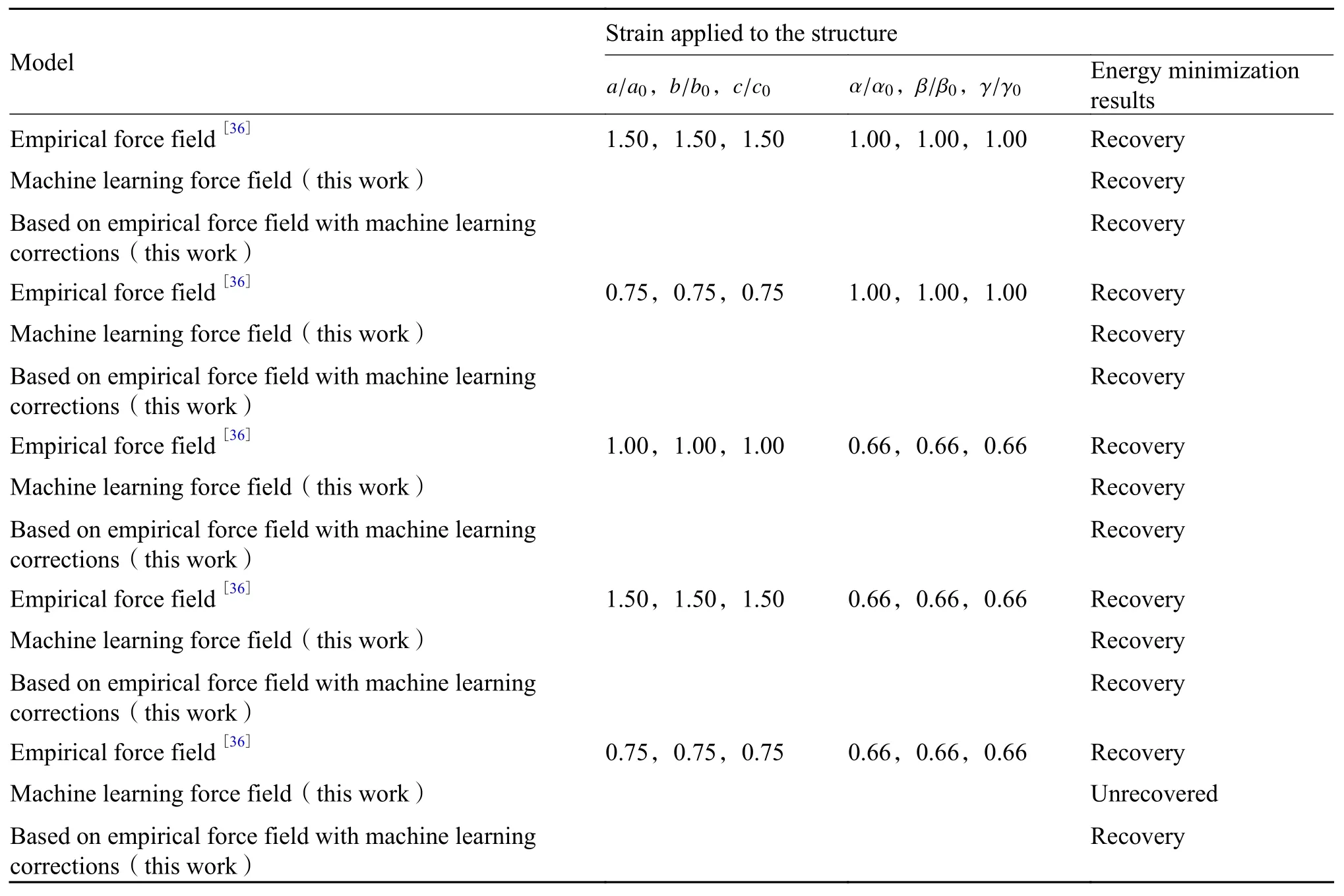
表5 基于不同模型的施加应变结构能量最小化结果（其中 为施加应变后的晶格参数，为施加应变前的晶格参数）a，b，c，α，βandγ a0，b0，c0，α0，β0andγ0 a、b、c、α、β和γa0、b0、c0、α0、β0和γ0Table 5 Energy minimization results for structures under strain based on different models（ are lattice parameters after applying strain， are lattice parameters before applying strain）

针对BaZrO3体系，研究了沿不同晶向的线弹性阶段的力学性质。表6给出了模拟体系的参数。

表6 BaZrO3模拟体系参数Table 6 Parameters of different BaZrO3 systems

分子动力学模拟采用LAMMPS软件包[14]。三边均采用周期性边界条件模拟宏观材料在单轴拉伸条件下的线弹性阶段的力学性质。拉伸过程采用NPT系综，控温算法使用Nose-Hoover热浴法[45-46]，控压算法使用Parrinello-Rahman算法[47]。时间步长取0.5 fs。体系首先使用NVT系综弛豫在300 K下弛豫50 ps，然后每10000步加载0.5%应变。

图5展示了BaZrO3模型沿不同晶向的线弹性阶段应力-应变曲线。表7所示为使用线弹性阶段的应力-应变曲线拟合得到的杨氏模量。图5（a）为模型A在300 K下沿着 [100] 方向的线弹性阶段的应力-应变曲线。图5（b）、（c）和（d）分别为模型B在300 K下沿着方向的线弹性阶段的应力-应变曲线。可以发现对于所有4个单轴拉伸晶向，机器学习力场和基于物理模型的机器学习力场结果非常接近，而两者和基于经验力场的结果存在差异。

图5 BaZrO3模型沿不同晶向的线弹性阶段应力-应变曲线Fig. 5 Stress-strain curves of BaZrO3 in linear elastic region along different crystal directions

表7 BaZrO3模型沿不同晶向的杨氏模量Table 7 Young’s modulus of BaZrO3 along different crystal directions

由表7可知，纯机器学习力场和基于物理模型的机器学习力场计算得到的杨氏模量和实验结果更接近，优于经验力场计算结果。

3 结论

（1）开发了基于物理模型的机器学习力场。首先构建了数据库，其中包含了与静态性质和力学性质相关的构象。然后对于数据集中的构象，分别使用DFT和经验力场计算了体系势能和原子受力信息。最后，使用机器学习方法来学习DFT和经验力场之间的差值。最终的模型由经验力场和一个机器学习修正项构成。

（2）分别使用经验力场、纯机器学习力场和基于物理模型的机器学习力场计算了BaZrO3的静态性质，发现纯机器学习力场和基于物理模型的机器学习力场的计算结果和DFT一致，远好于经验力场。从弹性常数C11、C12和C44的计算来看，纯机器学习力场与DFT的计算结果误差为0.34%、8.75%和10.71%，基于物理模型的机器学习力场与DFT的计算结果误差为0.34%、2.5%和7.14%。后者的误差略低于前者，说明机器学习修正项可以提高经验力场计算精度，使其具有类似于纯机器学习力场的精度。

（3）分别使用经验力场、纯机器学习力场和基于物理模型的机器学习力场研究了BaZrO3的相稳定性，发现经验力场和基于物理模型的机器学习力场在处理无序构象恢复为完美有序结构时具有优势，基于物理模型的机器学习力场继承了经验力场的这一优势，好于纯机器学习力场。

（4）分别使用经验力场、纯机器学习力场和基于物理模型的机器学习力场计算了BaZrO3的四个不同晶向的杨氏模量，发现纯机器学习力场和基于物理模型的机器学习力场结果非常接近。纯机器学习力场、基于物理模型的机器学习力场和经验力场计算结果与试验值的误差分别为9.22%、1.6%和29.06%，前两者的误差要远低于经验力场。