一类两体非X-型量子态的量子失谐
张传彬,周建明,胡晓莉
(江汉大学数学与计算机科学学院,湖北 武汉 430056)
0 引言

其中px|y为已知随机变量Y=y的条件下,随机变量X=x的条件概率.经典交互信息的另一种表达形式:
J(X,Y)=H(X)-H(X|Y),
其中H(X|Y)=H(X,Y)-H(Y).
在量子信息理论中,两体量子态ρab的量子交互信息可以表示为:
I(ρab)=S(ρa)+S(ρb)-S(ρab)
(1)
其中ρa=trb(ρab)为两体量子态ρab在b空间上的偏迹;S(ρ)=-ρlog2ρ为冯·诺依曼熵,是经典信息中香农熵在量子信息中的推广.

(2)
其中概率pk=tr(I⊗Bk)ρ(I⊗Bk),k=1,2.关于冯·诺依曼测量的条件信息被定义为:
I(ρ|{Bk})=S(ρa)-S(ρ|{Bk})
(3)

C(ρ)=sup{Bk}I(ρ|{Bk})
(4)
那么量子失谐被定义为:
Q(ρ)=I(ρ)-C(ρ)
(5)
关于两体X-型量子态的量子失谐,目前已经研究得比较深入.Luo等在2008年给出了X-型量子态量子失谐的解析解[2];Jing N等给出了一般X-型量子态量子失谐的解析解[3],但对非X-型量子态的研究较少[4].笔者考虑两体非X-型量子态的量子失谐,在两体X-型量子态[5]的基础上,扩充其研究.
1 两体非X-型量子态的量子失谐
本文中考虑下列两体非X-型量子态ρ的量子失谐,其ρ由下式给出:
(6)
其中I为2×2的单位矩阵,σ1,σ2,σ3为Pauli矩阵,都是2×2的自旋复矩阵,s1,s2,s3,c∈R.由于任意一个两体量子态都可通过酉变换落于Bloch球面上,因此我们不妨限制si,c∈[-1,1],i=1,2,3量子态ρ的4个特征值为:
众所周知,密度算子ρ应满足:①ρ的迹为1;②ρ为半正定算子.因此,特征值应满足如下条件:
(7)
(8)
因此,ρ的量子交互信息为:

(9)

(10)
(11)

(12)
(13)
(14)
由于V+σiV落在三维单位球面上,因此我们可引入新变量z1,z2,z3,且
(15)
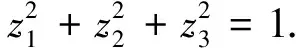
令θ=s1z1+s2z2+s3z3,则θ∈[-1,1].由(3)式、(4)式可得ρ的经典关联为:
(16)

(17)
最后,由(5)式可得ρ的量子失谐为:
(18)
定理对于(6)式中的两体非X-态ρ,其量子失谐为:
(19)

首先,求出G(θ)对θ的导数,有:
1) 当θ=0时,G′(0)=1>0;
2) 当θ>0时,(1+θ)2(1-θ)2-c2(1-θ)2>(1+θ)2(1-θ)2-c2(1+θ)2,有G′(θ)>0
因此G(θ)在θ∈[0,1]上为增函数,易知,G(θ)max=G(θmax).



最后将G(θ)max代入(18)式可得量子态ρ的量子失谐为(19)式.
2 两个实例

图1 例2中G(θ)的图
例1考虑一种特殊情况,当s1=s2=s3=0,c′=-c时,两体非X-型量子态ρ退化成Werner态:
(20)
在这种情况下,ρ的量子失谐为:
(21)
例2令s1=0.1,s2=0.2,s3=0.2,c=0.3,此时两体非X-型量子态ρ为:

其特征值为:λ1=0.4,λ2=0.342 705,λ3=0.25,λ4=0.007 294 9;图1中,给出了G(θ)关于θ的函数图像,从图中可以看出G(θ)随着θ变化而变化的曲线图形由定理可知Q(ρ)=0.611 1.
3 结论
量子失谐是两体量子态的重要量子关联之一,对任意的两体量子态不是很容易求其解析解.本文中在考虑两体非X-态的量子失谐时,发现其运算规律,求出其最优解析解,扩展了两体X-态的量子失谐问题.一般的两体量子态含有9个参数,而由于这样的量子态的特征值表达式过于复杂,导致本文中并没有解决所有两体量子态的量子失谐问题.事实上,从理论上说,带参数的四阶方阵的特征值总有其根式表达式,我们希望能找到参数之间的某种关系,使其特征值能得以化简,从而计算出更一般的两体量子态的量子失谐.

