印制板制造中量化蚀刻研究

韩雪川 王星星

（深南电路股份有限公司，广东 深圳 518117）

0 引言

高频与高速信号传输质量与印制电路板（PCB）的阻抗是否匹配有着密不可分的联系，在第5代移动通信技术（5G）大规模商用的背景下，信息传输日益趋向高频化与高速化，因此对PCB的阻抗能力提出了更严格的要求[1]-[3]。

对于PCB非电镀的内层线路而言，影响阻抗的因素主要是线路宽度（简称线宽）和介质层厚度（简称介厚）[4]-[9]。在理想的情况下，只要把线路宽度和介质层厚度做到与客户所设计的一致，就能达到阻抗匹配的目的，但是在实际生产的情况下，要把线路宽度和介质层厚度做到与客户所设计的一致是一件非常具有挑战性的事情。

目前，行业内大多是通过控制蚀刻首件的线路宽度来控制批量件的线宽[9]-[14]，其管控的首件线宽公差通常为客户设计线宽值±5%到±10%，一般做1到3次首件才能达到管控要求，而以此首件参数加工的批量件线宽分布可能偏离客户设计值的±10%，最终造成阻抗不匹配而导致批量报废事故发生。若首件线宽按照客户设计线宽值±1%控制，则往往会导致多次首件不合格而反复调整参数重做首件，造成等待浪费，并且生产效率也不理想。

基于此，本工作拟建立一套模型，在不牺牲效率、不增加经营成本的前提下，在二次首件以内将首件线宽控制在客户设计线宽中值±1%以内，从而提升批量件的线宽准确度。

1 原理及机理分析

蚀刻是控制线宽的一个关键工序。通常，一个新的料号在进行蚀刻批量加工之前都需要做首件，然后根据实际线路宽度与设计值所允许的公差范围来判断首件是否合格，合格之后再进行批量生产。否则，则需要调整生产参数，然后重做首件，直至合格。而参数的调整一般依据的是操作者的经验，为尽量降低首件的次数并减小首件线宽与设计线宽中值之间的差异，提升线宽控制准确度，本工作拟建立数学模型用于快速优化首件的蚀刻线速。

对于蚀刻制程而言，由于蚀刻机的长度是固定的，其实质是板件在蚀刻机中的有效反应时间（蚀刻线速）的变化引起线宽的变化。那么通过实验就可以得到不同的有效反应时间的对应的线宽变，通过函数拟合就可以得到时间与线宽的函数关系式，再对此函数进行求导就可以得到线宽变化速率。当没有光致抗蚀层阻挡的铜面区域，其铜面蚀刻速率较快，线宽变化速率也很快；当蚀刻到一定深度后，光致抗蚀层对铜面有保护作用，蚀刻速率较慢，线宽变化速率也很慢。现把光致抗蚀层宽度与线路宽度之差称为膜线差。

图1、图2展示了线宽变化量、反应时间变化量、线宽变化速率之间的关系。线宽变化速率在有效反应时间变化量上的累积就是需要达到的线宽的变化量（如图1、图2△S所示）；批量件的线宽理论上应与设计值一致，因此目标膜线差在蚀刻之前就已经确定了，线宽的变化率也是确定的。因此只需要知道第一次首件状态的线宽变化速率就可以得到首件到批量件的有效反应时间变化量，而第一次首件的线宽变化速率可以通过光致抗蚀层与实测首件线宽差确定；最终蚀刻机有效长度除以有效时间变化量与首件有效反应时间之和即为最优首件蚀刻线速也即批量件的蚀刻线速（下述统称批量件蚀刻线速）。

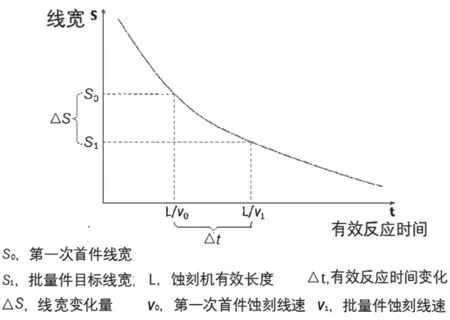
图1 线宽与有效反应时间的关系图

图2 线宽变化速率与有效反应时间的关系图（可由图1求导得到）

2 模型的建立

设第一次首件在蚀刻机中的有效反应时间为t0，设蚀刻机的有效长度为L，设首件的蚀刻线速为V0，如式（1）所示：

图3、图4所示为批量件光致抗蚀层宽度与线路宽度的状态，设此状态对应的线宽为S1（S1在理想状态下是线宽设计值），光致抗蚀层宽度与批量件实测线宽的差值为α1，如式（2）所示：

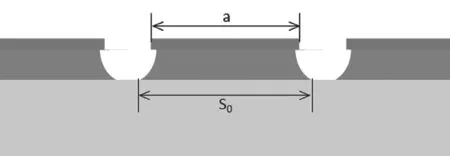
图3 第一次首件光致抗蚀层宽度与线路宽度的状态

图4 调整后批量件光致抗蚀层宽度与线路宽度的状态

设批量件对应的蚀刻线速为V1，设批量件在蚀刻机中的有效反应时间为t1，设批量件相对于第一次首件其有效反应时间的变化量为，如式（3）所示：

其中，V1是本模型最终需要求的量。设线宽变化的速率为k，如式（4）所示：

当第一次首件时对应的线宽变化速率为K0，设批量件时对应的线宽变化速率为K1。从第一次首件到批量件，其平均的线宽变化速率如式（5）所示：

如取HVLP覆铜板11块，表面铜厚15 μm，经表面清洁后贴干膜，干膜厚度30 μm，然后经过LDI（激光直接成像技术）曝光绘制成线路110 μm、间距110 μm的光致抗蚀图形。分别对曝光后的覆铜板进行显影、蚀刻、退膜。其中显影和退膜的参数一致，11块板件对应不同蚀刻线速，经蚀刻后分别测量每块板件对应的线宽，每块板件对应的取样点≥25个，以平均值作为最终的线宽，并得到对应的膜线差。蚀刻机的有效长度L为4.7 m，因此不同蚀刻线速有对应的反应时间，有关数据见表1。

将反应时间对应的线宽进行函数拟合，得到拟合方程为式（6）所示：

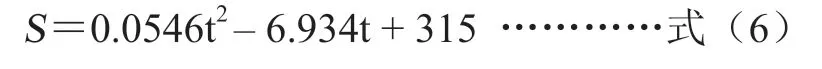
其中S代表线宽，t代表有效反应时间。对式子（6）进行求导，得到线宽变化速率函数如式（7）所示：

不同的蚀刻机以及不同铜厚的板件其表达式可能不同，但建立该式子的方法相同。将反应时间（表1数据）分别代入到式（7）中得到不同的k，然后将k和膜线差（表1数据）进行函数拟合，得到表达式见式（8）所示：

表1 线路蚀刻数据表

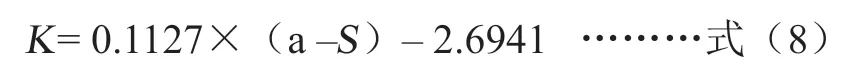
第一次首件状态的线宽变化速率，见式（9）所示：

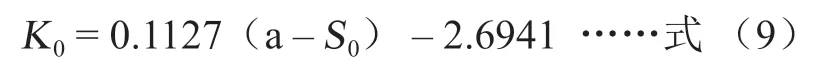
批量件的线宽变化速率，见式（10）所示：

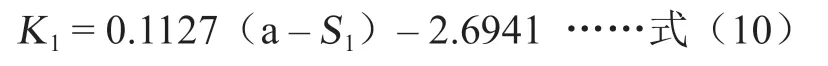
通过式（1）～式（10）可得式（11）～式（13）。

其中，a，S1在蚀刻之前就已确定，V0、S0在第一次首件后确定，L的有效长度是固定不变的，本论文中L为4.7 m，因此式（11）式（12）中只有一个未知数V1，V1即所预测的批量件的蚀刻线速。

此模型是根据第一次首件线宽与设计线宽的差值对蚀刻线速进行量化调整，因此，我们称此模型为量化蚀刻模型。

3 蚀刻模型验证

为了验证该模型用于首件线宽调整的有效性，随机抽取了5个料号进行了测试，铜箔厚度均为约15 μm。经贴膜、曝光、显影、蚀刻后分别用自动线宽测量仪测量每个料号，第一次首件的最小线宽（测量10个以上不同的位置，取均值），将首件线宽均值超出设计值1%的料号通过模型给出的预测蚀刻线速[以式（11）、式（12）计算]进行生产，然后再对板件的最小线宽进行测量（测量10个以上不同的位置，取均值），线宽测量结果如表2所示。

表2 蚀刻模型验证结果表

从实际的实验结果来看，模型调整后的线宽平均值与设计值的差值均维持在1 μm以内，所以这个模型是可以接受的。若第一次首件线宽均值与设计线宽相差较大，则可能需要多次首件来迭代。

4 自动化方案拟实现步骤

从通过扫码自动调取首件配方参数，到蚀刻机执行经模型调整后的线速进行批量生产，步骤见图5所示。

图5 量化蚀刻模型自动化方案拟实现步骤图

6 结论与展望

本项目建立了一套量化蚀刻模型，该模型经过验证能够有效地实现对PCB线宽的精确控制。该模型通常根据1次首件调整线速后就能使批量线宽达到合格，提升阻抗的匹配度；同时可以节约人力资源和设备资源的大量等待时间，提高生产效率。该模型配合自动化方案，可以全程实现自动化，以进一步地提升生产效率。

本论文所提出的模型是基于本公司内部的蚀刻设备及加工方法所建立的，不同的蚀刻设备、不同铜厚的板件可能存在不同的模型，但仍然可以根据本论文所提出的方法重新建立模型。同时，该模型对于外层线路宽度的控制也有一定的参考意义。