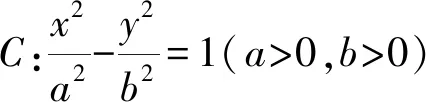对一道椭圆联考题的深度探究
付增民
(永康市第一中学,浙江 永康 321300)
三点共线问题是数学中的重要题型之一,而圆锥曲线中的三点共线问题则是高考及各地模拟考试考查的重点,如2021年新高考Ⅱ卷的第20题考查的就是以椭圆为载体的三点共线充要条件的证明[1].
1 考题呈现

(1)求椭圆C的方程;

2 考题解析
解析(1)设椭圆C的焦距为2c(0 解得a2=3,b2=1. (2)从充分性和必要性两个方面进行证明. 必要性:若M,O,N三点共线,不妨设A(x0,y0),M(x1,y1),N(-x1,-y1). 又因为A(x0,y0),M(x1,y1)都在椭圆C上, ① ② ①②两式相减,得 充分性:设A(x0,y0),M(x1,y1),N(x2,y2),则 ① ② ①②两式相减,得 所以A(x0,y0),M′(-x1,-y1),N(x2,y2)三点共线. 又因为点M′(-x1,-y1)在椭圆上,所以点M′(-x1,-y1)与点N(x2,y2)重合,显然点M(x1,y1)与点M′(-x1,-y1)关于原点O对称, 所以弦MN过原点O,即M,O,N三点共线.充分性得证. 点评该联考试题题意简明,解答思路清晰,主要考查直线与椭圆的位置关系,考查分析问题和解决问题的能力.(1)根据题意,利用待定系数法求得椭圆的方程;(2)从充分性和必要性两个方面,运用“设而不求”“点差法”和“对称性”等手段,利用斜率关系进行证明,体现解析几何问题的本质就是将几何问题转化为代数问题,通过代数运算研究几何图形性质,图形问题代数化是解析几何的本质. (1)求椭圆C的方程; 点评上面联考题与该高考题本质上可谓如出一辙,第(1)小题所求椭圆方程相同,第(2)小题的设问形式和背景一致.这就启示我们在高考复习教与学的过程中重视“回归”,即回归到对往年高考真题的深层次挖掘和研究,并将这样的“回归”贯穿复习备考的始终. 若将上述联考题第(2)小题证明的充要条件分别按充分条件和必要条件来命题,可有下面的两个变式. (1)求椭圆C的方程; (1)求椭圆C的方程; 若将上述联考题中的椭圆类比到双曲线,则有: (1)求双曲线C的方程; 解析(1)设C的焦距为2c(0 解得a2=3,b2=1. (2)从充分性和必要性两个方面进行证明. 必要性:若M,O,N三点共线,不妨设A(x0,y0),M(x1,y1),N(-x1,-y1). 又因为A(x0,y0),M(x1,y1)都在双曲线C上, ③ ④ ③④两式相减,得 充分性:设A(x0,y0),M(x1,y1),N(x2,y2), ③ ④ ③④两式相减,得 所以A(x0,y0),M′(-x1,-y1),N(x2,y2)三点共线. 又因为点M′(-x1,-y1)在双曲线上,所以点M′(-x1,-y1)与点N(x2,y2)重合,显然点M(x1,y1)与点M′(-x1,-y1)关于原点O对称, 所以弦MN过原点O,即M,O,N三点共线.充分性得证. 同椭圆一样,若将变式3第(2)小题证明的充要条件分别按充分条件和必要条件来命题,可有下面的两个变式. (1)求双曲线C的方程; (1)求双曲线C的方程; 我们能否将上述联考题及与双曲线的类比变式题推广、延伸到有心圆锥曲线的一般情形呢?回答是肯定的!现延伸到椭圆和双曲线的一般情形,推广得到一般性命题. 类比椭圆的结论可以得到双曲线的相应结论. 两个命题的证明可以按照上述联考题及与双曲线的类比题的证明过程分别进行,这里从略,有兴趣的读者不妨自行完成. 许多典型的数学问题,其中蕴含的背景或规律需要挖掘或推广延伸,因而我们平时的解题:一是要重视问题的变式,通过变式去从“变”的现象中发现“不变”的本质,从“不变”中探求规律;二是适宜地将问题推广延伸为一般性的结论用于解决相关问题.唯有如此,才能逐步培养学生灵活多变的思维品质,提高其数学核心素养,培养其探索精神和创新意识,从而真正把对能力的培养落到实处.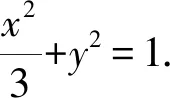
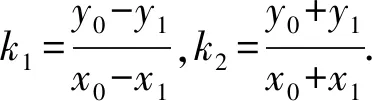
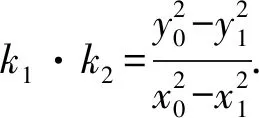


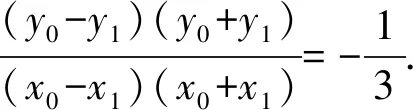

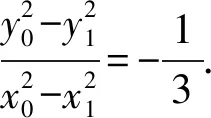
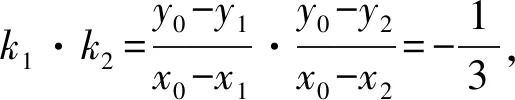


3 考题溯源



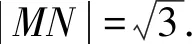

4 考题变式




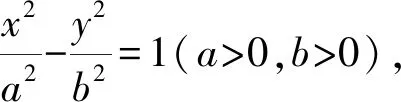


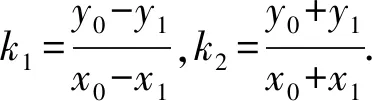
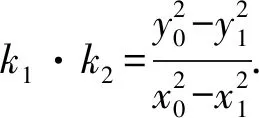
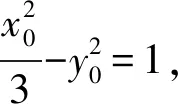
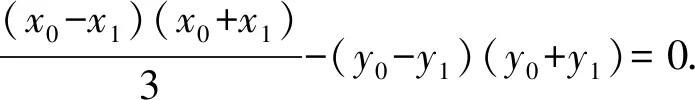
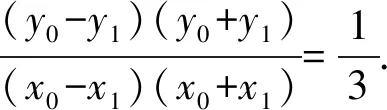

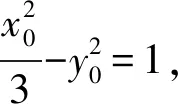

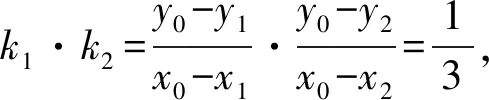


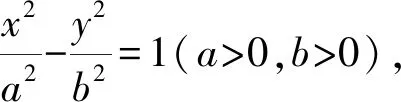
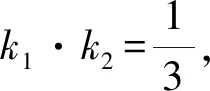
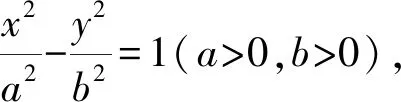

5 推广延伸