直接有限环的新刻画

赵旭东， 王 姗， 魏俊潮

(1.运城师范高等专科学校 数计系， 山西 运城 044000； 2.扬州大学 数学科学学院， 江苏 扬州 225002)

2019年第十届全国大学生数学竞赛决赛(数学类， 三、 四年级)第五大题：

设R为结合环，a,b∈R， 若a+b=ab， 且关于x的方程

(1)

在R中有解， 则ab=ba.

证明由于该方程组等价于方程组

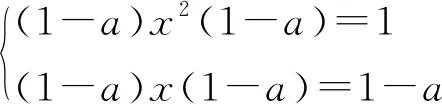
再注意到a+b=ab等价于(1-a)(1-b)=1, 故

(1-a)x=(1-a)x[(1-a)x2(1-a)]

=[(1-a)x(1-a)]x2(1-a)

=(1-a)x2(1-a)=1，

x(1-a)=[(1-a)x2(1-a)]x(1-a)

=(1-a)x2[(1-a)x(1-a)]

=(1-a)x2(1-a)=1，

因此 1-a可逆且(1-a)-1=x， 而且

x=x(1-a)(1-b)

=(1-a)-1(1-a)(1-b)=1-b.

从而 (1-b)(1-a)=x(1-a)

=1=(1-a)(1-b)， 于是ab=ba.

受此题启发， 下面给出直接有限环的几个刻画.有关直接有限环的研究可参见文献[6-9]. 本文中R均指有单位元的结合环.

定理1R为直接有限环当且仅当对任意的a,b∈R满足ab=a+b时， 有ab=ba.

证明先证必要性.假设a,b∈R， 满足

ab=a+b， 则(a-1)(b-1)=1， 由于R为直接有限环， 故(b-1)(a-1)=1， 从而a+b=ba， 所以ab=ba.

再证充分性.任取x,y∈R， 满足xy=1.记

a=x+1，b=y+1， 则(a-1)(b-1)=xy=1，

所以ab=a+b.由题设知ab=ba， 故有

(x-1)(y-1)=(y-1)(x-1)，

计算得yx=xy=1, 因此R为直接有限环.

定理2R为直接有限环当且仅当对任意的a,b∈R满足ab=a+b时关于x的方程组(1)有解.

证明先证必要性.假设R为直接有限环且对任意的a,b∈R满足ab=a+b， 则 (a-1)(b-1)=1， 故 (b-1)(a-1)=1， 从而a-1为可逆元， 故x=(a-1)-1=b-1为方程组(1)的解.

再证充分性.设u,v∈R， 满足uv=1.记

a=u+1，b=v+1， 则ab=a+b.由题设知方程组(1)有解， 设解为x=d.从而有

于是1-a可逆且(1-a)d=1=d(1-a).由于(1-a)(1-b)=1-a-b+ab=1， 所以

d=d[(1-a)(1-b)]=[d(1-a)](1-b)=1-b

所以 (1-b)(1-a)=1， 即vu=1， 所以R为直接有限环.

定理3R为直接有限环当且仅当对任意的a∈R， 方程ax=a+x有解时， 解与a可交换.

证明必要性是定理1的直接推论, 下面证充分性.

设a,b∈R， 满足ab=a+b， 则ax=a+x有解x=b. 由题设知ab=ba， 故由定理1知R为直接有限环.

引理1设a,b∈R， 方程ax=a+x有解当且仅当1-a右可逆.

证明先证必要性.若ax=a+x有解， 设x=b为一个解， 则ab=a+b.

所以(1-a)(1-b)=1-a-b-ab=1， 所以1-a右可逆.

再证充分性. 若1-a右可逆， 则有c∈R， 使得(1-a)c=1， 记b=1-c， 则c=1-b.

所以(1-a)(1-b)=1， 有ab=a+b， 所以x=b为ax=a+x的解.

定理4R为直接有限环当且仅当对任意的a∈R， 1-a左可逆时，ax=a+x有解.

证明先证必要性.因为1-a左可逆， 则有c∈R， 使得c(1-a)=1.

由于R为直接有限环， 所以(1-a)c=1， 由引理1知ax=a+x有解.

再证充分性.设a,b∈R满足ba=1， 故b(1-(1-a))=1， 所以1-(1-a)左可逆， 由题设知(1-a)x=1-a+x有解， 设为x=c， 则

(1-a)c=1-a+c，

所以

(1-a)(1-c)=-c=1-c-1

[1-(1-a)](1-c)=1， 即a(1-c)=1.

所以1-c=(ba)(1-c)=b(a(1-c))=b，

所以ab=1，R为直接有限环.

定理5设a∈R， 则方程ax=a+x有幂零解当且仅当a为幂零元.

证明先证必要性.设x=b为幂零解， 即存在n≥1， 使得bn=0且有

ab=a+b

ab2=ab+b2

⋮ ⋮

abn-1=abn-2+bn-1

abn=abn-1+bn

将上面n个等式两边同时相加， 得

abn=a+b+b2+…+bn-1+bn.

注意到bn=0， 所以有

a=(-1-b-b2-…-bn-2),b=f(b)b，

f(x)=-1-x-…-xn-2.

因为f(b)b=bf(b)， 所以an=[f(b)]nbn=0， 所以a为幂零元.

再证充分性.因为a是幂零元， 即存在n≥1， 使得an=0， 易知1-a为右可逆元.由引理1知

ax=a+x有解， 设x=b为解， 即有

ab=a+b

a2b=a2+ab

a3b=a3+a2b

⋮ ⋮

an-1b=an-1+an-2b

anb=an+an-1b

将上面n个等式两边同时相加， 得

anb=a+a2+…+an-1+an+b

所以b=(-1-a-a2-…-an-2)a=f(a)a

所以bn=[f(a)]nan=0， 即b为幂零元， 因此ax=a+x有幂零解x=b.

定理6R为直接有限环当且仅当对任意的a∈R， 1-a右可逆时， 方程ax=a+x有唯一解.

证明先证必要性.由于1-a右可逆， 所以1-a可逆， 由引理1ax=a+x有解.设b，c都为解， 则ab=a+b，ac=a+c， 所以由

(1-a)(1-b)=1； (1-a)(1-c)=1.

得 1-b=(1-a)-1=1-c， 所以b=c， 从而可知解唯一.

再证充分性.设ab=1， 则1-(1-a)=a右可逆.记

1-a=c， 1-b=d，

则cd=c+d， 所以1-c右可逆且d为方程cx=c+x的解.由题设cx=c+x有唯一解.

c(dc-cd+d)=cdc-c2d+cd

=(c+d)c-c(c+d)+cd=dc

c+(dc-cd+d)=c+dc-(c+d)+d=dc

所以dc-cd+d也为cx=c+x的解， 所以

d=dc-cd+d，

所以dc=cd.

所以

(1-b)(1-a)=dc=cd=(1-a)(1-b).

所以ba=ab=1，R为直接有限环.

定理7R为直接有限环当且仅当对任意的a∈R， 方程ax=a+x有解时， 方程

x2-(ax2+x2a)+ax2a=1有解.

证明先证必要性.假设R为直接有限环且

ax=a+x有解， 由定理2得证.

再证充分性.设u,v∈R， 满足uv=1， 记

a=1-u，b=1-v， 则(1-a)(1-b)=1， 所以

ab=a+b， 所以ax=a+x有解x=b.由题设知方程x2-(ax2+x2a)+ax2a=1有解，

即(1-a)x2(1-a)=1有解x=c，

所以(1-a)c2(1-a)=1，

所以(1-a)c2=(1-a)c2(1-a)(1-b)=1-b， 所以(1-b)(1-a)=(1-a)c2(1-a)=1，

即vu=1， 因此R为直接有限环.

下面的推论1简化了2019年第十届全国大学生数学竞赛决赛(数学类， 三、 四年级)第五大题的题设.

推论1设a,b∈R满足ab=a+b， 若x2-(ax2+x2a)+ax2a=1有解， 则ab=ba.

证明设x=c为x2-(ax2+x2a)+ax2a=1的解， 则(1-a)c2(1-a)=1.

因为ab=a+b， 则(1-a)(1-b)=1，

所以(1-a)c2(1-a)(1-b)=1-b， 即

(1-a)c2=1-b，

所以(1-b)(1-a)=(1-a)c2(1-a)=1，

所以ba=b+a=a+b=ab.