形式各异殊途同归——六个角度研究切线问题

卢会玉

(西北师范大学附属中学,甘肃 兰州 730070)

高考中,曲线的切线问题几乎成为必考内容,有时以圆为载体出现在小题,有时在填空题中直接求某函数的切线,有时以关键形式出现在大题中.一般情况下,直线与曲线相切会涉及到三个量:直线、曲线、切点;直线与圆相切也涉及到三个量:直线、圆、点.因此,切线问题都有共同的命题方式:知“二”求“一”,即知道其中的两个量去求另外一个量,虽然考查的知识点和呈现形式不同,但思维方式基本相同.

1 已知曲线的方程、切点坐标求切线方程

例1 曲线y=2sinx+cosx在点(π,-1)处的切线方程为( ).

A．x-y-π-1=0 B．2x-y-2π-1=0

C．2x+y-2π+1=0 D．x+y-π+1=0

解析因为y′=2cosx-sinx,

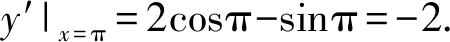
则y=2sinx+cosx在点(π,-1)处的切线方程为y-(-1)=-2(x-π),即2x+y-2π+1=0．

注本题考查利用导数工具研究曲线的切线方程,渗透了直观想象、逻辑推理和数学运算素养．采取导数法,利用函数与方程思想解题．学生易在非切点处直接求导数而出错,首先证明已知点是否为切点,若是切点,可以直接利用导数求解;若不是切点,设出切点,再求导,然后列出切线方程[1]．

例2经过点M(3,0)作圆x2+y2-2x-4y-3=0的切线l,则l的方程为( ).

A．x+y-3=0 B．x+y-3=0或x=3

C．x-y-3=0 D．x-y-3=0或x=3

解析因为x2+y2-2x-4y-3=0,

所以(x-1)2+(y-2)2=8.

当过点M(3,0)的切线存在斜率k,切线方程为y=k(x-3),即kx-y-3k=0.

解得k=1.

即切线方程为x-y-3=0.

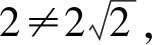
因此切线方程为x-y-3=0.故选C.

注本题考查了求圆的切线.本题实际上是过圆上一点求切线,所以只有一条.解答本题时,设直线l存在斜率k,点斜式设出方程,利用圆心到直线l的距离等于半径求出斜率k,再讨论直线l不存在斜率时,是否能和圆相切,如果能,写出直线方程,综合求出切线方程.

2 已知曲线的方程、切线方程求切点坐标

例3在平面直角坐标系xOy中,点A在曲线y=lnx上,且该曲线在点A处的切线经过点(-e,-1)(e为自然对数的底数),则点A的坐标是____．

解析设点A(x0,y0),则y0=lnx0.

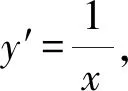
即x0lnx0=e.

令H(x)=xlnx,当x∈(0,1)时,H(x)<0,当x∈(1,+∞)时,H(x)>0,且H′(x)=lnx+1,当x>1时,H′(x)>0,H(x)单调递增,注意到H(e)=e,故x0lnx0=e存在唯一的实数根x0=e,此时y0=1,故点A的坐标为(e,1).

例4若曲线y=xlnx上点P处的切线平行于直线2x-y+1=0,则点P的坐标是____．

注导数运算及切线的理解应注意的问题:一是利用公式求导时要特别注意除法公式中分子的符号,防止与乘法公式混淆;二是直线与曲线公共点的个数不是切线的本质,直线与曲线只有一个公共点,直线不一定是曲线的切线,同样,直线是曲线的切线,则直线与曲线可能有两个或两个以上的公共点．

3 已知切线方程、切点坐标求曲线方程

例5已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a=____.

所以y=x+lnx在点(1,1)处的切线方程为

y=2x-1.

又切线与曲线y=ax2+(a+2)x+1相切,当a=0时,y=2x+1与y=2x-1平行,故a≠0.

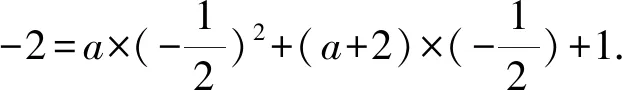
所以a=8.

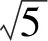
C．(x-5)2+y2=5 D．(x+5)2+y2=5

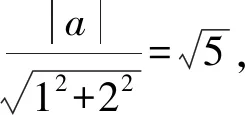
所以圆O的方程为(x+5)2+y2=5．

注切线问题应注意区分曲线在某点处的切线和曲线过某点的切线.曲线y=f(x)在点P(x0,f(x0))处的切线方程是y-f(x0)=f′(x0)(x-x0).求过某点的切线方程,需先设出切点坐标,再依据已知点在切线上求解.

4 曲线的切线与函数性质的综合问题

例7设函数f(x)=x3+(a-1)x2+ax,若f(x)为奇函数,则曲线y=f(x)在点(0,0)处的切线方程为( ).

A．y=-2xB．y=-xC．y=2xD．y=x

解法1因为函数f(x)=x3+(a-1)x2+ax为奇函数,所以f(-x)=-f(x).

所以(-x)3+(a-1)(-x)2+a(-x)=-[x3+(a-1)x2+ax].

所以2(a-1)x2=0.

因为x∈R,所以a=1.

所以f(x)=x3+x.

所以f′(x)=3x2+1.

所以f′(0)=1.

所以曲线y=f(x)在点(0,0)处的切线方程为y=x．故选D．

解法2因为函数f(x)=x3+(a-1)x2+ax为奇函数,所以f(-1)+f(1)=0.

所以-1+a-1-a+(1+a-1+a)=0.

解得a=1.

所以f(x)=x3+x.

所以f′(x)=3x2+1.

所以f′(0)=1.

所以曲线y=f(x)在点(0,0)处的切线方程为y=x．

5 曲线的切线与两直线位置关系相结合的问题

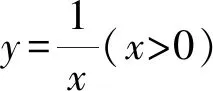
解析因为y=ex,所以y′=ex.

所以曲线y=ex在点(0,1)处的切线斜率

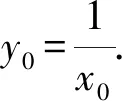
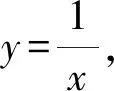
因为x0>0,所以x0=1.

所以y0=1,即点P的坐标是(1,1).

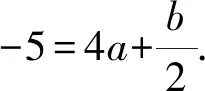
①

②

由①②解得a=-1,b=-2.

所以a+b=-3．

6 圆的切线与圆锥曲线相结合的综合问题

(1)求椭圆的离心率;

由题意,F(-c,0),则直线l的方程为

7x2+6cx-13c2=0.

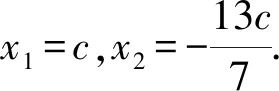
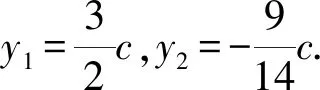
由圆心C在直线x=4上,可设C(4,t).

因为OC∥AP,且由(1)知A(-2c,0).

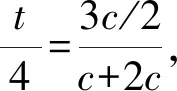
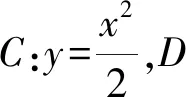
(1)证明:直线AB过定点;

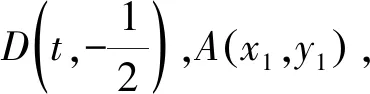
设B(x2,y2),同理可得2tx2-2y2+1=0.

故直线AB的方程为2tx-2y+1=0.

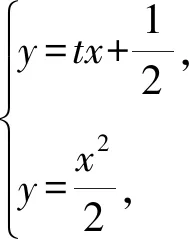
于是x1+x2=2t,x1x2=-1,y1+y2=t(x1+x2)+1=2t2+1,

=2(t2+1).

设d1,d2分别为点D,E到直线AB的距离,则

因此,四边形ADBE的面积

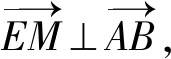
注以上题型都是圆的切线与圆锥曲线的综合问题,主要考查椭圆、双曲线、抛物线的标准方程和几何性质、直线方程、圆等基础知识.基本是以圆为主,以圆锥曲线为辅的中档题目.考查学生用代数方法研究圆锥曲线性质的能力,考查运算求解能力,以及用方程思想、数形结合思想解决问题的能力[2].

事实上,还有相当多的与切线有关的问题本文并未涉及到,但是,各种各样的切线问题所采用的解决办法具有相同和相通的地方,在一定程度上也可达到触类旁通的效果.