圆锥曲线的性质及推广运用
翁其明
(福建省平潭岚华中学,福建 福州 350400)
解析几何的重要内容就是圆锥曲线,并用代数的方法解决此类问题,也是高考数学考查的重难点,本文将从三个方面来阐述圆锥曲线的性质并做到举一反三.
1 圆锥曲线的性质
1.1 椭圆
(1)概念:平面内的任意一点M到两个固定的点F1,F2的距离之和等于常数(大于|F1F2|)的点的运动轨迹,有|MF1|+|MF2|=2a.

1.2 双曲线
(1)概念:平面内的任意一点P到两个固定的点F1,F2的距离之差等于非零常数(小于|F1F2|)的点的运动轨迹,有||PF1|-|PF2||=2a,其中由分子x2,y2对应的分母的正负确定焦点的位置.

1.3 抛物线
(1)概念:平面内到定点F和定直线l(不经过点F)的距离相等的点的运动轨迹,其中焦点的位置由一次项对应的变量决定.
(2)标准方程:y2=2px(p>0)(焦点在x轴正半轴),y2=-2px(p>0)(焦点在x轴负半轴),x2=2py(p>0)(焦点在y轴正半轴),x2=-2py(p>0)(焦点在y轴负半轴).
2 圆锥曲线的性质应用
2.1 求解三角形面积问题


图1 例1图
解析设|PF1|=r1,|PF2|=r2,
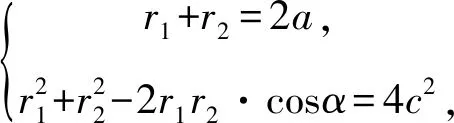
①
②
①2-②,得2r1r2(1+cosα)=4(a2-c2).
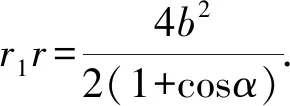


解析依据定义有|PF1|-|PF2|=2a=2.
由|PF1|∶|PF2|=3∶2,
得|PF1|=6,|PF2|=4.
又|F1F2|2=(2c)2=4×13=52,
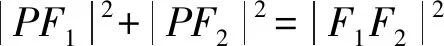
所以cos∠F1PF2=0.即PF1⊥PF2.

2.2 求解离心率问题
例3如图2,椭圆上的点P和左焦点F1,右顶点A和上顶点B,当PF1⊥AF1,PO∥AB时,求椭圆的离心率.

图2 例3图

因为PO∥AB,所以kPO=kAB.

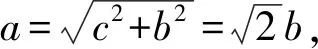


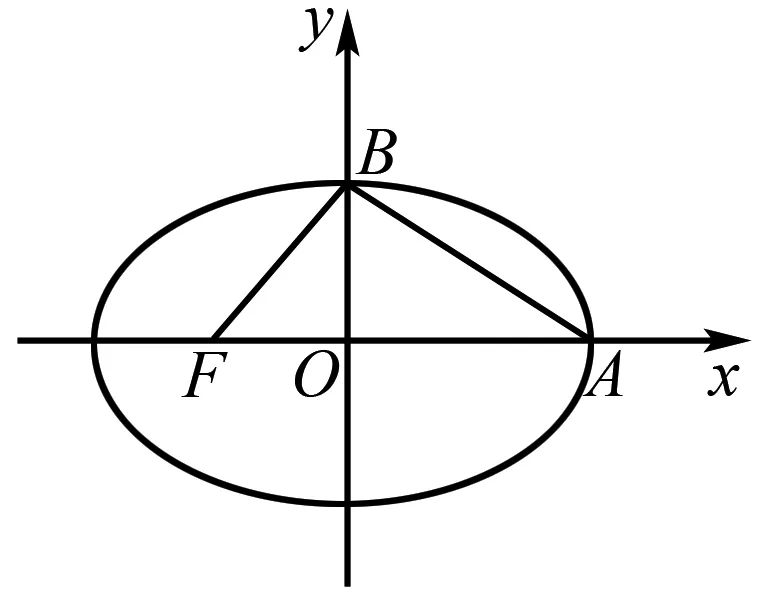
图3 例4图
解析由题知A(a,0),B(0,b),F(-c,0),
因为AB⊥BF,所以kAB·kBF=-1.

利用b2=a2-c2,代入消掉b2,得
c2+ac-a2=0.



2.3 求解圆锥曲线的最值问题
例5如图4,已知抛物线方程y2=4x,焦点为F,定点A(5,3),若点P在抛物线上运动,则|AP|+|PF|的最小值为____.

图4 例5图
解析点P在准线上的射影为D,由已知得|PF|=|PD|.
所以|AP|+|PF|=|AP|+|PD|.
即当D,P,A共线时,|AP|+|PF|取得最小值.
抛物线的准线方程为x=-1,
所以|AP|+|PD|=|AD|=5-(-1)=6.
所以(|AP|+|PF|)min=6.

解析设A(x1,y1),则由椭圆的对称性得B(-x1,-y1).
则S△ABF=S△AOF+SBOF
=|OF|·|y1|.
因为|y1|≤b,所以S△ABF≤bc.
所以(S△FAB)max=bc.
2.4 圆锥曲线光学性质的应用


图5 例7图
(1)求证:|F1P|·|F2P|为定值
(2)求P1,P2的轨迹方程
解析(1)设Q为切点,由椭圆光学性质得∠F1QP1=∠F2QP2,设为α,则
|F1P1|=|F1Q|sinα,|F2P2|=|F2Q|sinα,
所以|F1P1|·|F2P2|=|F1Q|·|F2Q|sin2α.
又∠F1QF2=180°-2α,则在ΔF1QF2中,|F1F2|2=|F1Q|2+|F2Q|2-2|F1Q|·|F2Q|cos(180°-2α)=(|F1Q|+|F2Q|)2-2|F1Q|·|F2Q|(1-cos2α)=(2a)2-2|F1Q|·|F2Q|[1-(1-2sin2α)]=4a2-4|F1Q|·|F2Q|sin2α=4a2-4|F1P1|·|F2P2|.
则4|F1P1|·|F2P2|=4a2-|F1F2|2=4a2-4c2=4b2.
所以|F1P|·|F2P1|=b2为常数,即为定值[2].
(2)设点O在CD上的射影为点M,则OM是直角梯形F1F2P2P1的中位线,于是有

在Rt△OP1M中,|OP1|2=|MP1|2+|OM|2
同理|OP|2=a2.
所以F1,F2的轨迹是以O为圆心,a为半径的圆,方程为x2+y2=a2.
综上,本文共阐述了四大类解决圆锥曲线的相关问题,此类解题方法帮助学生加强对圆锥曲线的学习,并能更加有效地帮助学生打开解决此类问题的思路.

