关于三点共线向量式的教学与解题探讨

王加成

(陕西省白河高级中学,陕西 安康 725801)

高考中,通过考查向量间的相互表示可考查学生对向量的加、减、数乘运算的掌握情况,亦可考查学生对平面向量基本定理、共线向量定理的理解程度.此时,紧抓基底能解决相关的问题,但遇到三点共线向量时,使用三点共线向量式解题会更为简便.

在人民教育出版社A版2019年6月第1版数学必修第二册教课书26页中有如下一道例题:

图1 三点共线图

笔者看到本题,很是熟悉,与北京师范大学出版社2014年7月第8版数学必修四第84页例3属于同一道题(仅仅字母变了,题意一样,结论一样).旁注里写到:“例3给出了判断三个点共线的一个方法”.

在人民教育出版社B版2020年7月第一版数学必修第二册教课书第155页也有一道相似的例题.

在不同版本的新老教材中均出现此题目,笔者认为此题想说明以下两个道理.

道理1从直线外一点指向同一条直线上不同三点的三个向量,可用任意两个向量线性表示另一向量,且系数之和为1.

道理2若三个向量共起点,一个向量可用其余两个向量线性表示,且系数之和为1,则这三个向量的终点共线.

但是教材上给的题目较为抽象,如何让学生体会到编者的用意?成为了教学中要考虑的一个问题.为此,笔者学习了参考文献[1],文中探寻了教材根源,对三点共线向量式有所拓展,并通过举例说明了拓展的应用,文献[2]阐述了利用线段定比分点解决三点共线问题,并通过例题说明相关知识的应用.两文均未提及教材中的该例题,也未提及学生如何理解熟记该公式,亦未提如何经济实惠使用该公式.由此,笔者对本题产生了以下疑惑与思考,不妥之处,敬请各位老师和读者朋友斧正[1][2].

笔者认为在讲解本题之前,让学生探究以下三个问题,会更利于理解上述例题的含义,更容易明白例题所想表明的道理.

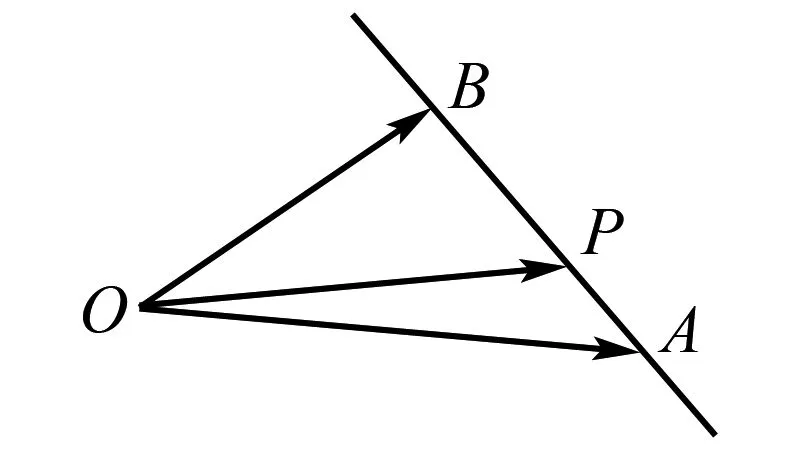
图2 问题1图

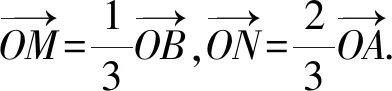
图3 问题1解法2图

通过问题1、问题2、问题3的探究,学生会发现道理1,那么这个道理是必然还是偶然?我们再将问题抽象,即自然生成课本上的例题.此时,学生就能用问题1中的“解法1”来求解课本上例题,从而发现道理1是正确的.学生能否利用“解法2”来构造出相应的平行四边形呢?笔者认为对大部分学生而言依然有难度,仍需教师的鼓励指点(如图4).但是此时的学生已理解课本上例题想说明的两个道理,也更会使用相关的结论.

图4 道理2解释图

学生可利用向量的相互表示及共线向量判定定理证明如下:

由此,可以说明道理2也正确.

图5 人教A版39页练习3

解得m+n=2.

因为N,O,M三点共线,

消λ并化简,得m+n=2.

A.3m-2nB.-2m+3n

C.3m+2nD.2m+3n

解析如图6,因为BD=2DA,

图6 2022年新高考Ⅰ卷第3题图

故选B.

三点共线向量式虽由向量共线定理衍生,但在解决共线问题更有优势,其本质是线段的定比分点问题.我们在教学时让学生从特殊到一般,逐步发现、体会三点共线的向量式会更利于学生掌握相关知识,通过有梯度的少数例题即可能达到熟练运用,从而摆脱题海.