经历愤悱过程,发展数学思维
贾富华
摘 要:小学数学教师们虽然已经普遍接受了启发式教学的思想,但如何在教学中实施启发式教学仍然存在不少困惑.本文以“鸡兔同笼”的教学为例,阐述如何在小学数学教学中实施启发式教学,让学生经历“愤”、“悱”的过程,从而发展数学思维、洞察数学的本质和感悟数学的思想方法.
关键词:启发式教学;数学思维;鸡兔同笼
《论语·述而》中记载孔子关于启发式教学的阐述.原文为“不愤不启,不悱不发”.意思是说:不到学生想弄明白,而仍然想不透时,教师先不要去开导他;不到学生心里明白,却又不能完整表达出来时,教师也先不要去启发他.宋代学者朱熹进一步解释道:“愤者,心求通而未得之意也;悱者,口欲言而未能之貌也”、“启,谓开其意;发,谓达其辞”.这就是启发式教学.而如何在教学中采用启发式教学?本文以“鸡兔同笼”为例,试图在该课的教学中阐释启发式教学的具体过程,以期为小学数学的教学提供参考.
1 留足时间,让学生经历“愤”的过程
《义务教育数学课程标准(2022版)》指出:学生是数学学习的主人,教师是数学学习的组织者、引导者和合作者.教师要充分相信学生,给学生足够多的时间和空间,让学生充分经历“愤”的过程.教师则需在学生“愤”的时候,顺势而“启”,引导他们在观察分析、独立思考、合作交流、自主探究的过程中,参与知识的建构过程.
1.1 进入“愤”的学习状态
爱因斯坦说,“兴趣是最好的老师”.教师要利用有趣的问题、生动的情境、富有挑战性的场景,让学生主动参与到学习活动中.因此,数学教师要发挥主导作用,精心挑选数学问题、用心设计教学活动,为学生的数学学习搭建广阔的舞台.
教学片断1
师:“鸡兔同笼”是一个古老而有趣的数学问题.它出自我国古代数学名著《孙子算经》.原文是“今有雉兔同笼,上有三十五头,下有九十四足.问雉兔各几何?”
生:它的意思是什么?
生:笼子里有若干只鸡和兔,从上面数有35个头,从下面数有94只脚,鸡和兔各有多少只?
生:这个问题很有意思.如何解答这个问题呢?
师:大家想怎么解决这个问题呢?
生:可以画图,也可以通过一个一个地数去试.
师:你觉得这些方法怎么样?
生:数比较大,画图和试数都很麻烦.
生:那我们把数变小一点,用画图和试数的方法来解决就会简单一些.
师:大家的想法很好.我们现在把数变小一些,问题变成“鸡和兔一共有8个头,26条腿,鸡和兔各有多少只?”大家能解决吗?
在这个教学片段中,教师选择“鸡兔同笼”这个古老而有趣的数学名题,引起了学生极大的学习兴趣.学生们围绕这个富有挑战的数学问题进行思考、交流、讨论,最终发现数太大不好解决,也不容易进行探究,于是化繁为简,即把数变小.由此可见,学生们带着对古代数学题的迷茫和求知欲进入了“愤”的学习状态.
1.2 经历“愤”的学习过程
维果斯基的“最近发展区理论”认为,学生的发展有两种水平:一种是学生的现有水平,指独立活动时所能达到的解决问题的水平;另一种是学生可能的发展水平,即在别人的帮助下能够达到的水平.两者之间的差异就是最近发展区.教学应着眼于学生的最近发展区,为学生提供带有适当难度的内容,调动学生的积极性,发挥其潜能,超越其最近发展区而达到下一发展阶段的水平.学生经历最近发展区的过程,就是努力想要弄明白而又弄不明白的过程,是学生思维苦苦挣扎的过程,也就是“愤”的学习过程.
教学片断2
师:请你用自己喜欢的方法尝试着解决这个简化版的“鸡兔同笼”问题,并把你的想法记录在学习单上.
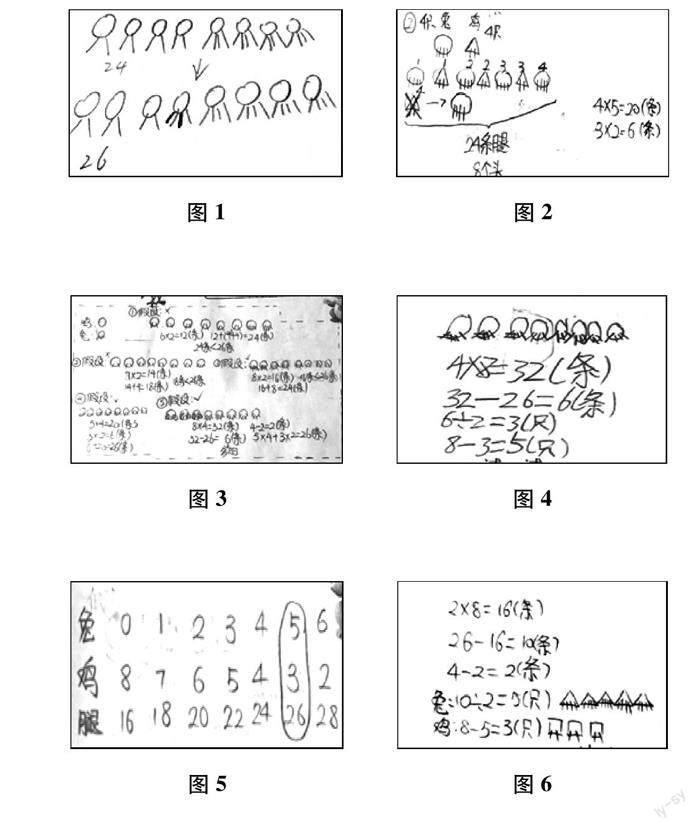
学生自主探究,尝试解决简化版的“鸡兔同笼”问题.教师巡视,根据学生在自主探究过程中出现的问题进行适时的启发和点拨.在巡视过程中教师发现有的学生一直在没有根据地列算式,便会给出提示,“如果列算式有困难,能不能先画画图来表示你的想法?”当学生一直画线段图找不到数量之间的关系时,教师提示,“如果画线段图不好找数量之间的关系,能不能画其它图?”经过一段时间的探索,学生们有了自己的想法(见图1-图6).
在这个教学片段中,教师鼓励学生调动自己以往的学习经验来自主尝试解决问题.在自主探究的过程中,学生经历了思考的困惑,经历了不知所措,也遇到了很多问题.但通过教师的点拨,他们的思维系统被激活,原始经验被调动,进入到了主动探索和合作交流阶段,运用不同的方法解决了问题.教师在学生“愤”的时候,通过“启”来帮学生建立新旧知识间的联系,打开思维的闸门,使学生先“惑”而后“明”.
2 给足表达的机会,让学生走出“悱”的状态
《义务教育数学课程标准(2022版)》提出,通过义务教育阶段的数学学习,学生逐步“会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界”,实现对数学的理解、掌握和运用.学生经历的特殊过程——“用数学的眼光发现和提出问题,用数学的思维与数学的语言分析和解决问题”——其实就是“悱”的过程.
2.1 适时而导,疏通思路
学生对问题的认知是有一个过程的,学生的思路有时会出现“堵塞”.例如,有些学生有思路却难以表达出自己的思考过程;有些学生会找到解决问题的方法却讲不出其中的道理;有些学生越讲越糊涂以致把自己绕进去再也出不来.这就是学生进入“悱”的状态,此时需要教师顺势而导,帮助学生疏通思维通道,走出“悱”的状态.
教学片断3
生:我先画了8只鸡,然后试一试,最后变成了5只兔子3只鸡(见图1).
生:你为什么先画8只鸡?为什么不画8只兔子呢?
學生听后把黑板上的8只鸡改成了8只兔子.
生:你刚才说最后是5只兔子3只鸡.你为什么又把它们画成8只兔子了呢?
学生站在前边一时不知如何回答.教师见女生手足无措,就顺势问:你先画了8只鸡,怎样从这8只鸡想到的5只兔子3只鸡的呢?
生:我发现腿不够.
师:你是怎么知道腿不够的呢?
生:计算.
师:一边画一边计算,是个不错的办法.说说你是怎样计算的?
生:2乘8等于16,16比26少了10条腿.
师:少了10条腿,又该怎么办呢?
这位学生拿起红色粉笔,将这10条腿加上.
师:哪位同学读懂了她的画法?
生:她是给每只鸡加上两2条腿,5只鸡一共加了10条腿,5只鸡变成了5只兔子,还剩3只鸡.
师:你是这样想的吗?你能再完整地说说你的想法吗?
生:我先画了8只鸡,通过计算发现腿少了10条,就给1只鸡加上2条腿,5只鸡一共加了10条腿,最后有5只兔子3只鸡.
在这个教学片断中,同学自己能够解决问题,却难以表达自己的想法,处于懵懂的状态.此时教师适时介入,进行有效的启发引导,帮助学生寻找思维的突破口,排除疑难.学生在教师的引导下,梳理了自己的思路,解决了困惑,走出“悱”的状态.
2.2 适时追问,辨析真理
任何教学中少不了老师和同学的追问.追问是数学课堂教学的重要手段,是精妙的课堂艺术.教师应抓住追问的时机适时追问,使课堂成为智慧启迪、心灵碰撞的场所.当学生的思考出现错误、矛盾、困惑时,教师应及时追问,激活学生思维,促进学生深入思考.学生在追问中慢慢地“悟”,在交流思辨中理清知识的来龙去脉.
教学片断4
在全班交流环节,还有一位男同学用列算式的方法解决了问题(见图5).
生:我是这样想的:8乘2等于16条,26减16等于10条,10除以2等于5只,兔子5只,8减5等于3只,鸡有3只.大家还有什么疑问?
师:咱们来问问他,8×2=16(条)表示的是什么?
生:就是先把这8个头假设成8只鸡,8乘2等于16,一共有16条腿.
生:为什么26-16=10(条)?
生:26-16=10,就是差10条腿.
生:那10÷2=5是什么意思?
生:还差10条腿,每只鸡是2条腿,10除以2等于5.
生:这个“2”是鸡的腿吗?
教师见学生面露疑惑,于是追问道,“谁能说说这个‘2表示的是什么?”
生:我们可以结合刚才的图来帮助理解,这个“2”不是鸡的腿,是给每只鸡添上的2条腿,添了5个2,所以是10÷2=5(只).
师:这5只是鸡还是兔呢?
生:是兔,因为每只鸡添上2条腿后就变成了兔,10除以2等于5,添了5个2,相当于把5只鸡变成了兔,所以5是兔的只数.
师:你明白了吗?这个2是什么?
生:是给每只鸡添上的2条腿.
师:为什么是添上2条腿呢?
生:因为鸡添上2条腿才能变成兔.
师:“2”是怎样求出来呢?
生:4-2=2(条).
师:10÷2=5(只)表示的是什么?
生:还差10条腿,每只鸡添上2条腿后就变成了兔,10除以2等于5,也就是添上了5个2,把5只鸡变成了兔.
在这个教學片断中,同学虽然可以自己列式解决问题,但只能读出每一步算式,讲不明白其中的道理.教师引导学生追问,“8×2=16(条)表示的是什么?”,并给予点拨和启发.在学生“悱”的时候,教师“发”,其他学生“顺藤摸瓜”,摸清了提问的方法.在交流对话中,学生的思路一步一步变得清晰.接着,师生抓住本课难点进行追问——“10÷2=5是什么意思?”学生回答:“还差10条腿,每只鸡是2条腿,10除以2等于5.”这样,又一次引发了认知的冲突——“这个2到底是什么呢?”.随着生生对话的深入,结合图形直观,学生终于弄清了“2”表示的意义,攻克了“鸡兔同笼”问题的难点.
总之,基于启发式教育思想,在教学过程中,教师要把学生当作学习的主人.教师应最大限度地把课堂交给学生,让他们充分经历知识的形成过程.教师应该给予学生足够的思考空间,让其在“愤”中学会思考.此外,教师还需要给予学生足够的表达机会,让其在“悱”后学会表达.在小学数学教学中,只有让学生的数学思考真正发生,数学核心素养才会落地生根.
参考文献:
[1] 中华人民共和国教育部.义务教育数学课程标准[S].北京:北京师范大学出版社,2022.
[2] 张爱华,钱铭.不愤不启,不悱不发——两节同课异构的新授课对比反思[J].数学学习与研究,2017(5):166-167.
[3] 苏静霞,马绍文.基于“综合与实践”活动培养学生发现和提出问题的能力[J].数学之友,2022,36(1):16-18+21.
[4] 刘艳鲜.利用Geogebra开展线性规划问题探究例析[J].数学之友,2022,36(1):77-79.
[5] 王思俭.基于单元教学情景的新概念课堂教学设计与研究——以《导数在研究函数中的应用》为例[J].数学之友,2022,36(2):14-18.
[6] 樊欣,马小琼,韦华益,唐剑岚.动感技术的融合提质增效数学教学——以“反比例函数图象与性质”教学片段为例[J].数学之友,2022,36(2):88-89+93.

