HPM视角下二项式定理的教学设计
金正娇 刘熙

摘 要:HPM视角下的教学是当今教育的一大革新.“二项式定理”蕴含着浓厚的数学文化底蕴,其发展源远流长.本文追溯二项式定理的发展历程,并对其进行重构式教学运用.首先,以法国数学家蒙特摩尔的筹码游戏为切入点,猜想二项式定理,感受数学的探究之乐;其次,采用“组合数分析法”和意大利数学家卡斯蒂隆的“先异后同法”证明二项式定理,帮助学生形成数学理性思维;再次,借助杨辉三角探究二项式系数的性质,既加强数与形的结合,又传承中华优秀传统文化;最后,设计具有综合性、探究性、启发性的课后作业,深化基础知识,启迪数学思考.
关键词:HPM;二项式定理;中华优秀传统文化;教学设计
1 教材分析
“二项式定理”选自人教A版选择性必修第三册第六章第三节,解决二项n次式的展开问题,与初中代数知识密切联系,是继高中排列与组合之后的学习内容.在牛顿发明微积分的过程中,二项式定理的发现是一个关键节点[1],二项式定理也是连接初等数学与高等数学的一座桥梁,因而二项式定理贯穿了初中—高中—大学阶段.
2 学情分析
学生在初中阶段已经掌握了多项式的乘法法则,在高中阶段的同章前两节已经学习了分步乘法计数原理和组合数的相关知识,具备从组合的视角思考问题和分析问题的能力;已经学习了数学归纳法,具备一定的抽象概括和归纳能力.
3 教学目标
① 掌握二项式定理、二项展开式的通项公式,会求二项式特定的项和系数,会应用二项式系数的基本性质;
② 从二项式定理的历史轨迹出发,引导学生得出二项式定理,归纳二项式系数的基本性质,体会归纳—猜想—论证的思想方法,培养学生的探究能力和邏辑思维能力;
③ 从二项式定理的相关历史出发,培养学生的数学文化素养和严谨求实、坚持不懈的探究精神.
4 教学重难点
教学重点:二项式定理的得出、二项式系数的性质总结.
教学难点:二项式定理的推导、二项式系数与组合知识的联系.
5 教学过程
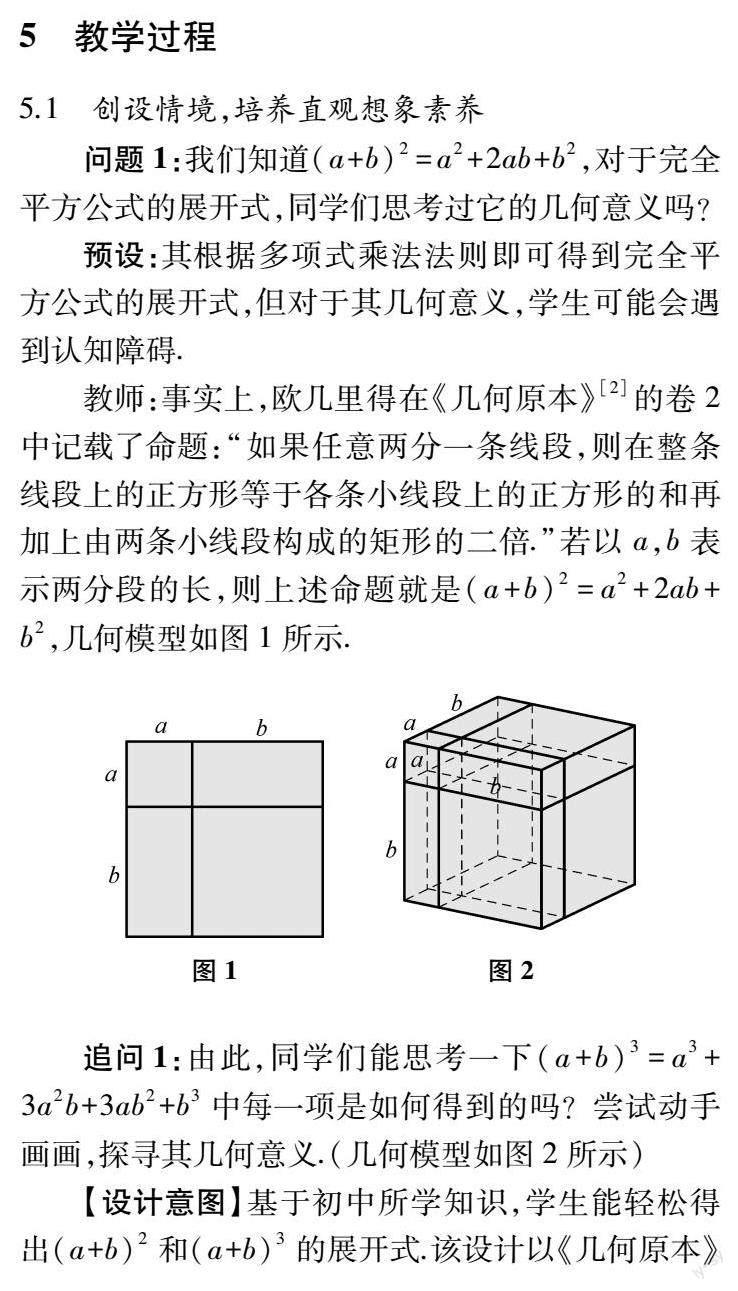
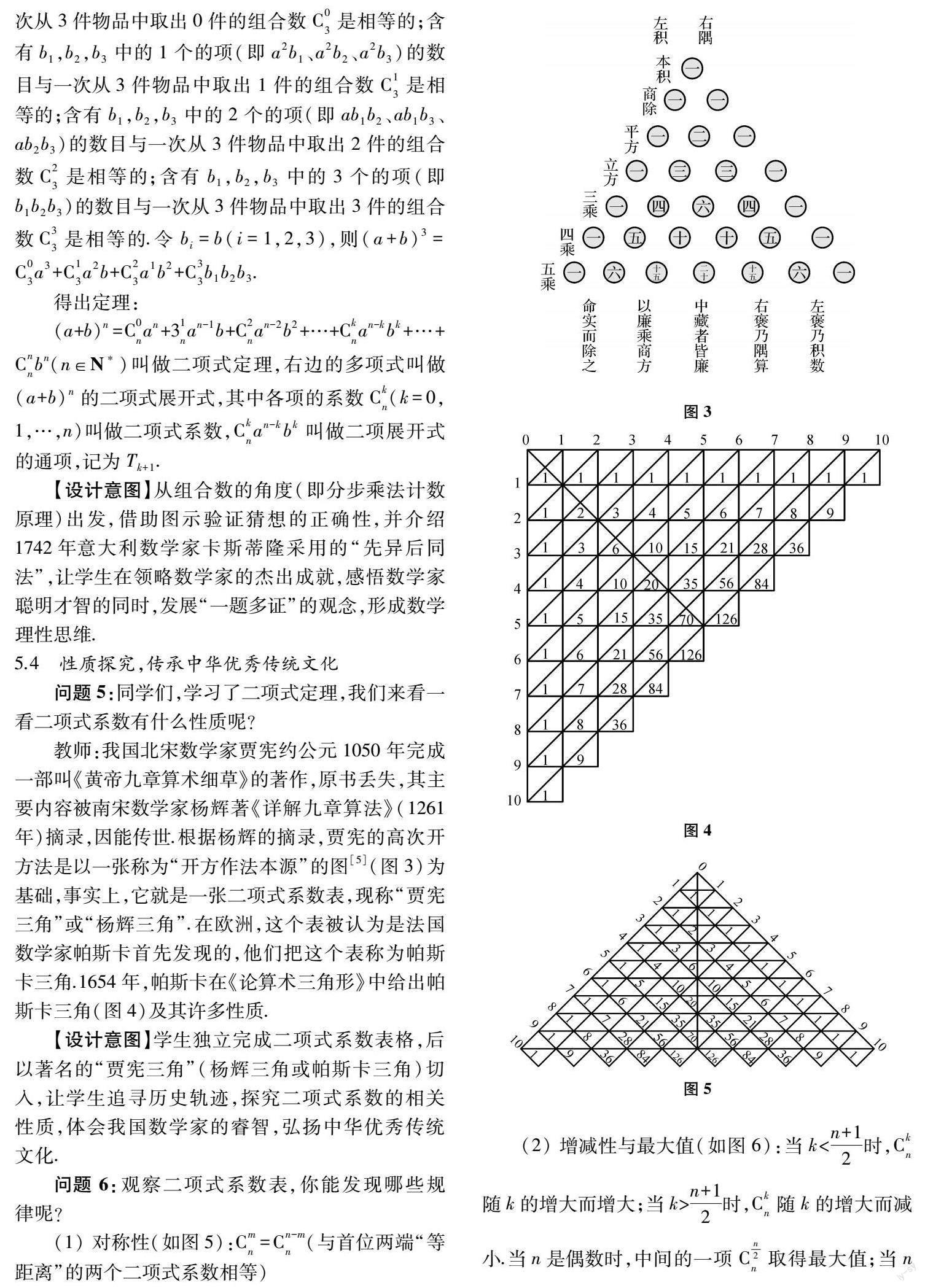
5.1 创设情境,培养直观想象素养
【设计意图】在历史上,德国数学家莱布尼茨和瑞士数学家约翰·伯努利将正整数次幂的二项式定理推广到三项以上情形,实现了二项式定理的多元推广,实现了定理的“横向”推广,即“元”的推广.以历史定理进行设问,培养学生的推理论证和逻辑思维能力,继续探究多元多项式的展开,让学生领略古人的杰出成就,感受数学文化,实现知识层面的进一步飞跃,提高发现和提出问题的能力、分析和解决问题的能力[6].
参考文献:
[1] 宋军,吴现荣.源于数学史,教学更自然——二项式定理教学设计[J].福建中学数学,2017(11):1417.
[2] 欧几里得.几何原本[M].兰纪正,朱恩宽,译.西安:陕西科学技术出版社,2003.
[3] 汪晓勤,韩祥临.中学数学中的数学史[M].北京:科学出版社,2002.
[4] 李文林.数学史概论(第二版)[M].北京:高等教育出版社,2002.
[5] 人民教育出版社课程教材研究所,中学数学课程教材研究开发中心.普通高中数学教科书选择性必修第三册[M].北京:人民教育出版社,2020.
[6] 中华人民共和国教育部.普通高中数学课程标准(2017年版2020年修订)[M].北京:人民教育出版社,2020.

