以数线促进估算的理解
王小莲
【摘 要】数线,即表征数的意义、性质和运算的线,是一种教学辅助工具。求小数近似数的难点在于四舍五入,它从整数的区间数判断走向了较为抽象的小数区间数判断。教学中,教师创造性地利用数线表征数的意义,用多维视角理解估算,用数形结合的方法促进学生对小数估算的理解,发展学生的数感,也为学生后续建立整数、分数、小数等不同数系之间的联系积累活动经验。
【关键词】小数近似数;数线;估算;表征
【课前思考】
数线,即表征数的意义、性质和运算的线,是一种教学辅助工具。利用数线估计是解决日常生活中常见问题的一种数学能力,能帮助学生理解相应的知识内容。近似数和估算教学的关键有两点:一是从确切的数扩充到表示范围的区间;二是根据实际情况确定范围。[1]人教版教材四年级下册在编排“小数的近似数”这一内容时,以“求小欣身高的近似数”这一现实问题引入,接着出示“求一个小数的近似数,同求整数的近似数相似”这一迁移性结论,并直接给出四舍五入求近似数“看尾数首位,即省略的尾数部分最高位上的数”[2]的方法性结论。这样的编排方式重视方法的指导,却忽视了原理的理解。因此,学生在学习时易出现以下难点:一是为什么保留两位小数,要看千分位;二是在表示近似数时,小数末尾的0为什么不能去掉。
基于上述问题,笔者进行了整数近似数的调研。调研发现,学生虽然能正确解答,却说不清楚“四舍五入到万位要看千位”的道理。这一现象暴露出学生对整数近似数的理解并不深刻。“为什么可以用四舍五入法求小数的近似数?保留一位小数,为什么只要看百分位就可以了?在表示近似数时,小数末尾的0为什么不能去掉?”[3]在针对五年级学生(学习过小数的近似数)的访谈中,学生对这些问题一脸茫然。由此可见,学生在近似数原理的自然迁移上具有一定困难。
那么,如何才能让学生更好地理解近似数,并能运用近似数解决问题呢?针对这一教学难点,教师可创造性地运用具象的数线,化抽象为形象,引导学生通过数线观察,将整数的四舍五入近似法则迁移到小数中;通过数线对比,解决“看尾数首位”这一关键难点,深刻理解“四舍五入”求小数近似数的方法;通过数线推理,深刻理解精确度,体会近似数背后的区间思想,发展学生的测量和数感等数学能力。
【教学目标】
1.能够根据要求用“四舍五入法”保留一定的小数位数,求出小数的近似数。
2.在对数线模型的探索中归纳求小数近似数的方法,体会近似背后的区间思想,理解在表示近似数时小数末尾的0不能去掉的本质。
【教学重难点】
借助直观数线,掌握用“四舍五入法”求小数近似数的方法。理解保留的位数不同,求得近似数的精确度也不一样。
【教学过程】
一、观察数线,理解为什么要和中间数进行比较
1.经验回溯:求整百数近似数的方法
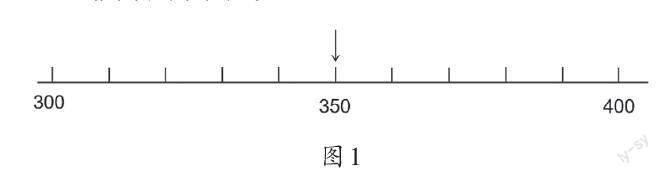
教师出示图1。
师:在图1这条数线中,哪些数接近300?哪些数接近400?你是怎么想的?
生:30?、31?、32?、33?、34?这些数接近300;35?、36?、37?、38?、39?更接近400;350正好在中间。
生:十位比5小就接近300,十位比5大就接近400。
师:原来,我们只要看十位就能知道这个数是离300近还是400近。
2.方法回溯:求整十数近似数的方法
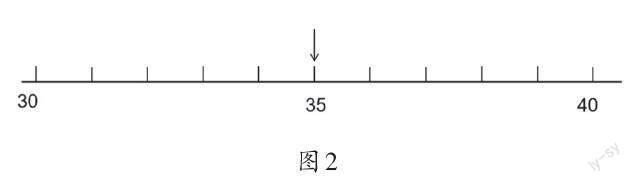
教师出示图2。
师:在图2这条数线中,哪些数接近30?哪些数接近40?你是怎么想的?
生:个位比5小就接近30,个位比5大就接近40。
生:只要把这个数和35进行比较就可以了。
师:请大家观察这两条数线,判断数字的近似数时,是和谁进行比较?
生:只要和中间的数35或350进行比较,就能快速判断它的近似数。
师:我们在求一个数的近似数时,都是把这个数和中间的数进行比较,这个方法就是“四舍五入法”,而且中间的数也是要“五入”的。
评析:求小数的近似数和求整数近似数的方法相近,都是用“四舍五入法”。但随着数域的扩大,学生在小数范围内应用“四舍五入法”有一定难度。与教材直接给出迁移性结论相比,上述环节的设计能为将“四舍五入法”从整数迁移到小数提供直观支持。它承接了整数范围内求近似数的经验,利用观察数线的活动,探究“哪些数更接近”“判断近似数时是和谁进行比较”的关键问题,从而连接“舍”“入”和“远”“近”。学生通过数线上中间数的分段,感知求一个三位数的近似数要关注十位,求一个两位数的近似数要关注个位。以求整百数近似数的方法为例,十位是0~4对应“四舍”,十位是5~9对应“五入”,直观形象地对“四舍五入法”进行了迁移。
二、对比数线,理解“为什么要看尾数首位”
1.保留到整数,为什么只看十分位
师:老师的身高是1.69米,保留整数是多少?
生:1.69比1大,比2小,保留整數可能是1或2。
生:1.69离1远,离2近,所以1.69保留整数是2。
教师出示图3,图中的数线将1和2之间的线平均分成了10份。
师:观察图3中的数线,我们在判断1.69离谁近时其实是将它和谁进行比较?
生:我是把它和1.5进行比较。比1.5大就接近2,比1.5小就接近1。1.69在1.5的右边,更接近于2。
师:比较1.69和1.5时,整数部分都一样,关键是比较什么?
生:保留整数时,1.69和1.5的整数部分都一样,只要将十分位上的6和5进行比较即可。6比5大,所以1.69约等于2。
生:我还发现在精确到个位时,不用看百分位和千分位,只要将十分位进行四舍五入就可以了。
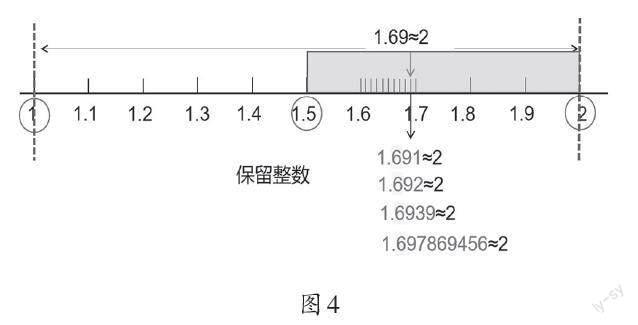
教师用课件动态演示图4,并追问。
师:那1.691保留整数呢?1.692呢?1.6939呢?1.697869456呢?你有什么发现?
生:只要十分位上的数比5大,精确到个位都是2。
师:到底是哪个数位上的数决定了保留整数都约等于2?
生:是由十分位上的6决定的。
师:只要十分位上的数比5大,不管后面数位上的数是几,对最后的结果都没有影响,在保留整数时都约等于2。所以,保留整数只需看十分位。
2.保留一位小数,自主探索求近似数的方法
师:那将1.69米保留一位小数会是多少?把你的探究过程记录在数线上。
学生独立思考,并将探究过程记录在作业纸的数线上。
生:我是将1.6和1.7之间的格子再平均分成10份,找到1.69,发现1.69在1.6和1.7之间,离1.6远,离1.7近,所以1.69保留一位小数是1.7(如图5)。
生:我是把它和1.6与1.7中间的1.65进行比较,比1.65大就接近1.7,比1.65小就接近1.6。
师:你们在比较1.69和1.65时,关键是在比较什么?
生:保留一位小数时,关键要比较百分位上的9,9比5大,所以1.69约等于1.7。
师:那1.691保留一位小数呢?1.692呢?1.6939呢?1.697869456呢?观察这些数据,到底是哪个数位上的数决定了它们在保留一位小数时都约等于1.7呢?
生:这些数的百分位都是9,其实只要百分位上的数大于或等于5,不管千分位、万分位上的数是几,这些数在保留一位小数时都约等于1.7。
师:所以在保留一位小数时,只需要将百分位四舍五入就可以了。
3.保留两位小数,迁移应用求近似数的方法
师:通过精准测量,老师的身高是1.697米,现在不看数线图,根据刚才的经验,你知道怎么保留两位小数吗?
生:1.697保留两位小数在1.69和1.70之间,千分位是7,离1.70更近,所以1.697保留两位小数约等于1.70。
生:保留整数要看十分位,保留一位小数要看百分位,那么保留两位小数就要看千分位。将千分位四舍五入,7大于5,所以1.697约等于1.70。
师:看来,求整数近似数的方法在求小数近似数时同样适用,都需要用“四舍五入法”保留一定的小数位数。
评析:教师将数线不断均分,以具体的形助力学生对抽象的数区间的理解,引导学生明白将一个小数保留到整数只要和十分位上的5进行比较,再利用“四舍五入法”进行判断即可。教师先提供多组数据,不断向学生追问,让学生理解不管是三位小数还是更多位数的小数,将它们保留一位小数只需看百分位上的数。接着利用学生第一次的比较经验,开展保留一位小数和两位小数的说理探究,让学生在数线的“远近模型”中形成求近似数要看尾数首位的推理判断经验,用数线感悟小数区间数范围,完善对保留小数位数的原理的探究。
三、利用数线,理解“小数末尾的0为什么不能去掉”
1.借助数线表征,寻找近似区间
师:刚才将1.697米保留两位小数时,出现了两种答案:1.7米和1.70米。你们同意哪种答案?为什么?
生:我认为都对,1.7和1.70都表示1米7分米,答案是一样的。
生:我认为不对,因为1.7是一位小数,而我们需要保留两位小数。
师:大家有不同的意见,那到底哪种说法对呢?请你在数线上找一找、画一画,并把你的想法和同桌进行交流。
学生先在作业纸(如图6)上独立完成,再和同桌交流。
生:一个数保留一位小数后是1.7,所以关键要看百分位。百分位上可能是1、2、3、4,那么这个小数可能是1.7到1.74之间的数。
师:在1.7的右边,你找到了4个近似数是1.7的两位小數。那么在1.7的左边有这样的数吗?
生:在1.7的左边还有1.69、1.68、1.67、1.66、1.65。
师:利用将百分位四舍五入的方法,你们在数线上找到了近似数是1.7的两位小数,那么这个数有可能是三位小数吗?
生:它还可能是1.701、1.712、1.734、1.748……
师:为什么这些小数保留一位小数也是1.7?这样的数还有多少个?我们一起把这些数的范围画出来。
教师用课件动态演示图7。
生:近似数是1.70,说明是要把这个数保留两位小数,所以要看千分位上的数。我在数线上找到了1.695、1.696、1.697、1.698、1.699、1.700、1.701、1.702、1.703、1.704这些三位小数。
生:除了这些三位小数,只要大于等于1.695,小于1.705,不管是几位小数,它保留两位小数的近似数都是1.70。
教师用课件动态演示图8。
2.合并表征结果,对比精确区间
教师用课件动态演示,合并图7、图8,得到图9。
师:刚才我们通过数线的推理,找到了近似数是1.7和1.70的小数范围,仔细观察,它们一样吗?
生:1.70的近似范围要比1.7的近似范围小得多,它们是不一样的。
师:想象数线,1.700的近似范围在哪里?1.7000的呢?你有什么发现?
评析:教师借助数线帮助学生建立起“小数末尾的0代表这个近似数的精确程度”的直观模型,紧扣“一个数的计数单位越小,它的精确程度就越高”的意义本质。在准确数和近似数的比较中,数概念的学习从一个确定的数扩展到一个区间,这也是数感的表现之一。一个小数的近似数同样和计数单位有关,一个数的计数单位越小,它的精确度就越高。[4]通过数线中精确区间的直观呈现,学生理解了去掉小数末尾的0会直接影响数的精确度和对应区间数。
【教学反思】
一、从数线感悟小数区间数的范围,完善对保留小数位数的原理探究
四舍五入求近似数“看尾数首位”的结论性方法对学生来说难度很大。教学中,教师除了要利用整数“四舍五入法”进行自然迁移,还要引导学生探究为什么保留一位小数就要把百分位上和后面的数都省略,即“为什么只要看百分位”“小数尾数为什么可以去掉”等问题。教学时,教师借助数线,化抽象为具体,紧扣核心概念“计数单位”,促进学生对小数意义的理解,通过学生熟悉的活动,引导学生直观看到小数最接近的数,利用小数区间范围的数理解“看尾数首位,即省略的尾数部分最高位上的数”进行四舍五入的原因,完善对小数位数原理的探究。
二、从数线感知数与距离的关系,完善对小数意义教学的整体建构
精确数是一个点,而近似数是靠近精确数的一段范围内所有点的集合。教师可引导学生利用数学的均分特征,找到相应小数所在位置与起点和终点的距离,在数线的“远近模型”中,形成求近似数要看尾数首位的推理判断能力,积累经验,更加深入形象地理解小数的意义;在利用数线和创作数线的过程中建构模型,促进数线的产生,感受计数单位的细分,从而完善对小数意义的整体建构。
参考文献:
[1]章勤琼. 3.8是3.80的近似数吗:近似和估算教学的关键是什么[J]. 教学月刊·小学版(数学),2019(4):60-63.
[2]朱绍敏.数形结合 直观感悟:数线解决四舍五入求近似数看尾数首位问题[J].小学教学设计,2017(11):25-26.
[3]张雅芬.巧借数轴 探其本质:“求小数的近似数”片段赏析[J].数学学习与研究,2015(19):87,89.
[4]吴正宪,张秋爽.整体把握教材 突出数概念本质:“小数的意义和性质”单元教学思考[J].小学教学(数学版),2020(5):25-27.
(浙江省温州市龙湾区教师发展中心)

