基于测地轮廓和特征函数的灰度异质图像分割
徐思敏,金正猛,闵莉花,王 皓,郭小亚
(南京邮电大学 理学院,江苏 南京 210023)
0 引 言
图像分割是根据某种均匀性或一致性原则把图像分成具有特定性质区域的过程,是图像处理和计算机视觉领域的基本任务之一,在机器视觉、医学成像、自动驾驶、对象检测和交通控制系统等领域有广泛应用。在自然或医学图像成像过程中,由于光照或设备偏移场的影响,图像会出现灰度异质问题,从而严重影响图像分割的精度。该文主要关注针对灰度异质图像的分割方法。
近年来,活动轮廓图像分割模型备受关注。现有的活动轮廓模型可分为:基于边缘的分割模型和基于区域的分割模型。基于边缘的分割模型主要依赖图像的边缘信息捕捉目标物体的边界,如:著名的Snake模型[1]和测地活动轮廓模型(Geodesic Active Contour,GAC)[2]等。基于区域的分割方法,主要利用图像中物体呈分片区域的特点来引导初始轮廓的演化,如:经典的Mumford-Shan(MS)模型[3]。由于MS模型的求解过于复杂,Chan等人[4]将不同区域的灰度值近似为分片常数,并用水平集函数[5]来表示轮廓线,提出经典的Chan-Vese(CV)模型。近年来,为了提高边缘处的分割精度,Bresson等人[6]将GAC模型中的测地轮廓长度项引入CV模型中,提出基于测地轮廓的CV分割模型(简称g-CV模型),该模型能更好地捕捉边缘信息,提高对目标物体的分割精度。由于CV和g-CV模型都是在图像灰度均匀的前提下建立的,对分割灰度异质图像,其分割精度难以得到保证。
为了有效分割灰度异质图像,Zosso等人[7]根据Retinex理论[8-9]将图像分解为光照部分和反射部分之和,提出CVB模型用于图像分割和偏移场矫正。该模型能较好分割灰度异质图像,但仍然存在以下问题:一方面,CVB模型没有整合目标物体边缘信息,容易出现过度分割或欠分割问题。另一方面,文献[7]使用结合交替极小化[10]和阈值动力学[11-12]的算法求解CVB模型,计算过程中需要求解复杂轮廓演化的偏微分方程,求解速度并不可观。
为了提高CVB模型的分割精度,该文在CVB模型的基础上引入测地轮廓长度项,提出新的变分分割模型(简称g-CVB模型)。此外,受轮廓长度近似公式[13]的启发,该文提出用特征函数表示测地轮廓长度项,并结合交替极小化算法和迭代卷积阈值法设计新模型的求解算法。该算法的优势体现在:(1)可以通过简单的迭代卷积阈值法进行交替求解,计算效率高。(2)在交替求解过程中,每个子问题的求解都是稳定的。最后,实验结果表明:该算法不仅能有效分割灰度异质图像,其收敛速度还有明显提升。
1 相关工作
文中,Ω⊂R2表示具有Lipschitz边界的有界图像域,I:x∈Ω为输入图像,Γ为封闭边界曲线,*表示卷积运算符,∇表示梯度算子。
1.1 基于特征函数的GAC模型
传统GAC模型使用水平集表示能量泛函,在求解时存在计算效率低和数值不稳定的问题。为了解决上述问题,Ma等人[13]使用特征函数表示能量泛函,结合迭代卷积阈值法(Iterative Convolution Threshold Method,ICTM)求解模型,其方法概括如下。定义特征函数u(x):
(1)
其中,Γ表示待分割对象的边界,ΩΓ表示Γ内部的区域。根据文献[14],目标的测地线长度近似表示为:
(2)
其中:τ>0,边缘检测函数为:
(3)
其中,γ为大于0的参数,Gτ和Gσ均为高斯核函数。
由测地线长度项结合面积项得到基于特征函数的GAC模型的能量泛函近似为:
文献[13]中Ma等人基于上式使用迭代卷积阈值法进行求解,相较于传统水平集方法,该算法求解速度更快,收敛更稳定。
1.2 CVB模型
2017年,Zosso等人[7]将Retinex理论应用到CV图像分割模型中,提出CVB模型。该模型不仅能有效分割灰度异质图像,且能较好地对输入图像进行偏置矫正。
设i(x,y)是灰度异质图像,Retinex理论将其分解为光照部分b(x,y)和反射部分s(x,y)的乘积:i(x,y)=b(x,y)·s(x,y),两边同时进行对数变换得:
logi(x,y)=logb(x,y)+logs(x,y)
(4)
令I=log(i),B=log(b),S=log(s),则式(4)可以简化为:
I=B+S
(5)
其中,B被认为是光滑函数,表示图像中光照偏移场部分,S被认为是分片常数函数,表示反射部分。假设输入函数I满足式(5),得到如下分割灰度异质图像的CVB模型:
其中,λ1,λ2,α,β>0为参数。使用水平集函数φ的零水平来表示Γ,引入Heaviside函数[5]H(φ),令u:=H(φ)且凸松弛为u:Ω→[0,1],得到下式:
s.t.I=B+S
模型第一项是偏移场B的平滑项,第二、三项是数据保真项,最后一项是长度正则项。
在文献[7]中,Zosso等人结合交替极小化和阈值动力学算法来求解CVB模型,并结合相场方法[11]和MBO方案[12]设计基于阈值动力学的算法来求解关于u的子问题,但因为该算法需要求解复杂的轮廓演化的偏微分方程,求解速度较慢。此外,上述CVB模型中的长度正则项是以分割结果的长度项最小为目标,在分割尖锐边界时容易出现欠分割问题。
2 文中模型及算法
2.1 文中模型与算法
为了充分利用图像边缘信息,该文利用GAC模型中的测地长度项取代CVB模型中原有的长度项,提出如下的g-CVB模型:

s.t.I=B+S
(6)
用式(1)中的特征函数u(x)隐式表示Γ,可将g-CVB模型转化为:
s.t.I=B+S
(7)
其中,τ、λ1、λ2、α为正参数,M:={u∈BV(Ω,R)|u={0,1} },BV(Ω,R)为有界变差函数空间[15]。
结合交替极小化和迭代卷积阈值法,该文设计一种高效的数值求解算法。将式(7)转换为无约束极值问题,其对应的增广拉格朗日函数为:
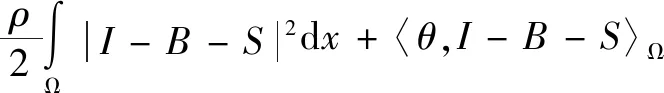
(8)
其中,ρ是罚参数,θ是拉格朗日乘子。首先固定c1,c2:
接下来,分别对各子问题进行求解:
(1)求解关于u的子问题。

这里记:
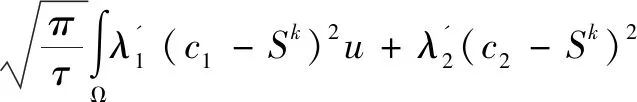

(10)
注意到能量泛函最小化问题式(10)的可行集M是非凸的,直接求解式(10)是困难的,因此将M松弛到它的凸包K:= {u∈BV(Ω,R)|u∈[0,1] }上,得到问题式(10)松弛后的极小化问题:
(11)
该文在2.2节中给出求解式(10)与式(11)的等价性证明。
接下来,通过迭代卷积阈值法来求解关于u的问题式(11)。很容易证明,Eτ(u)是一个凹泛函,而凹泛函的图像总是低于它的线性逼近,故可将求Eτ(u)的最小值问题近似等价于求Eτ(u)的线性逼近的最小值问题[17]。具体来说,计算Eτ(u)在第k次迭代uk处的一阶泰勒展开式:
其中:

继而,通过求解下列线性化问题得到k+1次迭代uk+1:
对于∀x∈Ω,可解出:
由于凸集上的线性泛函的最小值必在边界处达到,因此:
(2)求解关于B的子问题。
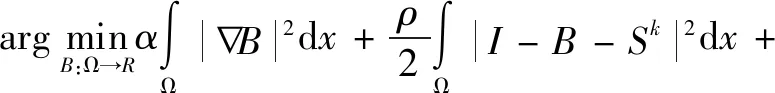
〈θk,I-B-Sk〉Ω
其对应的欧拉-拉格朗日方程为:
ρBk+1-2αΔβk+1=θk+ρ(I-Sk)
通过快速傅里叶变换,求解得:
(3)求解关于S的子问题。

|I-Bk+1-S|2dx+〈θk,I-Bk+1-S〉Ω
解得:
其中:
Q1=2[λ1uk+1c1+λ2(1-uk+1)c2]+
ρ(I-Bk+1)+θk
Q2=2[λ1uk+1+λ2(1-uk+1)]+ρ
(4)更新θ。
θk+1=θk+ρ(I-Bk+1-Sk+1)
依次迭代上述求解过程直到满足收敛条件。具体流程如算法1所示。
2.2 等价性证明
下面的引理1证明了求解式(10)与式(11)的等价性。
引理1:求解原问题式(10)与求解其松弛后的问题式(11)是等价的,即若u*是式(10)的解,则它同样是式(11)的解,反之亦然。


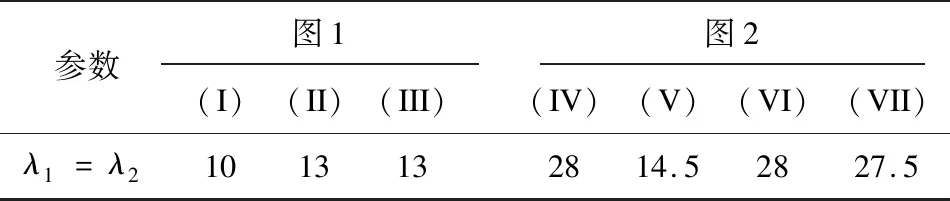
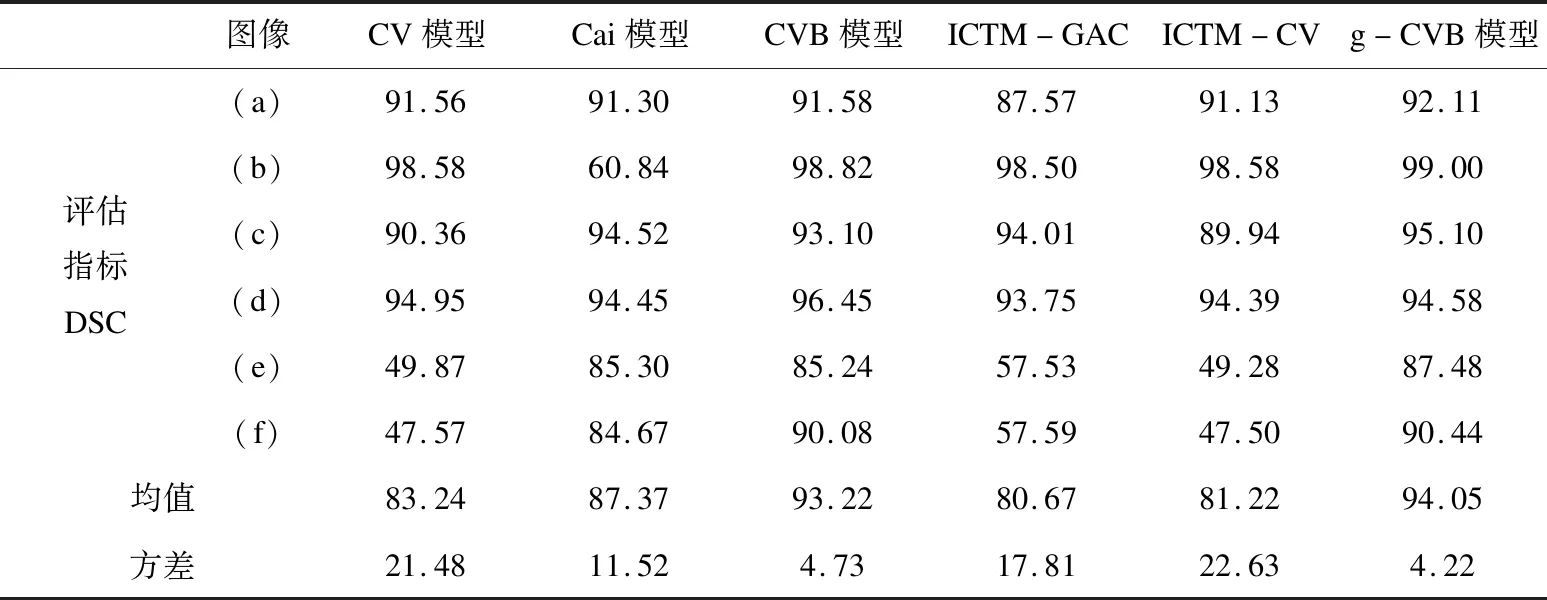
对于|t| 二阶导为: 算法1:文中算法的求解流程。 1.初始赋值:S0=I,B0=(0,0),θ0=0,u0取决于初始轮廓. 2.迭代:更新uk+1,Bk+1,Sk+1如下: 在本节中,定理1证明了对于任意的τ>0,Eτ(u)在迭代过程中逐渐减小。即算法1是无条件稳定的。 定理1 令uk(k=0,1,2,…)为算法1中u的第k次迭代,对任意τ>0,有Eτ(uk+1)≤Eτ(uk)。 证明:对式(9)做线性化处理可得: 将uk带入Eτ(u)得到: 进一步, 因为uk+1是序列线性规划的一个解,故: Lτ(uk+1,uk)≤Lτ(uk,uk) 进而: Eτ(uk+1)-Eτ(uk)=Lτ(uk+1,uk)-Lτ(uk,uk)+ζ其中: 可得: 因此Eτ(uk+1)-Eτ(uk)≤0。证毕。 本节中,对多幅不同类型的灰度异质的图像进行分割,并同CV模型[4]、Cai模型[18]、CVB模型[7]、ICTM-GAC算法[13]以及ICTM-CV算法[19]的分割结果进行对比,以检验文中方法的有效性。为了定量地评价不同方法的分割性能,这里采用Dice相似系数(Dice Similarity Coefficient,DSC)[20]和Hausdorff距离(Hausdorff Distance,HD)[21]作为评价指标。它们的定义分别是: (12) HD(A,B):= (13) 其中,S1代表分割后目标物体的区域,S2代表对应的真实区域,A为分割后的二值图像,B是相应的真实二值图像,n表示分割目标边界集的总数。DSC值越高,HD值越低,表示分割结果越精确。在提出的模型(7)中,设置参数τ=0.4,λ1=λ2,平滑参数α=9 000,不同图像对应的λ1、λ2的值列于表1中。在算法1中固定惩罚参数ρ=92,设置停止准则tol=10-5。 表1 参数λ1、λ2的取值 首先,图1展示了不同模型与算法对三幅合成图像的分割结果。其中,第一列为带有初始轮廓(白色线)的合成图像,后面依次是CV模型、Cai模型、CVB模型、ICTM-GAC算法、ICTM-CV算法和文中算法的分割结果。从图中可以看出,输入图像中的偏移场严重影响了CV模型和Cai模型的分割性能,这两种模型都未能对目标进行整体分割。CVB模型在分割灰度异质图像时,能对输入图像进行偏移场矫正,但不能分割出一些尖角边缘。ICTM-GAC算法分割效果不佳,ICTM-CV算法受偏移场影响分割出错误边缘,然而文中算法能精确地分割出尖角边缘,得到最优的分割结果。进一步,观察表2中各个模型分割结果的DSC、HD值,发现文中算法有较高的DSC值与较低的HD值,分割结果较好。 图1 不同算法对合成图像的分割结果 表2 图1中分割结果的DSC、HD值、迭代收敛步数及收敛时间 其次,对加有不同偏移场的灰度异质MR图像中的脑白质进行分割,实验结果如图2所示。可以发现,文中算法能准确识别细微的脑灰质得到更精确的分割结果。进一步,通过表3的数据进行定量分析,文中算法取得的DSC和HD值要优于其他算法,且其收敛速度更快。 图2 不同算法对MR脑图像白质的分割结果 表3 图2中分割结果的DSC、HD值、迭代收敛步数及收敛时间 为验证文中方法对原始图像分割的有效性,图3给出了文中方法对来自魏茨曼分割数据集[22]上的8幅灰度异质原始自然图像的分割结果,并与其他方法作对比。文中方法能精准分割出目标物体边缘且在一些细节边缘表现较好。表4给出了各算法对6幅原始图像分割结果的DSC值,文中算法的DSC均值最大,且方差较小,稳定性较强。可以说明,文中算法对原始图像分割精度较高。 图3 不同算法对原始图像的分割结果 表4 图3中分割结果的DSC值 % 在CVB模型的基础上,提出基于测地轮廓长度和特征函数的灰度异质图像分割方法。通过对灰度异质的合成图像、MR图像和原始图像进行分割,结果表明该方法分割精度较高,且收敛速度明显提升。


2.3 稳定性分析


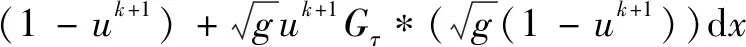

3 实验结果及分析
3.1 合成图像与MR图像的数值实验结果




3.2 原始图像数值实验结果

4 结束语

