基于图割和局部算子的图子集选取

陈丹冉,王 健

(复旦大学 大数据学院,上海 200433)

0 引 言

在统计学、信号处理、计算机视觉等学科中传统关注的数据多为结构化的,如音频、雷达信号、生物医学信号、图像和视频等。随着信息技术的高速发展,当今社会万物互联,数据来源分散且多存在于不规则拓扑结构,如社交网络[1]、传感器网络[2]、生物网络[3]等。这些网络结构数据,大多存在与节点相关的特征,如社交网络中用户的年龄等属性,传感器网络中的各个传感器的观测值,这些节点数据可以视作一种图上的信号。对于分布式的网络信号,传统的信号处理理论无法很好地描述其节点之间的相互关系,因此,图信号处理(Graph Signal Processing,GSP)应运而生,通过引入图上的傅里叶变换(Graph Fourier Transform,GFT),将时间信号推广至基于图网络表征非规则域中的信号。

图网络的拓扑结构复杂多变,同时,较高的数据维度会使得计算复杂度增加,故在资源有限的情况下,能够直接观测到的图信号个数变得十分有限。如何利用少部分最具有信息量的节点的观测值与图结构信息去准确快速地估计未观测的节点信号,进而为图结构数据的传输处理提供高效的技术支撑,是图信号处理中的核心问题,即图信号采样与重构。该问题依赖于一个隐含假设——信号的平滑性,即图上邻近的节点具有相似的值。通常,图信号处理中的平滑性假设采用图傅里叶基的(近似)带宽限制(Band-limitedness)形式,从而使得原始信号能够被部分采样信号重构。

目前,对图信号采样与重构的研究大致可分为局部观测[4-5]与图子集选取(Graph Subset Selection,GSS)[1,6-14]两类。前者利用采样节点邻域的聚合观测值去重构信号,更适用于存在聚集性质的图结构。图子集选取则从图节点集中采样最具有信息量的节点子集,将这些节点的(带噪)信号值作为观测值去重构原始信号,可应用于多个领域,如环境监测[15]、半监督节点分类[16]、矩阵补全[17]等。

由于图结构具有离散性质,图子集选取本质是一个组合优化问题,已被证明为NP难[18],可以近似求解。现有方法可以归为两类：(1)随机算法;(2)确定性算法[19]。前者通过在图节点集上定义一个概率分布函数,依据分布随机地采样节点[6-8]。后者则通过优化预先定义的损失函数,寻找最优采样集[9-14]。研究表明,在采样点数相同的情况下,随机算法的重构效果很难超过确定性算法[7]。虽然确定性算法效果更优,现有方法大多从谱域设计优化准则,并未考虑节点域内采样集节点的距离关系,而在平滑假设下,采样距离相近的点对重构效果带来的增益可能十分有限。同时,这类算法通常使用贪心优化,即每一步迭代时,选择最大化或最小化目标函数的局部最优点。然而,贪心方法可能会陷入局部最优解,并不能保证全局最优,并且由于采样点的选择依赖前序已采样节点,采样只能串行执行,在处理大规模图时效率较低。

针对以上不足,该文提出以图割(Graph Cut) 的视角建模图子集选取问题,既考虑了采样集节点在节点域和谱域的信息,又可实现一次性采样,并行运行。具体地,首先利用局部算子构建一个新的内积完全图,再利用谱聚类算法生成标准图割,得到节点集的划分,使得同一子集内的节点距离尽可能近,不同子集间的节点距离足够远;其次,在每个子集内依据稀疏性度量采样最优节点,即可组成最终的采样集。在多种图上的实验结果表明,提出的算法(Cut Sampling)优于现有文献中的几种代表性算法。

该文的贡献总结如下：

(1)提出利用图割为图子集选取划分采样可行集,利用局部算子构建内积完全图,可控制采样集节点的间隔距离,同时结合了谱域的局部性;

(2)提出的算法不需要贪心优化,可以在采样步骤并行运行,具有可扩展性;

(3)相比于几种现有文献中的代表性算法,提出的方法实验效果更优或相近。

1 相关研究

现有的图子集选取方法可分为两类：随机算法和确定性算法。随机算法根据定义的概率分布在节点集随机采样从而生成采样集。研究表明,独立于图结构的均匀分布,当采样足够多个节点时,对于Erdös-Rényi图(ER图)可高概率实现完美重构[1],而非均匀的随机采样则根据基于图结构的节点重要性设计概率分布[7-8]。虽然与图结构无关的随机采样计算高效,利用压缩感知中约束等距性质(Restricted Isometry Property,RIP)的理论研究表明,在采样点数相同的情况下,与图结构相关的随机采样方法效果更优[7],文献[6]展示了具体对比。同时,随机方法很难保证采样集中的节点距离足够远,而在图信号的平滑假设下,距离相近的采样点带来的信息增益可能有限[12]。故该文沿确定性算法展开研究。

确定性算法大多为谱方法,通过松弛优化[20]或贪心优化去最大化或最小化某种定义的损失函数。例如基于实验设计的优化准则,E-optimal[1],A-optimal和D-optimal[9]等。虽然这类贪心算法通常可以获得较好的重构效果,但依赖特征分解,计算复杂度较高。为避免特征分解,可以对谱域优化准则做近似处理,如MaxCutoff[10]利用图谱代理 (Graph Spectral Proxies),去近似最大化截止频率;Fen Wang等[21]利用诺伊曼级数(Neumann Series)优化A-optimal准则等。另有一些方法虽无法避免准备工作阶段的特征分解,但将贪心算法中加入一个节点后比较全局指标,转换为利用每个节点的增量误差衡量节点质量,可以避免节点选择步骤的特征分解,如利用QR分解[13],借鉴压缩感知中正交匹配追踪算法的思路,通过投影算子定义残差[14]等。但上述方法大多只实现了频域内采样的局部性,并没有考虑图拓扑结构以及采样节点的空间关系。还有些确定性算法只考虑节点域信息,如传感器设置方法[22],可有效避免对图傅里叶基的依赖。

近年来,结合谱域与节点域信息的方法被相继提出[11-12],Jayawant等[11]提出一个两步算法,首先寻找和已采样节点距离足够远的节点可行集,其次在可行集内根据准则贪心寻找最优点。Sakiyama等[12]想法类似,利用定义在节点域的局部算子[23]合并上述两步,提出Ed Free算法。同时,Sakiyama等还证明了许多确定性算法可用局部算子统一表示。但是这些算法同样使用贪心优化去一个个选择最优节点,串行采样,效率较低。鉴于结合节点域与谱域的图子集选取方法展示出优秀的节点选择能力,同时考虑到局部算子的泛化性及其可以结合两域信息的特性,该文沿用局部算子并从节点距离出发,提出用新的视角图割[24]去建模图子集选取问题,可在一定程度上克服现有谱域贪心算法的不足。

2 预备知识

2.1 图信号处理

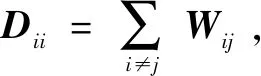
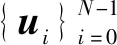
(1)

GFT之所以可利用LG的特征分解定义,可以从LG的二次型理解,它可表示为图上有边相连的节点信号值变化的加权平方和,反映了图信号的平滑程度。

(2)

将ui视为图上的信号,则当λi越小,ui会越平滑。传统离散信号处理中,随时间变化越缓慢的信号频率越低,类似地,沿图中边变化越平滑的图信号频率越低,因此GFT可将特征值看作信号的频率,低频代表图信号沿边的变化平滑,高频代表变化剧烈。

在图信号处理中,通常假设图信号满足基于图结构的某些条件,例如平滑、带限等。该文研究带限图信号,定义如下：

(3)

局部算子(Localization Operators)是传统信号处理中的平移算子在图信号处理领域的拓展,可以同时结合节点域和谱域信息,定义如下：

定义2(局部算子[23])：∀n∈{0,1,…,N-1},节点i∈V处局部算子的第n个分量元素定义如下：

(4)

其中,(*)表示图卷积,g为谱域核,δi为节点i处的脉冲信号。局部算子的矩阵形式如下：

Tg=[Tg,0,Tg,1,…,Tg,N-1]=

(5)

常用谱域核有热核g(λi)=e-πλi,此时Tg,i具有围绕节点i移动窗口的作用[23]。另一常用的为理想核,当i

2.2 问题形式

图子集选取问题可分为两步：采样和重构。假设想要找到一个大小为M的采样集M⊆V,其中M=(M0,M1,…,MM-1)表示采样序列,并且 Mi∈{0,1,…,N-1}是非重复的。只有采样节点的信号值是可以观测到的。采样矩阵Ψ：RNRM定义如下：

(6)

令w∈RM为观测中引入的噪声,假设服从i.i.d.高斯分布,则采样信号为xM=Ψx,观测模型为yM=Ψx+w,对于带限图信号,观测模型可写作：

(7)

当采样集M固定后,真实信号值可由最优线性估计(Best Linear Unbiased Estimation)[25]重构得到：

(8)

2.3 图 割

图割是对图节点集的划分,标准图割(Normalized Graph Cut,N-CUT)是一类经典的图割,通常具有优秀的聚类效果,其定义如下：

定义3(标准图割(N-CUT)[24])：图G=(V,ε,W)大小为M的标准图割为节点集V的一个分割{A1,A2,…,AM},使得下式目标函数最小化。

(9)

N-CUT通常作用于相似性图,用于将节点集划分为多个簇,使得簇间节点具有低相似度,簇内节点具有高相似度。这是一个NP难问题,可以用谱聚类算法放缩求解[26]。

3 Cut Sampling算法介绍

3.1 信号重构

由公式(8),利用带理想核的局部算子,重构信号可表示为局部算子的加权线性组合形式：

TVM(TMM)†yM=

(10)

其中,c=(TMM)†yM。

由于信号重构本质是利用采样值去插值估计未观测值,由公式(10),未观测节点的值亦可以由采样节点处Tg,i的带权线性组合插值得到。故Tg,i的非零分量,即覆盖区域,可被视作节点i对重构信号有贡献的节点区域。为使得重构误差尽可能小,最优采样集应具有尽可能大的覆盖区域,即单个采样节点的覆盖区域尽可能大,同时,采样节点间的覆盖区域交集尽可能小。

具体地,‖Tg,i‖1可表示节点i的信号覆盖域,内积〈|Tg,i|,|Tg,j|〉可代表节点i和j信号覆盖区域的交集大小。例如,若〈|Tg,i|,|Tg,j|〉=0,则表示节点i和j的信号覆盖域无交集。

基于上述性质,该文利用局部算子的内积构建一张完全图,边权为信号覆盖域交集大小的度量,并在此基础上提出一个两步的图子集选取算法Cut Sampling：(1)N-CUT聚类;(2)在每个子集内根据稀疏性准则选择最优点。

完整算法流程如图1所示。

图1 Cut Sampling算法流程

3.2 图割聚类

对于原始图G=(V,ε,W),算法首先通过构建一个对应的完全图Q=(V,ε'),以边权去度量图上任意两个节点的空间距离关系。具体地,图Q中的边权为相连两个节点的局部算子的内积。

(11)

由前述局部算子的性质可知,图Q即为原始图中节点距离的度量图,可通过求解N-CUT将节点集按节点的距离关系划分为指定个数簇。由公式(9),图Q的N-CUT的最小化目标函数可写作：

(12)

算法1：N-CUT谱聚类算法[26]。

输入：距离图Q=(V,ε'),采样个数M,特征向量矩阵U;

输出：节点子集{S1,S2,…,SM}。

1.取U的前M列的第i行,zi=UiM∈RM,∀i∈{0,1,…,N-1};

3.3 簇内采样

图割步骤为后续采样划分了可行集范围。由于图割已控制不同子集间的点距离足够远,为了选出最具信息量的采样集,算法Cut Sampling第二步在各子集Si内分别选取最有代表性的点,共同组成最终的采样集。具体地,定义如下采样准则,其中Tg,j表示节点j处的局部算子：

(13)

Ed Free[12]中利用了局部算子的1范数,而最大化1范数等价于寻找覆盖域最大的信号节点。该文在此基础上增加了分母对2范数的限制,这也是一种稀疏性度量[8]。从信号重构的角度不难理解,由于信号重构本质是对观测值的插值,过于稀疏的局部算子代表当前节点可能与其他节点有较小的关联,不具有代表性,可能带来较大的重构误差。算法希望采样信号在具有较大覆盖域的同时,不会过于稀疏,即避免非零分量过于集中导致难以提供足够信息。例如,假设Tg,1=[1,0,0,…,0],Tg,2=[1/2,1/2,0,…,0],则Tg,1和Tg,2的1范数均为1,但Tg,2的2范数更小。由公式(13),该文的采样准则将选择Tg,2而非更稀疏的Tg,1。完整算法总结如算法2所示。

算法2：Cut Sampling算法。

输入：图G=(V,ε,W),采样个数M,特征向量矩阵UVK,局部算子Tg;

输出：采样集M⊆V,|M|=M。

3.在各节点子集Si中,选择最优节点,∀i=1,2,…,M;

4 数值实验

4.1 实验设置

实验利用GSPBOX[27],在如下四类图上对比不同算法的重构效果：

(1)随机Sensor图：为带权稀疏图;

(2)Minnesota交通图：为等权重图,边权均为1;

(4)基于Erdös-Rényi模型的随机图(ER 图)：边的连接概率p分别设置为0.05、0.15和0.5。

将Cut Sampling与下列三种方法进行比较：

(1)随机采样[7]：概率分布为均匀的;

(2)MinSpec[1]：确定性算法,贪心优化E-Optimal准则,每次迭代需特征分解;

(3)Ed Free[12]：确定性算法,无需特征分解,利用局部算子,考虑了节点间的空间关系。

Cut Sampling与Ed Free算法中的局部算子均使用热核函数g(λ)=e-aλ,其中a=vpepmpk/λmax,v∈R+为可调参数,设置为75,pe=|ε|/N为连边概率,pm=M/N为采样比例,pk=K/N为带宽。

4.2 采样集比较

图2展示了N=500的Sensor图上四种算法的采样结果,圈出节点构成采样集,大小为M=15。如图2(a)和图2(b),随机采样和MinSpec生成的采样集中,节点距离可能很近,分布并不均匀。这两种方法在采样时,随机或根据谱域准则优化,并未考虑图的拓扑结构与节点间的位置关系,这也导致了较大的重构误差。Ed Free和Cut Sampling在采样时都考虑了节点的位置关系,最终的采样集分布较为均匀,采样节点间保持了一定距离,如图2(c)和图2(d)所示。同时,这两种方法都利用了局部算子,可以观察到采样集有部分重合。

图2 随机Sensor图的采样节点集

4.3 重构误差比较

图3展示了四种图场景下,四种算法的重构误差随采样集大小的变化。实验通过计算重构信号与原始信号的均方误差(Mean Squared Error,MSE)来评价重构效果。为了获得相对稳定的实验结果,对于每张图,实验均生成100次信号,并取均方误差的平均值。评价指标如下：

图3 重构误差MSE随采样集大小M的变化(平均100次)

(14)

其中,x'表示重构信号。

实验结果表明,该算法在几乎所有场景下重构效果最优,算法在四种图上都取得了最小或与其他方法接近的重构误差。特别地,在Sensor图和Minnesota图上,Cut Sampling稳定优于其他三种方法。对于BA图,当采样集足够大时,Cut Sampling效果更好。对于ER图,当连边的概率较小时,Cut Sampling重构效果接近其他方法,随着连边概率提高,Cut Sampling相比于Ed Free的提升也明显增加。

同时,可以观察到,对于考虑了图拓扑结构的Cut Sampling和Ed Free,这两种方法的重构表现基本优于没有考虑节点位置关系的随机采样和MinSpec,特别是在Sensor图和Minnesota图上。这也反映了将图拓扑信息与频域信息相结合,可有效提高采样算法的重构效果。

5 结束语

该文提出了一种两步图子集选取方法,先图割聚类,再簇内采样。首先利用局部算子的内积生成一张度量节点空间距离的完全图,再利用谱聚类算法求解该图的N-CUT,得到节点集依距离的划分。最后,在各个子集内,根据局部算子的稀疏性准则,分别选择最优点,组成最终的采样集。相比于大多数谱域算法,该方法结合了顶点域的空间信息去控制采样集内节点的距离,使得采样集分布相对均匀。同时,区别于常见的贪心优化框架,该文利用图割实现采样步骤可以并行选择全部节点,具有一定可扩展性。在多种图场景下与多种代表性算法相比,该方法能达到最优或接近的效果。

考虑到谱聚类算法的计算复杂度较高,如何更加高效准确的聚类是未来的一个研究方向。同时,对该算法进一步的理论分析也是未来工作之一。