面向多任务的频谱感知博弈算法
郭晓敏,朱 琦
(南京邮电大学 江苏省无线通信重点实验室,江苏 南京 210003)
0 引 言
无线电频谱是一种稀缺资源,伴随5G通信网络的出现,用户对于频谱资源的需求急剧增加,如何缓解频谱资源紧缺的现状是急需解决的现实问题[1]。认知无线电(Cognitive Radio,CR)是提高频谱资源利用率的有效方案,通过认知无线电中的频谱感知技术检测授权用户(Authorized User,AU)合法使用但未被占用的空闲频谱,并将其分配给有需要的次用户(Second User,SU),实现频谱共享,可以有效解决频谱利用率低的问题[2]。目前,在认知无线电领域中频谱感知依旧是非常重要的研究方向。比如在很多行业,无人机由于它的多功能性而备受青睐,但是面对频谱资源贫乏的现状,无人机可用的频谱资源严重受限,一种可行的解决方案就是利用频谱感知技术增加无人机可使用的频段,从而解决无人机频谱资源短缺的问题[3-5]。
在频谱感知领域的研究工作有很多:文献[6]提出一种新的频谱感知策略,采用宽频带感知的方式搜索AU未占用频带,最小化感知时间,最大化整体吞吐量;文献[7]提出一种新的基于对抗学习的频谱感知方法来提高模型对新信噪比值的适应性,在训练信噪比集中提取通用的不依赖于信噪比的特征,并利用这些特征推断新的测试信噪比集中的频谱状态,该方法可以降低频谱感知错误率;文献[8]在多种机器学习算法的基础上,提出一种新的频谱感知算法,通过识别AU发射器的发射模式,在最大限度减少对AU的影响的前提下获得授权频谱上用户行为的了解,提高次用户接入频谱的机会。
以上研究工作都是在频谱感知领域进行的,目前也已经有一些研究将频谱感知与激励机制结合:文献[9]设计一种基于契约理论的激励机制,契约理论将基站与SU之间的交互建模为劳动力市场,基站作为买家在不知道卖家(SU)隐私信息的情况下,通过支付报酬的形式鼓励他们积极参与频谱感知,基站选择信噪比高的次用户,将他们的检测概率进行融合得到检测结果;文献[10]提出一种基于声誉的激励机制,每个SU会给与他相邻的SU进行声誉评估,向融合中心报告检测概率的时候会将评估结果一同报告过去,融合中心根据每个SU提交的检测概率和周围SU对他的评估更新他的声誉,有效减少恶意次用户为了获得更高报酬虚假汇报的影响;文献[11]提出了一种基于SU分类的协作频谱感知算法,引入激励机制来鼓励更多的SU积极参与检测,该算法根据信道条件将次用户分为普通次用户(OSU)和中继次用户(RSU)。首先,每个SU通过计算效用函数决定是否参与,然后,OSU将检测到的数据发送给附近的RSU,接着,RSU将收到的数据与本地检测数据一同传送给融合中心。
上述研究虽然将频谱感知与激励机制结合,但都是针对单个频段进行频谱感知,在实际系统中,往往需要占用多个频段。该文将群智感知技术引入到频谱感知中,考虑次用户分类的场景,提出了一种面向多任务的频谱感知博弈算法。
该算法将感知需求次用户向协作感知次用户支付报酬的问题建模为斯坦克尔伯格博弈模型,其中感知需求次用户是博弈模型中的领导层,协作感知次用户是博弈模型中的从属层。在领导层博弈中,综合考虑检测概率和报酬定义了感知需求次用户的效用,通过博弈优化报酬以获得最佳效用;在从属层博弈中,综合考虑检测概率和感知时间,定义了协作感知次用户的效用,根据感知需求次用户发布的报酬通过优化感知时间以获得最佳效用,并且推导证明了感知时间的优化存在纳什均衡。通过仿真分析,该算法有效提高了协作感知次用户的频谱感知性能。
1 系统模型
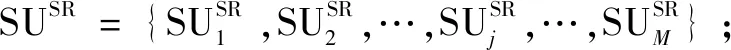
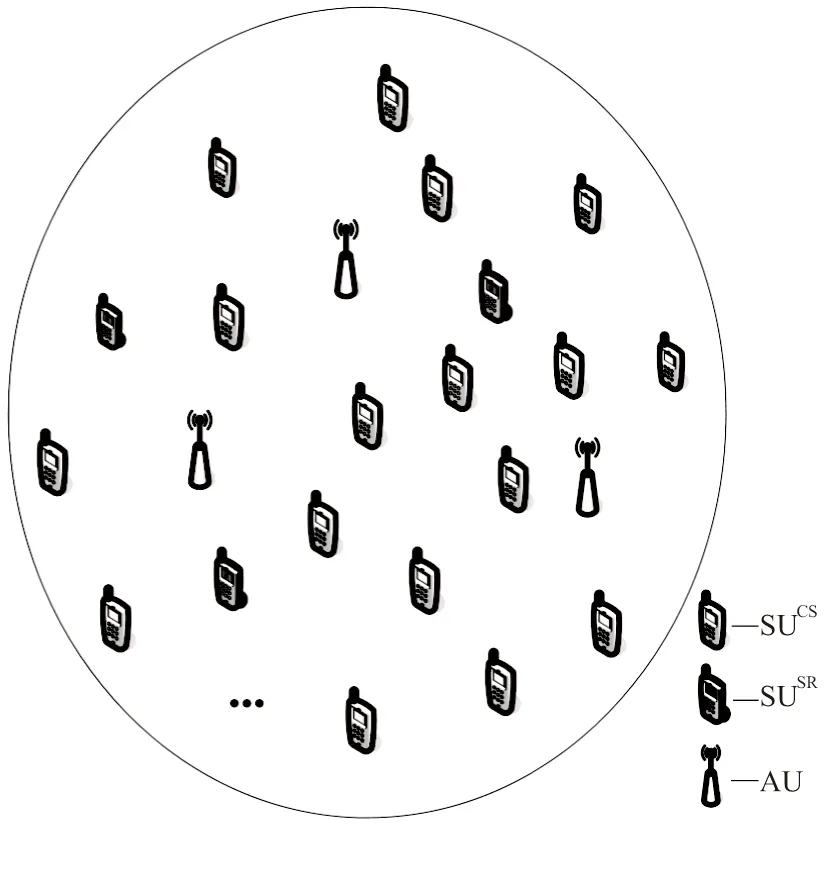
图1 系统模型
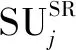

表1 符号含义
2 多任务频谱感知博弈算法
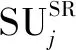
2.1 博弈模型
感知需求次用户效用优化问题和协作感知次用户效用优化问题共同构成了一个斯坦克尔伯格博弈,博弈的目标是找到斯坦克尔伯格均衡。斯坦克尔伯格均衡被定义为一个稳定点,在这个稳定点上从属层做出最佳策略选择并且使领导层的收益最大化。具体将斯坦克尔伯格均衡定义如下:
定义(斯坦克尔伯格均衡):假设t*表示协作感知次用户(从属层)的最佳感知时间策略,B*表示感知需求次用户(领导层)的最佳奖励策略。假设ti表示协作感知次用户i的策略,t-i表示除了协作感知次用户i以外所有协作感知次用户的策略,Bj表示感知需求次用户j的策略,B-j表示除了感知需求次用户j以外其他感知需求次用户的策略。因此,斯坦克尔伯格均衡点(t*,B*)满足以下条件:
Πj(Bj*,B-j*,t*)≥Πj(Bj,B-j*,t*),∀j,
(1)
以及,
(2)
其中,t=[t1,t2,…,tN]T,B=[B1,B2,…,BM]T。
2.2 领导层博弈
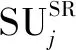
(3)
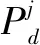
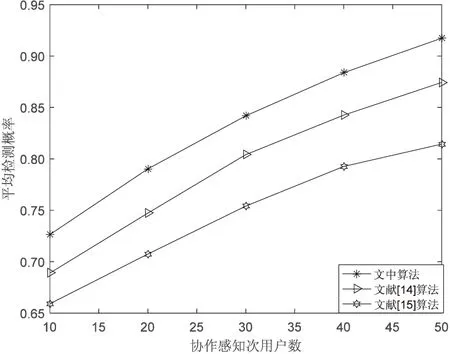
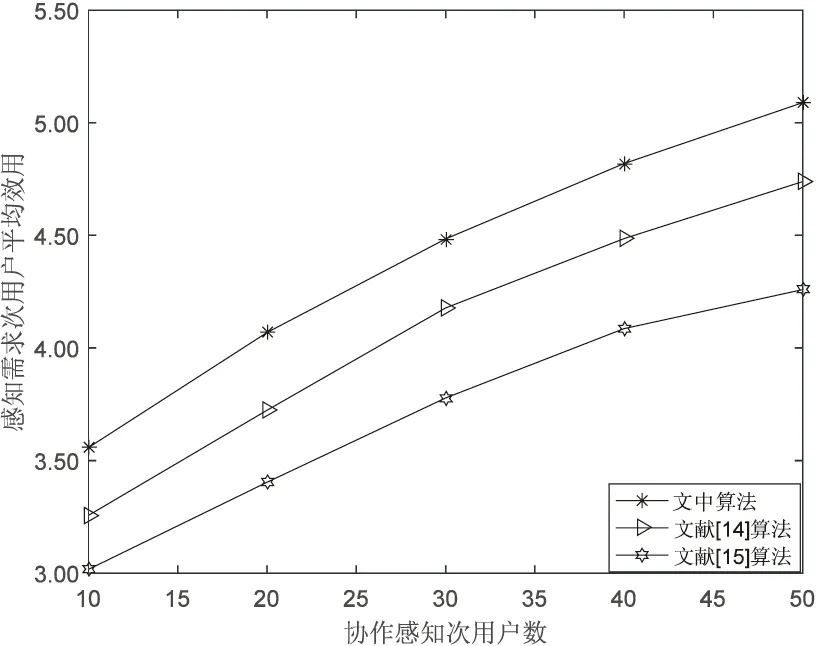
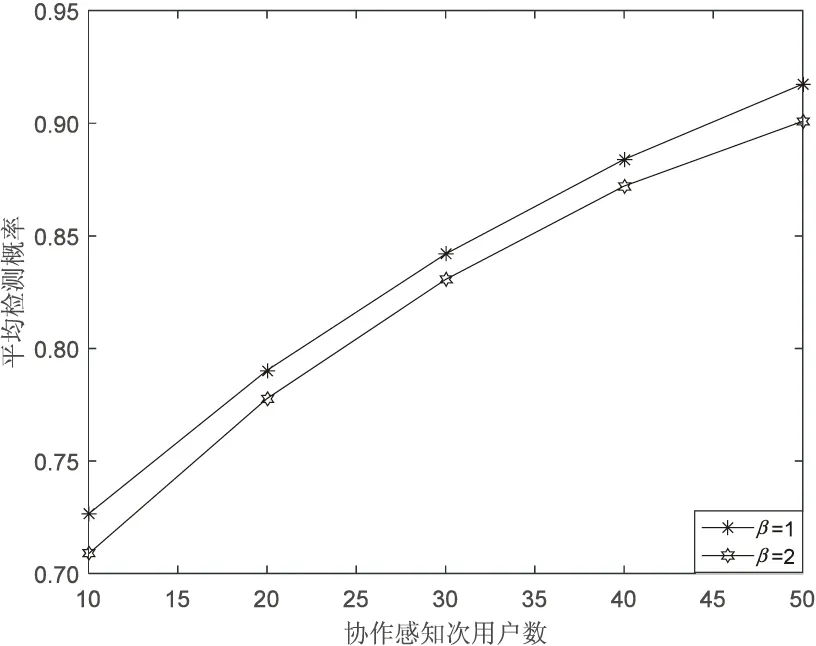
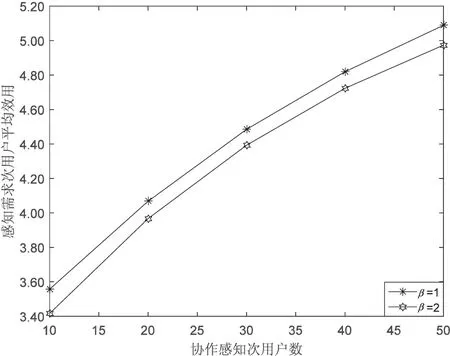
0 (4) 算法1:感知需求次用户博弈算法。 3:times=1 4:While(1) 11:end if 13:times=times+1 14:repeat 3~10 16:end while (5) cij=β×tij+γ×dij (6) 其中,β和γ表示加权系数。 Uij(tij)=pij-cij= (7) (8) 在认知无线电频谱感知中,SU通过能量检测法来感知AU的频谱是否在使用,协作感知次用户i感知频段j的检测概率公式表示为[12]: (9) 其中,pf表示次用户i的虚警概率,γij表示次用户i感知频段j的信噪比,tij表示次用户i感知频段j的感知时间,fs表示采样频率,通常是一个定值,Q函数是一个互补的累积分布函数,表达式为: (10) 每个感知需求次用户采用表决融合准则对多个协作感知次用户提交的感知结果进行处理,经过表决融合后感知任务j的检测概率分别表示为[13]: 进而,Uij关于tij的一阶偏导数表示为: 进而,Uij关于tij的二阶偏导数表示为: (14) 其中: (15) 对K'进一步推导分解可得: 即Uij关于tij的一阶偏导数存在正值。 假设当K→-∞时,可得tij→∞,从而有: (17) 算法2:协作感知次用户博弈算法。 1:forj=1:M 2:fori=1:N 4:end for 5:end for 6:根据完成感知任务消耗的成本产生一个报价bij 算法3:群智频谱感知算法。 1:repeat 10:repeat 1~9 该文采用MATLAB对算法进行仿真,仿真场景如图1所示。在一个半径为200米的圆中,随机分布着N个协作感知次用户和M个感知需求次用户,该文取M=2。协作感知次用户的采样频率取200 MHz,虚警概率取0.1,加权系数α=8,β=1,γ=0.3[12],无线信号传输考虑大尺度衰落,并且衰落系数取4,表决融合准则的判决门限值取N/2。将提出的算法与文献[14-15]中的算法进行对比分析,文献[14-15]中协作感知次用户的感知时间没有博弈,不做优化,协作感知次用户的效用是报酬减去成本。文献[14]中报酬根据每个协作感知次用户的感知时间与该任务总感知时间的占比分配获得,文献[15]中采用的是拍卖,报酬根据每个协作感知次用户的报价获得。 该文选取融合后检测概率的平均值、感知需求次用户效用的平均值、协作感知次用户效用的平均值,即平均检测概率,感知需求次用户的平均效用、协作感知次用户的平均效用作为评价指标,通过仿真图描述不同评价指标随协作感知次用户数量变化的情况来展示算法性能。 图2 平均检测概率 图3 感知需求次用户的平均效用 图4 不同β值情况下的平均检测概率 图5描述了在不同β取值时,感知需求次用户的平均效用和协作感知次用户数量之间的关系。根据SUSR的效用可知,检测概率与支付协作感知次用户的报酬都可以影响其效用,并且前者对效用的影响更大。从图5中可以看出,随着SUCS数量的增加,SUSR的效用会增加,这是由于随着SUCS数量的增加,SUSR的检测概率也会增加,SUSR得到的效用就会随之变大,从而SUSR的平均效用变大。同时从图5中可以看出,β的值越大,SUSR的效用越低,这是因为β的值越大,单个感知次用户的检测概率越低,经过表决融合后的检测概率越小,SUSR的效用越低,从而感知需求次用户的平均效用越低。 图5 不同β值情况下的感知需求次用户平均效用 频谱资源紧缺的问题日益显著,认知无线电技术的诞生缓解了这个问题,通过频谱共享大大提高了频谱利用率。频谱感知是认知无线电的关键技术。次用户的检测概率与感知时间有关,感知时间短的次用户检测概率低。为了提升频谱感知的准确性,该文将群智感知技术引入频谱感知中,提出了一种面向多任务的频谱感知博弈算法。该算法将感知需求次用户向协作感知次用户支付报酬的问题建模为Stackelberg博弈模型,其中感知需求次用户是博弈模型中的领导层,协作感知次用户是博弈模型中的从属层。在领导层博弈中,综合考虑检测概率和报酬定义了感知需求次用户的效用,通过博弈优化报酬以获得最佳效用;在从属层博弈中,综合考虑检测概率和感知时间定义了协作感知次用户的效用,根据感知需求次用户发布的报酬通过优化感知时间以获得最佳效用,并且推导证明了感知时间的优化存在纳什均衡。仿真结果表明,该算法可以提高协作频谱感知的检测概率。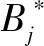
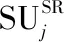
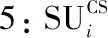

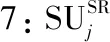
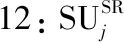
2.3 从属层博弈
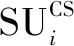
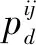
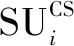
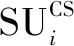
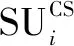
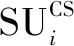
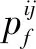
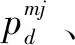
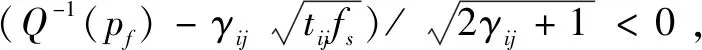
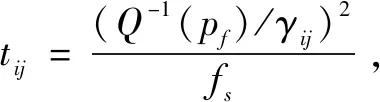
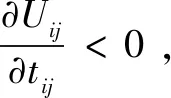
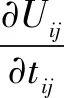
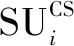
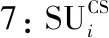
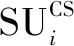
2.4 算法步骤
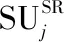
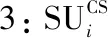
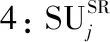
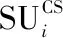
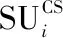
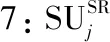
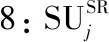
3 仿真结果与分析


4 结束语

